Published online by Cambridge University Press: 31 August 2012
Thurston introduced 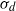 $\sigma _d$-invariant laminations (where
$\sigma _d$-invariant laminations (where 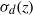 $\sigma _d(z)$ coincides with
$\sigma _d(z)$ coincides with 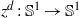 $z^d:\mathbb S ^1\to \mathbb S ^1$,
$z^d:\mathbb S ^1\to \mathbb S ^1$, 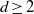 $d\ge 2$) and defined wandering
$d\ge 2$) and defined wandering 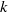 $k$-gons as sets
$k$-gons as sets 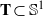 ${\mathbf {T}}\subset \mathbb S ^1$ such that
${\mathbf {T}}\subset \mathbb S ^1$ such that 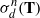 $\sigma _d^n({\mathbf {T}})$ consists of
$\sigma _d^n({\mathbf {T}})$ consists of 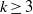 $k\ge 3$ distinct points for all
$k\ge 3$ distinct points for all 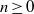 $n\ge 0$ and the convex hulls of all the sets
$n\ge 0$ and the convex hulls of all the sets 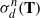 $\sigma _d^n({\mathbf {T}})$ in the plane are pairwise disjoint. He proved that
$\sigma _d^n({\mathbf {T}})$ in the plane are pairwise disjoint. He proved that 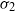 $\sigma _2$ has no wandering
$\sigma _2$ has no wandering 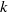 $k$-gons. Call a lamination with wandering
$k$-gons. Call a lamination with wandering 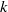 $k$-gons a WT-lamination. In a recent paper, it was shown that uncountably many cubic WT-laminations, with pairwise non-conjugate induced maps on the corresponding quotient spaces
$k$-gons a WT-lamination. In a recent paper, it was shown that uncountably many cubic WT-laminations, with pairwise non-conjugate induced maps on the corresponding quotient spaces 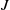 $J$, are realizable as cubic polynomials on their (locally connected) Julia sets. Here we use a new approach to construct cubic WT-laminations with the above properties so that any wandering branch point of
$J$, are realizable as cubic polynomials on their (locally connected) Julia sets. Here we use a new approach to construct cubic WT-laminations with the above properties so that any wandering branch point of 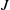 $J$ has a dense orbit in each subarc of
$J$ has a dense orbit in each subarc of 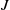 $J$ (we call such orbits condense), and show that critical portraits corresponding to such laminations are dense in the space
$J$ (we call such orbits condense), and show that critical portraits corresponding to such laminations are dense in the space 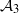 ${\mathcal A}_3$of all cubic critical portraits.
${\mathcal A}_3$of all cubic critical portraits.