No CrossRef data available.
Published online by Cambridge University Press: 01 June 2015
Suppose that 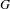 $G$ is a compact Abelian topological group,
$G$ is a compact Abelian topological group, 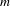 $m$ is the Haar measure on
$m$ is the Haar measure on 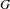 $G$ and
$G$ and  $f:G\rightarrow \mathbb{R}$ is a measurable function. Given
$f:G\rightarrow \mathbb{R}$ is a measurable function. Given  $(n_{k})$, a strictly monotone increasing sequence of integers, we consider the non-conventional ergodic/Birkhoff averages
$(n_{k})$, a strictly monotone increasing sequence of integers, we consider the non-conventional ergodic/Birkhoff averages 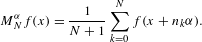 $$\begin{eqnarray}M_{N}^{\unicode[STIX]{x1D6FC}}f(x)=\frac{1}{N+1}\mathop{\sum }_{k=0}^{N}f(x+n_{k}\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
$$\begin{eqnarray}M_{N}^{\unicode[STIX]{x1D6FC}}f(x)=\frac{1}{N+1}\mathop{\sum }_{k=0}^{N}f(x+n_{k}\unicode[STIX]{x1D6FC}).\end{eqnarray}$$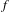 $f$-rotation set is
$f$-rotation set is 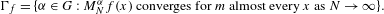 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{f}=\{\unicode[STIX]{x1D6FC}\in G:M_{N}^{\unicode[STIX]{x1D6FC}}f(x)\text{ converges for }m\text{ almost every }x\text{ as }N\rightarrow \infty \}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{f}=\{\unicode[STIX]{x1D6FC}\in G:M_{N}^{\unicode[STIX]{x1D6FC}}f(x)\text{ converges for }m\text{ almost every }x\text{ as }N\rightarrow \infty \}.\end{eqnarray}$$
We prove that if 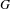 $G$ is a compact locally connected Abelian group and
$G$ is a compact locally connected Abelian group and  $f:G\rightarrow \mathbb{R}$ is a measurable function then from
$f:G\rightarrow \mathbb{R}$ is a measurable function then from  $m(\unicode[STIX]{x1D6E4}_{f})>0$ it follows that
$m(\unicode[STIX]{x1D6E4}_{f})>0$ it follows that 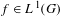 $f\in L^{1}(G)$. A similar result is established for ordinary Birkhoff averages if
$f\in L^{1}(G)$. A similar result is established for ordinary Birkhoff averages if 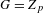 $G=Z_{p}$, the group of
$G=Z_{p}$, the group of  $p$-adic integers. However, if the dual group,
$p$-adic integers. However, if the dual group, 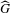 $\widehat{G}$, contains ‘infinitely many multiple torsion’ then such results do not hold if one considers non-conventional Birkhoff averages along ergodic sequences. What really matters in our results is the boundedness of the tail,
$\widehat{G}$, contains ‘infinitely many multiple torsion’ then such results do not hold if one considers non-conventional Birkhoff averages along ergodic sequences. What really matters in our results is the boundedness of the tail, 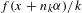 $f(x+n_{k}\unicode[STIX]{x1D6FC})/k$,
$f(x+n_{k}\unicode[STIX]{x1D6FC})/k$, 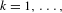 $k=1,\ldots ,$ for almost every
$k=1,\ldots ,$ for almost every  $x$ for many
$x$ for many  $\unicode[STIX]{x1D6FC}$; hence, some of our theorems are stated by using instead of
$\unicode[STIX]{x1D6FC}$; hence, some of our theorems are stated by using instead of 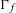 $\unicode[STIX]{x1D6E4}_{f}$ slightly larger sets, denoted by
$\unicode[STIX]{x1D6E4}_{f}$ slightly larger sets, denoted by 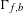 $\unicode[STIX]{x1D6E4}_{f,b}$.
$\unicode[STIX]{x1D6E4}_{f,b}$.