Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T09:45:32.059Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of the Peierls barrier and robustness of laminations

Published online by Cambridge University Press:  13 March 2014

BLAŽ MRAMOR  and
BOB RINK
BLAŽ MRAMOR
Affiliation:
Institute of Mathematics, Albert-Ludwigs-Universität, Freiburg, Germany email [email protected]
BOB RINK
Affiliation:
Department of Mathematics, VU University Amsterdam, The Netherlands email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the Peierls barrier 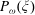$P_{\omega }(\xi )$ for a broad class of monotone variational problems. These problems arise naturally in solid state physics and from Hamiltonian twist maps. We start by deriving an estimate for the difference 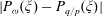$\vert P_{\omega }(\xi ) - P_{q/p}(\xi ) \vert $ of the Peierls barriers of rotation numbers 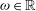$\omega \in {{\mathbb{R}}}$ and 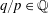$q/p\in {\mathbb{Q}}$. A similar estimate was obtained by Mather [Modulus of continuity for Peierls’s barrier. Proc. NATO Advanced Research Workshop on Periodic Solutions of Hamiltonian Systems and Related Topics (Il Ciocco, Italy, 13–18 October 1986) (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 209). Eds. P. H. Rabinowitz, A. Ambrosetti and I. Eckeland. D. Reidel, Dordrecht, 1987, pp. 177–202] in the context of twist maps, but our proof is different and applies more generally. It follows from the estimate that 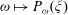$\omega \mapsto P_{\omega }(\xi )$ is continuous at irrational points. Moreover, we show that the Peierls barrier depends continuously on parameters and hence that the property that a monotone variational problem admits a lamination of minimizers of rotation number 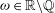$\omega \in {{\mathbb{R}}}\delimiter "026E30F {\mathbb{Q}}$ is open in the 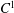$C^1$-topology.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1263 - 1288
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angenent, S. B.. Monotone recurrence relations, their Birkhoff orbits and topological entropy. Ergod. Th. & Dynam. Sys. 10(1) (1990), 15–41.CrossRefGoogle Scholar
Aubry, S. and Le Daeron, P. Y.. The discrete Frenkel–Kontorova model and its extensions. I. Exact results for the ground-states. Phys. D 8(3) (1983), 381–422.CrossRefGoogle Scholar
Aubry, S., MacKay, R. S. and Baesens, C.. Equivalence of uniform hyperbolicity for symplectic twist maps and phonon gap for Frenkel–Kontorova models. Phys. D 56(2–3) (1992), 123–134.CrossRefGoogle Scholar
Bangert, V.. A uniqueness theorem for $\mathbb{Z}^n$ periodic variational problems. Comment. Math. Helv. 62(4) (1987), 511–531.CrossRefGoogle Scholar
Calleja, R. and de la Llave, R.. A numerically accessible criterion for the breakdown of quasi-periodic solutions and its rigorous justification. Nonlinearity 23(9) (2010), 2029–2058.CrossRefGoogle Scholar
de la Llave, R. and Valdinoci, E.. Critical points inside the gaps of ground state laminations in statistical mechanics. J. Stat. Phys. 129(1) (2007), 81–119.Google Scholar
de la Llave, R. and Valdinoci, E.. Ground states and critical points for Aubry–Mather theory in statistical mechanics. J. Nonlinear Sci. 20(2) (2007), 153–218.CrossRefGoogle Scholar
Forni, G.. Analytic destruction of invariant circles. Ergod. Th. & Dynam. Sys. 14(2) (1994), 267–298.CrossRefGoogle Scholar
Golé, C.. Symplectic Twist Maps: Global Variational Techniques (Advanced Series in Nonlinear Dynamics, 18). World Scientific, Singapore, 2001.Google Scholar
Koch, H., de la Llave, R. and Radin, C.. Aubry–Mather theory for functions on lattices. Discrete & Contin. Dynam. Sys. 3(1) (1997), 135–151.CrossRefGoogle Scholar
MacKay, R. S. and Percival, I. C.. Converse KAM: theory and practice. Comm. Math. Phys. 98(4) (1985), 469–512.CrossRefGoogle Scholar
Mather, J. N.. Existence of quasiperiodic orbits for twist homeomorphisms of the annulus. Topology 21(4) (1982), 457–467.CrossRefGoogle Scholar
Mather, J. N.. Modulus of continuity for Peierls’s barrier. Proc. NATO Advanced Research Workshop on Periodic Solutions of Hamiltonian Systems and Related Topics (Il Ciocco, Italy, 13–18 October 1986) (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 209). Eds. P. H. Rabinowitz, A. Ambrosetti and I. Eckeland. D. Reidel, Dordrecht, 1987, pp. 177–202.CrossRefGoogle Scholar
Mather, J. N.. Destruction of invariant circles. Ergod. Th. & Dynam. Sys. 8* (Charles Conley Memorial Issue) (1988), 199–214.Google Scholar
Mather, J. N. and Forni, G.. Action minimizing orbits in Hamiltonian systems. Transition to Chaos in Classical and Quantum Mechanics (Proceedings of a CIME Summer School, 6–13 July 1991) (Lecture Notes in Mathematics, 1589). Ed. Graffi, S.. Springer, Berlin, 1994, pp. 92–186.CrossRefGoogle Scholar
Moser, J.. Minimal solutions of variational problems on a torus. Ann. Inst. Henri Poincaré 3(3) (1986), 229–272.CrossRefGoogle Scholar
Moser, J.. A stability theorem for minimal foliations on a torus. Ergod. Th. & Dynam. Sys. 8* (Charles Conley Memorial Issue) (1988), 251–281.Google Scholar
Moser, J.. Minimal foliations on a torus. Topics in the Calculus of Variations (Lectures given at the 2nd 1987 Session of the Centro Internazionale Matematico Estivo—CIME, Montecateni Terme, Italy) (Lecture Notes in Mathematics, 1365). Ed. Giaquinta, M.. Springer, Berlin, 1989, pp. 62–99.Google Scholar
Moser, J.. Quasi-periodic solutions of nonlinear elliptic partial differential equations. Bol. Soc. Brasil. Mat. (N.S.) 20(1) (1989), 29–45.CrossRefGoogle Scholar
Mramor, B.. Monotone variational recurrence relations. PhD Thesis, VU University Amsterdam, 2012.Google Scholar
Mramor, B. and Rink, B. W.. Ghost circles in lattice Aubry–Mather theory. J. Differential Equations 252(4) (2012), 3163–3208.CrossRefGoogle Scholar
Mramor, B. and Rink, B. W.. A dichotomy theorem for minimizers of monotone recurrence relations. Ergod. Th. & Dynam. Sys., to appear, doi:10.1017/etds.2013.47.CrossRefGoogle Scholar
Mramor, B. and Rink, B. W.. On the destruction of minimal foliations. Proc. London Math. Soc. (2013), doi:10.1112/plms/pdt045.CrossRefGoogle Scholar
Salamon, D. and Zehnder, E.. KAM theory in configuration space. Comment. Math. Helv. 64(1) (1989), 84–132.CrossRefGoogle Scholar