Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Parry, William
1997.
Cohomology of permutative cellular automata.
Israel Journal of Mathematics,
Vol. 99,
Issue. 1,
p.
315.
Jenkinson, Oliver
2001.
Strong cocycle triviality for subshifts.
Theoretical Computer Science,
Vol. 262,
Issue. 1-2,
p.
191.


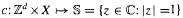 for an expansive and mixing ℤ
for an expansive and mixing ℤ