Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T16:24:37.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Cocycle and orbit equivalence superrigidity for coinduced actions

Published online by Cambridge University Press:  03 April 2017

DANIEL DRIMBE
DANIEL DRIMBE*
Affiliation:
Mathematics Department, University of California, San Diego, CA 90095-1555, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a cocycle superrigidity theorem for a large class of coinduced actions. In particular, if 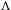$\unicode[STIX]{x1D6EC}$ is a subgroup of a countable group $\unicode[STIX]{x1D6E4}$, we consider a probability measure preserving action 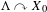$\unicode[STIX]{x1D6EC}\curvearrowright X_{0}$ and let 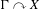$\unicode[STIX]{x1D6E4}\curvearrowright X$ be the coinduced action. Assume either that $\unicode[STIX]{x1D6E4}$ has property (T) or that 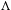$\unicode[STIX]{x1D6EC}$ is amenable and $\unicode[STIX]{x1D6E4}$ is a product of non-amenable groups. Using Popa’s deformation/rigidity theory we prove 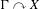$\unicode[STIX]{x1D6E4}\curvearrowright X$ is 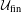${\mathcal{U}}_{\text{fin}}$-cocycle superrigid, that is any cocycle for this action to a 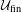${\mathcal{U}}_{\text{fin}}$ (e.g. countable) group 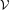${\mathcal{V}}$ is cohomologous to a homomorphism from $\unicode[STIX]{x1D6E4}$ to 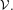${\mathcal{V}}.$

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2644 - 2665
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bowen, L.. Orbit equivalence, coinduced actions and free products. Groups Geom. Dyn. 5(1) (2011), 1–15.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T) (New Mathematical Monographs, 11) . Cambridge University Press, Cambridge, UK, 2008.Google Scholar
Boutonnet, R.. W∗ -superrigidity of mixing Gaussian actions of rigid groups. Adv. Math. 244 (2013), 69–90; http://dx.doi.org/10.1016/j.aim.2013.05.012.Google Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.Google Scholar
Chifan, I., Ioana, A. and Kida, Y.. W∗ -superrigidity for arbitrary actions of central quotients of braid groups. Math. Ann. 361 (2015), 925–959.Google Scholar
Chifan, I. and Kida, Y.. OE and W* superrigidity results for actions by surface braid groups. Proc. Lond. Math. Soc. (3) 111(6) (2015), 1431–1470.Google Scholar
Chifan, I. and Peterson, J.. Some unique group-measure space decomposition results. Duke Math. J. 162(11) (2013), 1923–1966.Google Scholar
Chifan, I. and Sinclair, T.. On the structural theory of II1 factors of negatively curved groups. Ann. Sci. Éc. Norm. Supér. (4) 46 (2013), 1–33.Google Scholar
Chifan, I., Sinclair, T. and Udrea, B.. On the structural theory of II1 factors of negatively curved groups, II. Actions by product groups. Adv. Math. 245 (2013), 208–236.Google Scholar
Dye, H.. On groups of measure preserving transformation. I. Amer. J. Math. 81 (1959), 119–159.Google Scholar
Furman, A.. On Popa’s cocycle superrigidity theorem. Int. Math. Res. Not. IMRN 2007 (2007), 1–46.Google Scholar
Furman, A.. A survey of measured group theory. Geometry, Rigidity, and Group Actions (Chicago Lecture Notes in Mathematics Series) . Eds. Farb, B. and Fisher, D.. The University of Chicago Press, Chicago, IL, 2011, pp. 296–374.Google Scholar
Furman, A.. Orbit equivalence rigidity. Ann. of Math. (2) 150 (1999), 1083–1108.Google Scholar
Furman, A.. Gromov’s measure equivalence and rigidity of higher rank lattices. Ann. of Math. (2) 150 (1999), 1059–1081.Google Scholar
Fima, P. and Vaes, S.. HNN extensions and unique group measure space decomposition of II1 factors. Trans. Amer. Math. Soc. 354 (2012), 2601–2617.Google Scholar
Gaboriau, D.. Orbit equivalence and measured group theory. Proc. Int. Congr. Mathematicians (ICM) (Hyderabad, India, 2010). Vol. III. Hindustan Book Agency, 2010, pp. 1501–1527.Google Scholar
Houdayer, C., Popa, S. and Vaes, S.. A class of groups for which every action is W∗ -superrigid. Groups Geom. Dyn. 7(3) (2013), 577–590.Google Scholar
Ioana, A.. Rigidity results for wreath product of II1 factors. J. Funct. Anal. 252 (2007), 763–791.Google Scholar
Ioana, A.. Orbit inequivalent actions for groups containing a copy of F 2 . Invent. Math. 185 (2011), 55–73.Google Scholar
Ioana, A.. Cocycle superrigidity for profinite actions of property (T) groups. Duke Math J. 157 (2011), 337–367.Google Scholar
Ioana, A.. W∗ -superrigidity for Bernoulli actions of property (T) groups. J. Amer. Math. Soc. 24 (2011), 1175–1226.Google Scholar
Ioana, A.. Classification and rigidity for von Neumann algebras. Proc. 6th Eur. Congr. Mathematics (EMS) (Kraków, Poland, 2–7 July 2012). European Mathematical Society, Zürich, Switzerland, 2014, pp. 601–625.Google Scholar
Ioana, A.. Cartan subalgebras of amalgamated free product of II1 factors. Ann. Sci. Éc. Norm. Supér 48(fascicule 1) (2015), 71–130.Google Scholar
Ioana, A.. Strong ergodicity, property (T), and orbit equivalence rigidity for translation actions. J. Reine. Angew. Math. http://dx.doi.org/10.1515/crelle-2014-0155, published online 28 May 2015.Google Scholar
Ioana, A., Popa, S. and Vaes, S.. A Class of superrigid group von Neumann algebras. Ann. of Math. (2) 178 (2013), 231–286.Google Scholar
Kazhdan, D.. On the connection of the dual space of a group with the structure of its closed subgroups. Funct. Anal. Appl. 1 (1967), 63–65.Google Scholar
Kida, Y.. Measure equivalence rigidity of the mapping class group. Ann. of Math. (2) 171 (2010), 1851–1901.Google Scholar
Kida, Y.. Rigidity of amalgamated free products in measure equivalence. J. Topol. 4 (2011), 687–735.Google Scholar
Margulis, G.. Finitely-additive invariant measures on Euclidean spaces. Ergod. Th. & Dynam. Sys. 2 (1982), 383–396.Google Scholar
Monod, N. and Shalom, Y.. Orbit equivalence rigidity and bounded cohomology. Ann. of Math. (2) 164 (2006), 825–878.Google Scholar
Murray, F. J. and von Neumann, J.. On rings of operators. Ann. of Math. (2) 37 (1936), 116–229.Google Scholar
Ozawa, N. and Popa, S.. On a class of II1 factors with at most one Cartan subalgebra, II. Amer. J. Math. 132 (2010), 841–866.Google Scholar
Ornstein, D. and Weiss, B.. Ergodic theory of amenable group actions. I. The Rohlin lemma. Bull. Amer. Math. Soc. (N.S.) 2(1) (1980), 161–164.Google Scholar
Peterson, J.. Examples of group actions which are virtually W $^{\ast }$ -superrigid. Preprint, 2010, arXiv:1002.1745.Google Scholar
Popa, S.. Strong rigidity of II1 factors arising from malleable actions of w-rigid groups, I. Invent. Math. 165 (2006), 369–408.Google Scholar
Popa, S.. Cocycle and orbit equivalence superrigidity for malleable actions of w-rigid groups. Invent. Math. 170 (2007), 243–295.Google Scholar
Popa, S.. On the superrigidity of malleable actions with spectral gap. J. Amer. Math. Soc. 21 (2008), 981–1000.Google Scholar
Popa, S.. Deformation and rigidity for group actions and von Neumann algebras. Proc. Int. Congr. Mathematicians (ICM) (Madrid, 22–30 August 2006). Vol. I. European Mathematical Society, Zürich, Switzerland, 2007, pp. 445–477.Google Scholar
Peterson, J. and Sinclair, T.. On cocycle superrigidity for Gaussian actions. Ergod. Th. & Dynam. Sys. 32(1) (2012), 249–272.Google Scholar
Popa, S. and Vaes, S.. Strong rigidity of generalized Bernoulli actions and computations of their symmetry groups. Adv. Math. 217 (2008), 833–872.Google Scholar
Popa, S. and Vaes, S.. Cocycle and Orbit Superrigidity for Lattices in SL(n, ℝ) Acting on Homogeneous Spaces (Geometry, Rigidity and Group Actions, 182) . Eds. Farb, B. and Fisher, D.. The University of Chicago Press, Chicago, IL, 2011, pp. 419–541.Google Scholar
Popa, S. and Vaes, S.. Group measure space decomposition of II1 factors and W-superrigidity. Invent. Math. 182(2) (2010), 371–417.Google Scholar
Popa, S. and Vaes, S.. Unique Cartan decomposition for II1 factors arising from arbitrary actions of free groups. Acta Math. 212 (2014), 141–198.Google Scholar
Popa, S. and Vaes, S.. Unique Cartan decomposition for II1 factors arising from arbitrary actions of hyperbolic groups. J. Reine Angew. Math. 690 (2014), 433–458.Google Scholar
Singer, I. M.. Automorphism of finite factors. Amer. J. Math. 77 (1955), 117–133.Google Scholar
Tucker-Drob, R. D.. Invariant means and the structure of inner amenable groups. Preprint, 2014,arXiv:1407.7474.Google Scholar
Vaes, S.. Rigidity results for Bernoulli actions and their von Neumann algebras (after Sorin Popa), Séminaire Bourbaki, expos 961. Astérisque 311 (2007), 237–294.Google Scholar
Vaes, S.. Rigidity for von Neumann algebras and their invariants. Proc. Int. Congr. Mathematicians (ICM) (Hyderabad, India, 2010), Vol. III. Hindustan Book Agency, 2010, pp. 1624–1650.Google Scholar
Vaes, S.. One-cohomology and the uniqueness of the group measure space decomposition of a II1 factor. Math. Ann. 355 (2013), 661–696.Google Scholar
Zimmer, R.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81) . Birkḧauser, Basel, 1984.Google Scholar