Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T16:46:24.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Coalescence of circle extensions of measure-preserving transformations

Published online by Cambridge University Press:  19 September 2008

Mariusz Lemańczyk ,
Pierre Liardet  and
Jean-Paul Thouvenot
Mariusz Lemańczyk
Affiliation:
Institute of Mathematics, Nicholas Copernicus University, ul. Chopina 12/18, 87–100, Poland
Pierre Liardet
Affiliation:
Université de Provence, U.R. Associée aux CNRS no 225, 3, place V. Hugo, F-13331 Marseille Cedex 3, France
Jean-Paul Thouvenot
Affiliation:
Laboratoire de Probabilités, Université ParisVI, 75252 Paris Cedex 05, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for each ergodic automorphism T:(X, ℬ, μ)→(X, ℬ, μ) for which we can find an element S∈C(T) such that the corresponding Z2-action (S, T) on (X, ℬ, μ) is free, there exists a circle valued cocycle φ such that the group extension Tφ is ergodic but is not coalescent. In particular, the existence of such a cocycle is proved for all ergodic rigid automorphisms. As a corollary, in the class of ergodic transformations of [0,1) × [0,1) given by

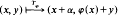
for each irrational α we find φ such that Tφ is not coalescent. In some special cases the group law of the centralizer is given.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 4 , December 1992 , pp. 769 - 789
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anzai, H.. Ergodic skew-product transformations on the torus. Osaka J. Math. 3 (1951), 83–99.Google Scholar
[2]Conze, J.-P.. Entropie d'un groupe abélien de transformations. Z. Wahr. Verw. Geb. 25 (1972), 11–30.CrossRefGoogle Scholar
[3]Furstenberg, H.. Strict ergodicity and transformations of the torus. Amer. J. Math. 89 (1961), 573–601.CrossRefGoogle Scholar
[4]Furstenberg, H.. Disjointness in ergodic theory, minimal sets and diophantine approximation. Math. Syst. Th. 1 (1967), 1–49.CrossRefGoogle Scholar
[5]Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, New Jersey, 1981.CrossRefGoogle Scholar
[6]Gabriel, P., Lemańczyk, M. & Liardet, P.. Ensemble d'invariants pour les produits croisés de Anzai. Mémoire Soc. Math. France 119 (1991), 1–102.Google Scholar
[7]Hahn, F. & Parry, W.. Some characteristic properties of dynamical systems with quasi-discrete spectrum. Math. Sys. Th. 2 (1968), 179–190.CrossRefGoogle Scholar
[8]Halmos, P. R.. Lectures on Ergodic Theory. Chelsea Publ. Company, New York, 1956.Google Scholar
[9]Herman, M.. Sur la conjugaison différentiate des difféomorphismes du cercle à des rotations. Thèse de Doctorat d'Etat. Université Paris-Sud, 1976.Google Scholar
[10]del Junco, A. & Rudolph, D.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7 (1987), 531–558.CrossRefGoogle Scholar
[11]Katznelson, Y. & Weiss, B.. Commuting measure-preserving transformations. Israel J. Math. 12 (1972), 161–173.CrossRefGoogle Scholar
[12]Kwiatkowski, J. & Lemańczyk, M.. The centralizer of ergodic theory group extensions. Banach Center Publ. vol. 24, Warszawa, 1989, pp. 455–463.Google Scholar
[13]Kwiatkowski, J., Lemańczyk, M. & Rudolph, D.. The weak isomorphisms of measure-preserving diffeomorphisms. Submitted.Google Scholar
[14]Kwiatkowski, J., Lemańczyk, M. & Rudolph, D.. A class of real cocycles having an analytic coboundary modification. Preprint.CrossRefGoogle Scholar
[15]Lemańczyk, M.. Weakly isomorphic transformations that are not isomorphic. Prob. Th. Rel. Fields 78 (1988), 491–507.CrossRefGoogle Scholar
[16]Liardet, P.. Propriétés génériques de processus croisés. Isr. J. Math. 39 (1981), 303–325.CrossRefGoogle Scholar
[17]Liardet, P.. Regularities of distribution. Compositio Math. 61 (1987), 267–293.Google Scholar
[18]Newton, D.. Coalescence and spectrum of automorphisms of a Lebesgue space. Z. Wahr. verw. Geb. 19(1971), 117–122.CrossRefGoogle Scholar
[19]Newton, D.. On canonical factors of ergodic dynamical systems. J. London Math. Soc. 19 (1979), 129–136.CrossRefGoogle Scholar
[20]Parry, W.. Compact abelian group extensions of discrete dynamical systems. Z. Wahr. verw. Geb. 17(1969), 95–113.CrossRefGoogle Scholar
[21]Parry, W. & Walters, P.. Minimal skew product homeomorphisms and coalescence. Composito Math. 32 (1970), 283–288.Google Scholar
[22]Thouvenot, J.-P.. Quelques propriét´es des systèmes dynamiques qui se décomposent en un produit de deux systèmes dont l'un est un schéma de Bernoulli. Isr. J. Math. 21 (1975), 177–207.CrossRefGoogle Scholar
[23]Varadarajan, V. S.. Geometry of Quantum Theory, vol. II. Van Nostrand Reinhold, New York, 1970.Google Scholar