Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T12:31:35.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Center foliation: absolute continuity, disintegration and rigidity

Published online by Cambridge University Press:  11 August 2014

RÉGIS VARÃO
RÉGIS VARÃO*
Affiliation:
Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Avenida Trabalhador São-Carlense, 400, 13566-590, São Carlos, SP, Brasil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we address the issues of absolute continuity for the center foliation, as well as the disintegration on the non-absolute continuous case and rigidity of volume-preserving partially hyperbolic diffeomorphisms isotopic to a linear Anosov automorphism on 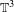$\mathbb{T}^{3}$. It is shown that the disintegration of volume on center leaves for these diffeomorphisms may be neither atomic nor Lebesgue, in contrast to the dichotomy (Lebesgue or atomic) obtained by Avila, Viana and Wilkinson [Absolute continuity, Lyapunov exponents and rigidity I: Geodesic flows. Preprint, 2012, arXiv:1110.2365v2] for perturbations of time-one of geodesic flow. In the case of atomic disintegration of volume on the center leaves of an Anosov diffeomorphism on 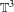$\mathbb{T}^{3}$, we show that it has to be one atom per leaf. Moreover, we show that not even a 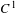$C^{1}$ center foliation implies a rigidity result. However, for a volume-preserving partially hyperbolic diffeomorphism isotopic to a linear Anosov automorphism, assuming the center foliation is 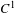$C^{1}$ and transversely absolutely continuous with bounded Jacobians, we obtain smooth conjugacy to its linearization.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 256 - 275
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Viana, M. and Wilkinson, A.. Absolute continuity, Lyapunov exponents and rigidity I: Geodesic flows. Preprint, 2012, arXiv:1110.2365v2.Google Scholar
Baraviera, A. T. and Bonatti, C.. Removing zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 23(6) (2003), 1655–1670.CrossRefGoogle Scholar
Bonatti, C., Diaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102; Mathematical Physics, III). Springer, Berlin, 2005.Google Scholar
Bonatti, C. and Wilkinson, A.. Transitive partially hyperbolic diffeomorphisms on 3-manifolds. Topology 44(3) (2005), 475–508.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and The Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 2008.CrossRefGoogle Scholar
Brin, M., Burago, D. and Ivanov, S.. Dynamical coherence of partially hyperbolic diffeomorphisms of the 3-torus. J. Mod. Dyn. 3(1) (2009), 1–11.CrossRefGoogle Scholar
Gogolev, A.. How typical are pathological foliations in partially hyperbolic dynamics: an example. Israel J. Math. 187 (2012), 493–507.CrossRefGoogle Scholar
Gogolev, A. and Guysinsky, M.. C 1 -differentiable conjugacy of Anosov diffeomorphisms on three dimensional torus. Discrete Contin. Dyn. Syst. 22(1–2) (2008), 183–200.Google Scholar
Hammerlindl, A.. Leaf conjugacies on the torus. Ergod. Th. & Dynam. Sys. 33(3) (2013), 896–933.CrossRefGoogle Scholar
Hasselblatt, B.. Hyperbolic Dynamical Systems (Handbook of dynamical systems, vol. 1A). North-Holland, Amsterdam, 2002, pp. 239–319.Google Scholar
Homburg, A.. Atomic disintegrations for partially hyperbolic diffeomorphisms. Preprint, 2014. Available from http://staff.science.uva.nl/∼alejan/ajh-research.html.Google Scholar
Ponce, G., Tahzibi, A. and Varão, R.. Minimal yet measurable foliations. J. Mod. Dynam. to appear,doi:10.3934/jmd.2014.8.1.Google Scholar
Ruelle, D. and Wilkinson, A.. Absolutely singular dynamical foliations. Comm. Math. Phys. 219 (2001), 481–487.CrossRefGoogle Scholar
Saghin, R. and Xia, Z.. Geometric expansion, Lyapunov exponents and foliations. Ann. Inst. H. Poincaré Anal. Non Lineaire 26(2) (2009), 689–704.CrossRefGoogle Scholar
Sambarino, M.. Hiperbolicidad y Estabilidad. Ediciones IVIC, Venezuela, 2009.Google Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Proc. Symp. Pure Math., Vol. XIV, Berkeley, CA, 1968). American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar