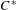Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T14:37:42.678Z Has data issue: false hasContentIssue false
  • English
  • Français

$C^{\ast }$-algebras of labelled graphs III—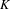$K$-theory computations

Published online by Cambridge University Press:  06 October 2015

TERESA BATES ,
TOKE MEIER CARLSEN  and
DAVID PASK
TERESA BATES
Affiliation:
School of Mathematics and Statistics, University of New South Wales, UNSW Sydney, NSW 2052, Australia email [email protected]
TOKE MEIER CARLSEN
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology (NTNU), 7491 Trondheim, Norway email [email protected]
DAVID PASK
Affiliation:
School of Mathematics and Applied Statistics, Austin Keane Building (15), University of Wollongong, NSW 2522, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give a formula for the 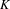$K$-theory of the 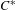$C^{\ast }$-algebra of a weakly left-resolving labelled space. This is done by realizing the 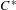$C^{\ast }$-algebra of a weakly left-resolving labelled space as the Cuntz–Pimsner algebra of a 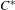$C^{\ast }$-correspondence. As a corollary, we obtain a gauge-invariant uniqueness theorem for the 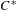$C^{\ast }$-algebra of any weakly left-resolving labelled space. In order to achieve this, we must modify the definition of the 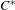$C^{\ast }$-algebra of a weakly left-resolving labelled space. We also establish strong connections between the various classes of 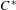$C^{\ast }$-algebras that are associated with shift spaces and labelled graph algebras. Hence, by computing the 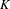$K$-theory of a labelled graph algebra, we are providing a common framework for computing the 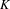$K$-theory of graph algebras, ultragraph algebras, Exel–Laca algebras, Matsumoto algebras and the 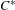$C^{\ast }$-algebras of Carlsen. We provide an inductive limit approach for computing the 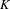$K$-groups of an important class of labelled graph algebras, and give examples.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 2 , April 2017 , pp. 337 - 368
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Huef, A. an and Raeburn, I.. The ideal structure of Cuntz–Krieger algebras. Ergod. Th. & Dynam. Sys. 17 (1997), 611–624.Google Scholar
Bates, T., Eilers, S. and Pask, D.. Reducibility of covers of AFT shifts. Israel J. Math. 185 (2011), 207–234.Google Scholar
Bates, T. and Pask, D.. C ∗ -algebras of labelled graphs. J. Operator Theory 57 (2007), 207–226.Google Scholar
Bates, T. and Pask, D.. C ∗ -algebras of labelled graphs II—simplicity results. Math. Scand. 104 (2009), 249–274.Google Scholar
Bates, T., Pask, D. and Willis, P.. Group actions on labeled graphs and their C ∗ -algebras. Illinois J. Math. 56 (2012), 1149–1168.Google Scholar
Bowen, R. and Franks, J.. Homology for zero-dimensional nonwandering sets. Ann. Math. 106 (1977), 73–92.Google Scholar
Carlsen, T. M.. Symbolic dynamics, partial dynamical systems, boolean algebras and $C^{\ast }$ -algebras generated by partial isometries. Preprint, 2006, arXiv:0604165, 55 pp.Google Scholar
Carlsen, T. M.. Cuntz–Pimsner C ∗ -algebras associated with subshifts. Internat. J. Math. 19 (2008), 47–70.Google Scholar
Carlsen, T. M. and Eilers, S.. Augmenting dimension group invariants for substitution dynamics. Ergod. Th. & Dynam. Sys. 24 (2004), 1015–1039.Google Scholar
Carlsen, T. M. and Eilers, S.. Ordered K-groups associated to substitutional dynamics. J. Funct. Anal. 238 (2006), 99–117.Google Scholar
Carlsen, T. M. and Matsumoto, K.. Some remarks on the C ∗ -algebras associated with subshifts. Math. Scand. 95 (2004), 145–160.Google Scholar
Carlsen, T. M. and Silvestrov, S.. C*-crossed products and shift spaces. Expo. Math. 25 (2007), 275–307.CrossRefGoogle Scholar
Carlsen, T. M. and Silvestrov, S.. On the K-theory of the C ∗ -algebra associated to a one-sided shift space. Proc. Est. Acad. Sci. 59 (2010), 272–279.Google Scholar
Cuntz, J.. A class of C ∗ -algebras and topological Markov chains: reducible chains and the Ext-functor for C ∗ -algebras. Invent. Math. 63 (1981), 25–40.Google Scholar
Cuntz, J. and Krieger, W.. A class of C ∗ -algebras and topological Markov chains. Invent. Math. 56 (1980), 251–268.Google Scholar
Drinen, D. and Tomforde, M.. Computing K-theory and Ext for graph C ∗ -algebras. Illinois J. Math. 46 (2002), 81–91.Google Scholar
Enomoto, M. and Watatani, Y.. A graph theory for C ∗ -algebras. Math. Japon. 25 (1980), 435–442.Google Scholar
Exel, R. and Laca, M.. Cuntz–Krieger algebras for infinite matrices. J. Reine Angew. Math. 512 (1999), 119–172.CrossRefGoogle Scholar
Fowler, N., Laca, M. and Raeburn, I.. The C ∗ -algebras of infinite graphs. Proc. Amer. Math. Soc. 128 (2000), 2319–2327.CrossRefGoogle Scholar
Fowler, N. and Raeburn, I.. The Toeplitz algebra of a Hilbert bimodule. Indiana Univ. Math. J. 48 (1999), 155–181.Google Scholar
Giordano, T., Putnam, I. and Skau, C.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Jeong, J. and Kim, S.. On simple labelled graph C ∗ -algebras. J. Math. Anal. Appl. 386 (2012), 631–640.Google Scholar
Katsura, T.. On C ∗ -algebras associated with C ∗ -correspondences. J. Funct. Anal. 217 (2004), 366–401.Google Scholar
Katsura, T.. Nonseparable AF algebras. Operator Algebras: The Abel Symposium 2004 (Abel Symposia, 1) . Springer, Berlin, 2006, pp. 165–173.Google Scholar
Katsura, T., Muhly, P. S., Sims, A. and Tomforde, M.. Ultragraph C ∗ -algebras via topological quivers. Studia Math. 187 (2008), 137–155.Google Scholar
Katsura, T., Muhly, P. S., Sims, A. and Tomforde, M.. Graph algebras, Exel–Laca algebras, and ultragraph algebras coincide up to Morita equivalence. J. Reine Angew. Math. 640 (2010), 135–165.Google Scholar
Krieger, W.. On sofic systems I. Israel J. Math. 48 (1984), 305–330.Google Scholar
Krieger, W. and Matsumoto, K.. Shannon graphs, subshifts and lambda-graph systems. J. Math. Soc. Japan 54 (2002), 877–899.CrossRefGoogle Scholar
Krieger, W. and Matsumoto, K.. A lambda-graph system for the Dyck shift and its K-groups. Doc. Math. 8 (2003), 79–96.Google Scholar
Kumjian, A., Pask, D. and Raeburn, I.. Cuntz–Krieger algebras of directed graphs. Pacific J. Math. 184 (1998), 161–174.Google Scholar
Matsumoto, K.. On C ∗ -algebras associated with subshifts. Internat. J. Math. 8 (1997), 357–374.Google Scholar
Matsumoto, K.. K-theory for C ∗ -algebras associated with subshifts. Math. Scand. 82 (1998), 237–255.CrossRefGoogle Scholar
Matsumoto, K.. Dimension groups for subshifts and simplicity of the associated C ∗ -algebras. J. Math. Soc. Japan 51 (1999), 679–698.Google Scholar
Matsumoto, K.. Relations among generators of C ∗ -algebras associated with subshifts. Internat. J. Math. 10 (1999), 385–405.CrossRefGoogle Scholar
Matsumoto, K.. Presentations of subshifts and their topological conjugacy invariants. Doc. Math. 4 (1999), 285–340.Google Scholar
Matsumoto, K.. On automorphisms of C ∗ -algebras associated with subshifts. J. Operator Theory 44 (2000), 91–112.Google Scholar
Matsumoto, K.. Stabilized C ∗ -algebras constructed from symbolic dynamical systems. Ergod. Th. & Dynam. Sys. 20 (2000), 821–841.Google Scholar
Matsumoto, K.. Bowen–Franks groups as an invariant for flow equivalence of subshifts. Ergod. Th. & Dynam. Sys. 21 (2001), 1831–1842.Google Scholar
Matsumoto, K.. Bowen–Franks groups for subshifts and Ext-groups for C ∗ -algebras. K-Theory 23 (2001), 67–104.Google Scholar
Matsumoto, K.. C ∗ -algebras associated with presentations of subshifts. Doc. Math. 7 (2002), 1–30.Google Scholar
Pimsner, M. V.. A class of C ∗ -algebras generalizing both Cuntz–Krieger algebras and crossed products by Z . Free Probability Theory (Waterloo, ON, 1995 (Fields Institute Communications, 12) . American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
Robertson, D. and Szymański, W.. C ∗ -algebras associated to C ∗ -correspondences and applications to mirror quantum spheres. Illinois J. Math. 55 (2011), 845–870.Google Scholar
Tomforde, M.. A unified approach to Exel–Laca algebras and C ∗ -algebras associated to graphs. J. Operator Theory 50 (2003), 345–368.Google Scholar
Tomforde, M.. Simplicity of ultragraph algebras. Indiana Univ. Math. J. 52 (2003), 901–926.Google Scholar
Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor. Duke Math. J. 55 (1987), 431–474.Google Scholar
Szymański, W.. The range of K-invariants for C ∗ -algebras of infinite graphs. Indiana Univ. Math. J. 51 (2002), 239–249.Google Scholar