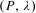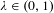Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gaivão, José Pedro
and
Nogueira, Arnaldo
2022.
Dynamics of piecewise increasing contractions.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 2,
p.
482.
Gaivão, José Pedro
Laurent, Michel
and
Nogueira, Arnaldo
2024.
Rotation number of 2-interval piecewise affine maps.
Aequationes mathematicae,
JAIN, SAKSHI
and
LIVERANI, CARLANGELO
2025.
Piecewise contractions.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 5,
p.
1503.