Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-13T08:47:12.558Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximating the maximum ergodic average via periodic orbits

Published online by Cambridge University Press:  01 August 2008

D. COLLIER  and
I. D. MORRIS
D. COLLIER
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK (email: [email protected])
I. D. MORRIS
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let σ:ΣA→ΣA be a subshift of finite type, let 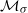be the set of all σ-invariant Borel probability measures on ΣA, and let 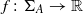be a Hölder continuous observable. There exists at least one σ-invariant measure μ which maximizes 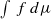. The following question was asked by B. R. Hunt, E. Ott and G. Yuan: how quickly can the maximum of the integrals 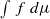be approximated by averages along periodic orbits of period less than p? We give an example of a Hölder observable f for which this rate of approximation is slower than stretched-exponential in p.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 4 , August 2008 , pp. 1081 - 1090
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16 (2003), 419–426.CrossRefGoogle Scholar
[2]Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. H. Poincaré Probab. Statist. 36 (2000), 489–508.CrossRefGoogle Scholar
[3]Bousch, T. and Jenkinson, O.. Cohomology classes of dynamically non-negative C k functions. Invent. Math. 148 (2002), 207–217.CrossRefGoogle Scholar
[4]Bousch, T. and Mairesse, J.. Asymptotic height optimization for topical IFS, tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc. 15 (2002), 77–111.CrossRefGoogle Scholar
[5]Bressaud, X. and Quas, A.. Rates of approximation of minimizing measures. Nonlinearity 20 (2007), 845–853.CrossRefGoogle Scholar
[6]Contreras, G., Lopes, A. and Thieullen, P.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 5 (2001), 1379–1409.Google Scholar
[7]Hunt, B. and Ott, E.. Optimal periodic orbits of chaotic systems occur at low period. Phys. Rev. E 54 (1996), 328–337.Google Scholar
[8]Jenkinson, O.. Ergodic optimization. Disc. Cont. Dyn. Syst. 15 (2006), 197–224.CrossRefGoogle Scholar
[9]Jenkinson, O.. Rotation, entropy and equilibrium states. Trans. Amer. Math. Soc. 353 (2001), 3713–3739.CrossRefGoogle Scholar
[10]Parthasarathy, K. R.. On the category of ergodic measures. Illinois J. Math. 5 (1961), 648–656.Google Scholar
[11]Yuan, G. and Hunt, B.. Optimal orbits of hyperbolic systems. Nonlinearity 12(4) (1999), 1207–1224.Google Scholar