No CrossRef data available.
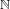 $\mathbb{N}$ on
$\mathbb{N}$ on  $\{0,1\}^{\mathbb{N}}$
$\{0,1\}^{\mathbb{N}}$Published online by Cambridge University Press: 13 March 2018
In this paper we show that the natural action of the symmetric group acting on the product space 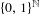 $\{0,1\}^{\mathbb{N}}$ endowed with a Bernoulli measure is approximately transitive. We also extend the result to a larger class of probability measures.
$\{0,1\}^{\mathbb{N}}$ endowed with a Bernoulli measure is approximately transitive. We also extend the result to a larger class of probability measures.