Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-08T18:30:13.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Any Baumslag–Solitar action on surfaces with a pseudo-Anosov element has a finite orbit

Published online by Cambridge University Press:  28 March 2018

NANCY GUELMAN  and
ISABELLE LIOUSSE
NANCY GUELMAN
Affiliation:
IMERL, Facultad de Ingeniería, Universidad de la República, C.C. 30, Montevideo, Uruguay email [email protected]
ISABELLE LIOUSSE
Affiliation:
Laboratoire Paul Painlevé, Université de Lille 1, 59655 Villeneuve d’Ascq Cédex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider homeomorphisms $f,h$ generating a faithful 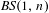$\mathit{BS}(1,n)$-action on a closed surface $S$, that is, 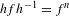$hfh^{-1}=f^{n}$ for some $n\geq 2$. According to Guelman and Liousse [Actions of Baumslag–Solitar groups on surfaces. Discrete Contin. Dyn. Syst. A 5 (2013), 1945–1964], after replacing 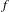$f$ by a suitable iterate if necessary, we can assume that there exists a minimal set 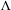$\unicode[STIX]{x1D6EC}$ of the action, included in 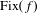$\text{Fix}(f)$. Here, we suppose that 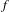$f$ and 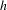$h$ are 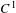$C^{1}$ in a neighborhood of 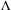$\unicode[STIX]{x1D6EC}$ and any point 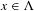$x\in \unicode[STIX]{x1D6EC}$ admits an 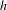$h$-unstable manifold 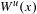$W^{u}(x)$. Using Bonatti’s techniques, we prove that either there exists an integer 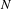$N$ such that 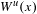$W^{u}(x)$ is included in 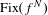$\text{Fix}(f^{N})$ or there is a lower bound for the norm of the differential of 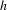$h$ depending only on $n$ and the Riemannian metric on $S$. Combining the last statement with a result of Alonso, Guelman and Xavier [Actions of solvable Baumslag–Solitar groups on surfaces with (pseudo)-Anosov elements. Discrete Contin. Dyn. Syst. to appear], we show that any faithful action of 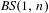$\mathit{BS}(1,n)$ on $S$ with 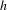$h$ a pseudo-Anosov homeomorphism has a finite orbit containing singularities of 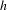$h$; moreover, if 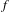$f$ is isotopic to the identity, it is entirely contained in the singular set of 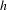$h$. 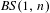As a consequence, there is no faithful $C^{1}$-action of $\mathit{BS}(1,n)$ on the torus with 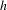$h$ Anosov.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3353 - 3364
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alonso, J., Guelman, N. and Xavier, J.. Actions of solvable Baumslag–Solitar groups on surfaces with (pseudo)-Anosov elements. Discrete Contin. Dyn. Syst. 35(5) (2015), 1817–1827.Google Scholar
Bonatti, C., Monteverde, I., Navas, A. and Rivas, C.. Rigidity for C1 actions on the interval arising from hyperbolicity I: solvable groups. Math. Z. 286(3–4) (2017), 919–949.Google Scholar
Bonatti, C.. Un point fixe commun pour des difféomorphismes commutants de S 2 . Ann. of Math. (2) 129(2) (1989), 61–69.Google Scholar
Burslem, L. and Wilkinson, A.. Global rigidity of solvable group actions on S 1 . Geom. Topol. 8 (2004), 877–924.Google Scholar
Druck, S., Fang, F. and Firmo, S.. Fixed points of discrete nilpotent group actions on S 2 . Ann. Inst. Fourier (Grenoble) 52(4) (2002), 1075–1091.Google Scholar
Franks, J., Handel, M. and Parwani, K.. Fixed points of abelian actions. J. Mod. Dyn. 1(3) (2007), 443–464.Google Scholar
Farb, B., Lubotzky, A. and Minsky, Y.. Rank-1 phenomena for mapping class groups. Duke Math. J. 106(3) (2001), 581–597.Google Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton Mathematical Series, 49) . Princeton University Press, Princeton, NJ, 2012.Google Scholar
Firmo, S. and Ribón, J.. Finite orbits for nilpotent actions on the torus. Proc. Amer. Math. Soc. 146(1) (2018), 195–208.Google Scholar
Guelman, N. and Liousse, I.. Actions of Baumslag–Solitar groups on surfaces. Discrete Contin. Dyn. Syst. A 5 (2013), 1945–1964.Google Scholar
Guelman, N. and Liousse, I.. C 1 actions of Baumslag Solitar groups on S 1 . Algebr. Geom. Topol. 11 (2011), 1701–1707.Google Scholar
Hirsch, M.. Fixed points of local actions of Lie groups on real and complex 2-manifolds. Axioms 4 (2015), 313–320.Google Scholar
Hirsch, M.. Fixed points of local actions of nilpotent Lie groups on surfaces. Ergod. Th. & Dynam. Sys. 4 (2016), 1–15.Google Scholar
Hirsch, M. and Weinstein, A.. Fixed points of analytic actions of supersoluble Lie groups on compact surfaces. Ergod. Th. & Dynam. Sys. 21 (2001), 1783–1787.Google Scholar
Lima, E.. Common singularities of commuting vector fields on 2-manifolds. Comment. Math. Helv. 39 (1964), 97–110.Google Scholar
McCarthy, A.. Rigidity of trivial actions of abelian-by-cyclic groups. Proc. Amer. Math. Soc. 138 (2010), 1395–1403.Google Scholar
Plante, J. F.. Fixed points of Lie group actions on surfaces. Ergod. Th. & Dynam. Sys. 6 (1986), 149–161.Google Scholar
Weaver, N.. Pointwise periodic homeomorphisms of continua. Ann. of Math. (2) 95(1) (1972), 83–85.Google Scholar