Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:09:49.452Z Has data issue: false hasContentIssue false
  • English
  • Français

An Abramov formula for stationary spaces of discrete groups

Published online by Cambridge University Press:  15 January 2013

YAIR HARTMAN ,
YURI LIMA  and
OMER TAMUZ
YAIR HARTMAN
Affiliation:
Weizmann Institute of Science, Faculty of Mathematics and Computer Science, PO Box 26, 76100, Rehovot, Israel email [email protected]@[email protected]
YURI LIMA
Affiliation:
Weizmann Institute of Science, Faculty of Mathematics and Computer Science, PO Box 26, 76100, Rehovot, Israel email [email protected]@[email protected]
OMER TAMUZ
Affiliation:
Weizmann Institute of Science, Faculty of Mathematics and Computer Science, PO Box 26, 76100, Rehovot, Israel email [email protected]@[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 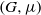$(G, \mu )$ be a discrete group equipped with a generating probability measure, and let 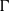$\Gamma $ be a finite index subgroup of 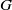$G$. A 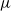$\mu $-random walk on 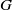$G$, starting from the identity, returns to 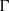$\Gamma $ with probability one. Let 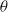$\theta $ be the hitting measure, or the distribution of the position in which the random walk first hits 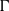$\Gamma $. We prove that the Furstenberg entropy of a 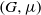$(G, \mu )$-stationary space, with respect to the action of 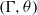$(\Gamma , \theta )$, is equal to the Furstenberg entropy with respect to the action of 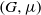$(G, \mu )$, times the index of 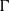$\Gamma $ in 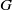$G$. The index is shown to be equal to the expected return time to 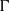$\Gamma $. As a corollary, when applied to the Furstenberg–Poisson boundary of 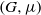$(G, \mu )$, we prove that the random walk entropy of 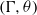$(\Gamma , \theta )$ is equal to the random walk entropy of 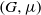$(G, \mu )$, times the index of 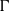$\Gamma $ in 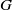$G$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 837 - 853
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramov, L. M.. The entropy of a derived automorphism. Dokl. Akad. Nauk SSSR 128 (1959), 647–650(in Russian).Google Scholar
Avez, A.. Entropie des groupes de type fini. C. R. Acad. Sci. Paris Sér. A-B 275 (1972), 1363–1366(in French).Google Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163 (2) (2006), 415–454.Google Scholar
Furman, A.. Random walks on groups and random transformations. Handbook of Dynamical Systems. Vol. 1A. North-Holland, Amsterdam, 2002, pp. 931–1014.Google Scholar
Furstenberg, H.. Random walks and discrete subgroups of Lie groups. Adv. Probab. Relat. Topics 1 (1971), 1–63.Google Scholar
Furstenberg, H. and Glasner, E.. Stationary dynamical systems. Dynamical Numbers—Interplay Between Dynamical Systems and Number Theory (Contemporary Mathematics, 532). American Mathematical Society, Providence, RI, 2010, pp. 1–28.Google Scholar
Kaimanovich, V. A. and Vershik, A. M.. Random walks on discrete groups: boundary and entropy. Ann. Probab. 11 (3) (1983), 457–490.Google Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L.. Markov Chains and Mixing Times. American Mathematical Society, Providence, RI, 2009.Google Scholar
Nevo, A. and Zimmer, R. J.. Homogenous projective factors for actions of semi-simple Lie groups. Invent. Math. 138 (2) (1999), 229–252.Google Scholar