Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T09:07:46.849Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost minimal systems and periodicity in hyperspaces

Published online by Cambridge University Press:  14 March 2017

LEOBARDO FERNÁNDEZ ,
CHRIS GOOD  and
MATE PULJIZ Open the ORCID record for MATE PULJIZ [Opens in a new window]
LEOBARDO FERNÁNDEZ
Affiliation:
Facultad de Ciencias, Universidad Nacional Autónoma de México, Circuito Exterior, Ciudad Universitaria, México D.F., C.P. 04510, México email [email protected]
CHRIS GOOD
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK email [email protected], [email protected]
MATE PULJIZ
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a self-map of a compact metric space 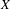$X$, we study periodic points of the map induced on the hyperspace of closed non-empty subsets of 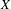$X$. We give some necessary conditions on admissible sets of periods for these maps. Seemingly unrelated to this, we construct an almost totally minimal homeomorphism of the Cantor set. We also apply our theory to give a full description of admissible period sets for induced maps of the interval maps. The description of admissible periods is also given for maps induced on symmetric products.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2158 - 2179
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Glasner, E. and Weiss, B.. Generically there is but one self homeomorphism of the Cantor set. Trans. Amer. Math. Soc. 360(7) (2008), 3613–3630.Google Scholar
Amini, M., Elliott, G. A. and Golestani, N.. The category of Bratteli diagrams. Canad. J. Math. 67(5) (2015), 990–1023.Google Scholar
Balibrea, F., Guirao, J. L. G. and Lampart, M.. A note on the definition of 𝛼-limit set. Appl. Math. Inf. Sci. 7(5) (2013), 1929–1932.Google Scholar
Banks, J.. Chaos for induced hyperspace maps. Chaos Solitons Fractals 25(3) (2005), 681–685.Google Scholar
Bauer, W. and Sigmund, K.. Topological dynamics of transformations induced on the space of probability measures. Monatsh. Math. 79(2) (1975), 81–92.Google Scholar
Bernardes, N. C. Jr. and Darji, U. B.. Graph theoretic structure of maps of the Cantor space. Adv. Math. 231(3–4) (2012), 1655–1680.Google Scholar
Block, L. S. and Coppel, W. A.. Dynamics in One Dimension (Lecture Notes in Mathematics, 1513) . Springer, Berlin, 1992.Google Scholar
Block, L. and Coven, E. M.. Maps of the interval with every point chain recurrent. Proc. Amer. Math. Soc. 98(3) (1986), 513–515.Google Scholar
Danilenko, A. I.. Strong orbit equivalence of locally compact Cantor minimal systems. Internat. J. Math. 12(1) (2001), 113–123.Google Scholar
Dooley, A. H.. Markov odometers. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 60–80.Google Scholar
Edalat, A.. Dynamical systems, measures, and fractals via domain theory. Inform. and Comput. 120(1) (1995), 32–48.Google Scholar
Fernández, L. and Good, C.. Shadowing for induced maps of hyperspaces. Fund. Math. 235(2) (2016), 277–286.Google Scholar
Fernández, L., Good, C., Puljiz, M. and Ramírez, Á.. Chain transitivity in hyperspaces. Chaos Solitons Fractals 81(part A) (2015), 83–90.Google Scholar
Gambaudo, J.-M. and Martens, M.. Algebraic topology for minimal Cantor sets. Ann. Henri Poincaré 7(3) (2006), 423–446.Google Scholar
Gómez-Rueda, J. L., Illanes, Al. and Méndez, H.. Dynamic properties for the induced maps in the symmetric products. Chaos Solitons Fractals 45(9–10) (2012), 1180–1187.Google Scholar
Guirao, J. L. G., Kwietniak, D., Lampart, M., Oprocha, P. and Peris, A.. Chaos on hyperspaces. Nonlinear Anal. 71(1–2) (2009), 1–8.Google Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(6) (1992), 827–864.Google Scholar
Ingram, W. T. and Mahavier, W. S.. Inverse Limits (Developments in Mathematics, 25) . Springer, New York, 2012.Google Scholar
Kwietniak, D. and Oprocha, P.. Topological entropy and chaos for maps induced on hyperspaces. Chaos Solitons Fractals 33(1) (2007), 76–86.Google Scholar
Mioduszewski, J.. Mappings of inverse limits. Colloq. Math. 10(1) (1963), 39–44.Google Scholar
Nadler, S. B. Jr.. Hyperspaces of sets. A text with research questions. Aportaciones Matemáticas: Textos [Mathematical Contributions: Texts]. 33 Sociedad Matemática Mexicana, Mexico City, México, 2006.Google Scholar
Nagami, K.. Dimension Theory (Pure and Applied Mathematics, 37) . Academic Press, New York, 1970, with an appendix by Yukihiro Kodama.Google Scholar
Shimomura, T.. Special homeomorphisms and approximation for Cantor systems. Topology Appl. 161 (2014), 178–195.Google Scholar
Shimomura, T.. The construction of a completely scrambled system by graph covers. Proc. Amer. Math. Soc. 144(5) (2016), 2109–2120.Google Scholar
Shimomura, T.. Cantor proximal systems with topological rank 2 are residually scrambled. Preprint, 2016, arXiv:1602.01568.Google Scholar