Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T03:35:30.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic independence of multipliers of periodic orbits in the space of polynomial maps of one variable

Published online by Cambridge University Press:  15 December 2014

IGORS GORBOVICKIS
IGORS GORBOVICKIS*
Affiliation:
Department of Mathematics, University of Toronto, Room 6290, 40 St. George Street, Toronto, Ontario, Canada M5S 2E4 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the space of complex polynomials of degree 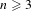$n\geq 3$ with 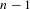$n-1$ distinct marked periodic orbits of given periods. We prove that this space is irreducible and the multipliers of the marked periodic orbits, considered as algebraic functions on that space, are algebraically independent over 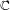$\mathbb{C}$. Equivalently, this means that at its generic point the moduli space of degree-$n$ polynomial maps can be locally parameterized by the multipliers of 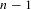$n-1$ arbitrary distinct periodic orbits. We also prove a similar result for a certain class of affine subspaces of the space of complex polynomials of degree $n$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1156 - 1166
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bousch, T.. Sur quelques problèmes de dynamique holomorphe. PhD Thesis, Université de Paris-Sud, Centre d’Orsay, 1992.Google Scholar
Epstein, A.. Transversality in holomorphic dynamics. http://homepages.warwick.ac.uk/ mases/Transversality.pdf.Google Scholar
Gorbovickis, I.. Some problems from complex dynamical systems and combinatorial geometry. PhD Thesis, Cornell University, 2012.Google Scholar
Gorbovickis, I.. Algebraic independence of multipliers of periodic orbits in the space of rational maps of the Riemann sphere. Moscow Math. J. (2014), to appear, arXiv:1401.4713.Google Scholar
Lau, E. and Schleicher, D.. Internal addresses in the Mandelbrot set and irreducibility of polynomials. 1994, http://www.math.sunysb.edu/preprints/ims94-19.pdf.Google Scholar
Manes, M.. Moduli spaces for families of rational maps on ℙ1. J. Number Theory 129(7) (2009), 1623–1663.Google Scholar
McMullen, C.. Families of rational maps and iterative root-finding algorithms. Ann. of Math. (2) 125(3) (1987), 467–493.Google Scholar
Milnor, J.. Remarks on iterated cubic maps. Experiment. Math. 1(1) (1992), 5–24.Google Scholar
Milnor, J.. Geometry and dynamics of quadratic rational maps. Experiment. Math. 2(1) (1993), 37–83, with an appendix by the author and Lei Tan.Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Morton, P.. Galois groups of periodic points. J. Algebra 201(2) (1998), 401–428.CrossRefGoogle Scholar
Schleicher, D.. Internal addresses in the Mandelbrot set and irreducibility of polynomials. PhD Thesis, Cornell University, 1994, ProQuest LLC, Ann Arbor, MI.Google Scholar
Sugiyama, T.. The moduli space of polynomials of one complex variable. Preprint, 2007, arXiv:0708.2512.Google Scholar
Zarhin, Yu. G.. Polynomials in one variable and ranks of certain tangent maps. Math. Notes 91(4) (2012), 508–516.Google Scholar
Zarhin, Yu. G.. One dimensional polynomial maps, periodic points and multipliers. Izv. Math. 77(4) (2013), 700–713.Google Scholar