Article contents
Algebraic geometry of the center-focus problem for Abel differential equations
Published online by Cambridge University Press: 06 November 2014
Abstract
The Abel differential equation 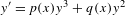 $y^{\prime }=p(x)y^{3}+q(x)y^{2}$ with polynomial coefficients
$y^{\prime }=p(x)y^{3}+q(x)y^{2}$ with polynomial coefficients 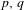 $p,q$ is said to have a center on
$p,q$ is said to have a center on  $[a,b]$ if all its solutions, with the initial value
$[a,b]$ if all its solutions, with the initial value 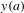 $y(a)$ small enough, satisfy the condition
$y(a)$ small enough, satisfy the condition 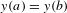 $y(a)=y(b)$. The problem of giving conditions on
$y(a)=y(b)$. The problem of giving conditions on  $(p,q,a,b)$ implying a center for the Abel equation is analogous to the classical Poincaré center-focus problem for plane vector fields. Center conditions are provided by an infinite system of ‘center equations’. During the last two decades, important new information on these equations has been obtained via a detailed analysis of two related structures: composition algebra and moment equations (first-order approximation of the center ones). Recently, one of the basic open questions in this direction—the ‘polynomial moments problem’—has been completely settled in Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728]. In this paper, we present a progress in the following two main directions: first, we translate the results of Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728] into the language of algebraic geometry of the center equations. Applying these new tools, we show that the center conditions can be described in terms of composition algebra, up to a ‘small’ correction. In particular, we significantly extend the results of Briskin, Roytvarf and Yomdin [Center conditions at infinity for Abel differential equations. Ann. of Math. (2)172(1) (2010), 437–483]. Second, applying these tools in combination with explicit computations, we start in this paper the study of the ‘second Melnikov coefficients’ (second-order approximation of the center equations), showing that in many cases vanishing of the moments and of these coefficients is sufficient in order to completely characterize centers.
$(p,q,a,b)$ implying a center for the Abel equation is analogous to the classical Poincaré center-focus problem for plane vector fields. Center conditions are provided by an infinite system of ‘center equations’. During the last two decades, important new information on these equations has been obtained via a detailed analysis of two related structures: composition algebra and moment equations (first-order approximation of the center ones). Recently, one of the basic open questions in this direction—the ‘polynomial moments problem’—has been completely settled in Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728]. In this paper, we present a progress in the following two main directions: first, we translate the results of Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728] into the language of algebraic geometry of the center equations. Applying these new tools, we show that the center conditions can be described in terms of composition algebra, up to a ‘small’ correction. In particular, we significantly extend the results of Briskin, Roytvarf and Yomdin [Center conditions at infinity for Abel differential equations. Ann. of Math. (2)172(1) (2010), 437–483]. Second, applying these tools in combination with explicit computations, we start in this paper the study of the ‘second Melnikov coefficients’ (second-order approximation of the center equations), showing that in many cases vanishing of the moments and of these coefficients is sufficient in order to completely characterize centers.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 7
- Cited by


