1. Introduction
AI systems are being used for a rapidly increasing number of important decisions. Many of these systems are “black boxes”: their functioning is opaque to the people affected by them, and in many cases even to the people developing and deploying them. This opacity is due to the complexity of the function or model that the AI system implements, and to the fact that these systems are trained using machine learning techniques, rather than being explicitly programmed. For instance, Deep Neural Networks (DNNs) are the type of model most responsible for recent advances in AI capabilities, including in translation, visual recognition, and navigation (LeCun et al. Reference LeCun, Bengio and Hinton2015). However, DNNs are famously complex and difficult to understand, even for those who build them.
The opacity of black box systems is undesirable. It makes them difficult to evaluate for accuracy and fairness, it makes them less trustworthy, and it makes it harder for affected individuals to seek recourse for undesirable decisions. To deal with these problems, a growing body of literature in computer science seeks to alleviate this opacity. The goal of opacity alleviation is often talked about in terms of transparency, interpretability, and explainability. However, it is often lamented that there is little agreement on the meaning of these terms (Lipton Reference Lipton2018; Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020; Krishnan Reference Krishnan2020). This has resulted in disputes about the goals of this project, what it would mean to achieve these goals, and how these goals might be used to craft concrete regulations.
In this paper, I argue that transparency, interpretability, and explainability should all be defined in terms of the fundamental concept of understanding. On this understanding-based account, for an AI system to be transparent and interpretable is for it to be understandable to the relevant stakeholders: the developers, those deploying the system, and (most importantly) those affected by the system's decisions. A system is explainable when it is accompanied by an explanation that puts stakeholders in a position to understand why that decision was made. This conceptualization allows us to appeal to the epistemology and philosophy of science literature regarding understanding in order to help clarify what it would mean to successfully alleviate the opacity of AI systems. The understanding-based account also helps to clarify the relationship between alleviating opacity and respecting people's rights to (normative) explanation.
An immediate benefit of the understanding-based account of opacity alleviation is that it helps defuse a prominent objection to post hoc explainable AI (XAI) methods. XAI methods attempt to explain black box systems (e.g., DNNs) by building a second “explanation” model. These methods are “post hoc” because the explanation model is used to explain the black box system after its use, without altering the original system. The explanation model consists of a simpler type of model, one that is more interpretable (i.e., understandable) to humans than the original black box model. For instance, the Linear Interpretable Model-agnostic Explanations method, known as LIME, is a feature importance-based XAI method (Ribeiro et al. Reference Ribeiro, Singh and Guestrin2016). LIME builds simple linear equation models that approximate the behavior of black box models for a constrained set of circumstances. The resulting LIME model is then used to make inferences about the behavior of the original black box model's decision. Specifically, it is used to identify which features of the individual being classified were the most important in determining the original model's decision.
Philosophers and computer scientists have raised an objection to the use of post hoc XAI methods such as LIME, which I call the rationalization objection. This objection is based on two features of XAI methods: (a) they function to compute a very different algorithm than the black box models they are used to explain; and (b) they are imperfectly reliable or faithful, i.e., they sometimes make different predictions than the original model. For these reasons, objectors have argued that LIME (and other XAI methods) cannot provide genuine explanation and understanding, but are instead inherently misleading. While the rationalization objection is not the only difficulty XAI methods face (Krishna et al. Reference Krishna, Han, Gu, Pombra, Jabbari, Wu and Lakkaraju2022), I take it to be the most pressing in-principle objection.
I argue, however, that XAI methods such as LIME function in much the same way as idealized scientific models. This is a kind of models-of-models view of XAI systems. Idealizations are features of a scientific model that misrepresent the model's target phenomena. It is a consensus view in the epistemology of understanding that idealized models can be used to gain a high-degree of understanding (Strevens Reference Strevens, Grimm, Baumberger and Ammon2016; Baumberger et al. Reference Baumberger, Beisbart, Brun, Baumberger and Ammon2017; Elgin Reference Elgin2017; Potochnik Reference Potochnik2017; Sullivan and Khalifa Reference Sullivan and Khalifa2019; Grimm Reference Grimm2021). If XAI methods produce models that serve as idealized scientific models of opaque AI systems, this undermines the rationalization objection to XAI. Neither perfect fidelity, nor computing a similar algorithm, are necessary conditions for generating adequate understanding of the original model.
Here is the plan for the paper: first, I will offer some background on black box models using Deep Neural Networks as a primary example (§2). Second, I will discuss the literature on alleviating opacity via transparent, interpretable, and explainable AI (§3), and suggest that the concept of understanding should be central to these projects (§4). Then, I will discuss the rationalization objection to post hoc XAI methods (§5). In order to respond to this objection, I will discuss the importance of idealization to understanding (§6). Finally, I will argue that recognition of the importance of idealization offers a response to the rationalization objection to XAI (§7).
2. Black Boxes: Opacity and Deep Neural Networks
Many of the most exciting advancements in artificial intelligence capabilities have come through the use of “deep learning” systems. Deep learning involves deep neural networks (DNNs): algorithms that are loosely inspired by the way neurons process information in brains.Footnote 1 DNNs are behind advances in image classification, translation, language production, and gaming systems (LeCun et al. Reference LeCun, Bengio and Hinton2015; Russell and Norvig Reference Russell and Norvig2020). DNNs are not the only kind of AI system that is opaque in the sense(s) at issue, i.e., that we would call a “black box.” However, I will focus on DNNs as a primary example.Footnote 2
To simplify discussion, I will focus on DNNs that are used for classification tasks. Classification systems apply labels to an input (Russell and Norvig Reference Russell and Norvig2020: 714). For instance, a classifier might be trained to recognize images of cats. It does so by taking as input some image, then as output applying the label “cat” or “non-cat.” In reality, there is some relation between a picture having particular features and the probability that the picture depicts a cat. A classification system is designed to represent or model this relation, i.e., to attribute the label when there is a high probability of the picture being a cat, based on the features of the picture. For this reason, a particular classification algorithm is called a model (or hypothesis) as it is meant to model the actual relation in the world.
A DNN is a model that computes a complicated, non-linear function. A DNN is composed of individual units (see Figure 1), connected to one another in a layer structure. Each unit receives input signals (x i) along its connections, and each connection is assigned a weight (w ij). A unit has a particular activation function: a function that receives the weighted sum of input signals (net j), and if that sum is above a certain threshold (θ j), it outputs an activation signal of a certain strength (o j). The signal passed on by the activation function of a unit can then serve as input for another unit of the DNN, or it can serve as part of the DNNs output.

Figure 1. A unit or artificial neuron. From “Artificial Neuron Model” by Chrislb. Wikimedia Commons (https://commons.wikimedia.org/wiki/File:ArtificialNeuronModel.png). CC BY-SA 3.0.
DNNs are arranged in layers (see Figure 2). A layer is a set of units that are not connected to each other, but only to units in other layers. Units in the input layer of a model receive information about the input to be classified, e.g., values representing pixels or areas of a picture. Output layers transmit the classification, the output of the model. In a classification system, there is typically one unit representing each label. In between the input and output layers there are hidden layers, so called because they only interact with other units within the system. What makes a deep neural network “deep” is that it contains at least two hidden layers. DNNs are trained using machine learning techniques, rather than explicitly programmed. This training involves changing the weights the strength of the connections between units – whenever the model makes a mistake on its training data. DNNs can be surprisingly accurate for the task on which they are trained, and moreover this accuracy often scales with the size of the network.
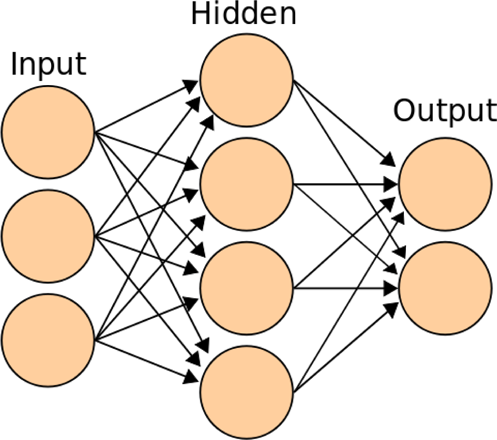
Figure 2. A simple Deep Neural Network structure. From “Artificial Neural Network” by Cburnett. Wikimedia Commons (https://commons.wikimedia.org/wiki/File:Artificial_neural_network.svg). CC BY-SA 3.0.
There are two crucial things to take away from this brief description of DNNs. First, DNNs begin with simple calculations (the units) as components, but string them together into enormous and extremely complex network structures. Some cutting-edge, contemporary deep learning systems can have hundreds of billions of connections (Brown et al. Reference Brown, Mann, Ryder, Subbiah, Kaplan and Dhariwal2020). Second, DNNs are trained rather than programmed. Both of these features contribute to their opacity.
There are three main types of opacity relevant to DNNs and other complex AI models (Burrell Reference Burrell2016). First, some models are part of proprietary systems: the owners and developers of the system do not release their code because it is a trade secret. Many systems that have enormous impact on society are opaque in this sense, e.g., Facebook's newsfeed algorithm, Youtube's recommendation algorithm, and sentencing recommendation systems in the criminal justice system (e.g., COMPAS; Angwin et al. Reference Angwin, Larson, Mattu and Kirchner2016).
A second type of opacity concerns stakeholders other than developers. Even much simpler kinds of algorithms than DNNs require a significant level of technical knowledge to comprehend. There will be many stakeholders of such systems that won't have this level of technical knowledge. An AI system will be opaque to these stakeholders unless some effort is made to offer more accessible explanations.
A third type of opacity is opacity that obtains even for experts and the developers of the model themselves.Footnote 3 The basic idea is this: the programmers of a DNN know all of the fundamental details about the way the system works. They know how the units function, how the units are strung together, and what kind of training algorithm was deployed to determine the connection weights. Yet there is still some sense in which they don't know why the system does what it does, or why it is reliable at its task (Russell and Norvig Reference Russell and Norvig2020).
DNN models compute functions that are highly complex and non-linear. They also track features of the world that are complex and higher-level. Crucially, it is often unclear what contribution each unit, and each layer, is making to the way the system tracks the properties in the world it is classifying. In fact, in many cases there is a trade-off between accuracy and decomposability, where the latter term refers to the ability to break down a DNN model into parts which track recognizable features, or otherwise contribute to the computation in a way that is discrete and interpretable to humans (Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020). Sullivan (Reference Sullivan2022) calls this type of opacity link uncertainty: we do not know the link between the model's components and features of the world it is tracking. However, even if we were able to obtain link certainty – i.e., learn which features of the world a model is tracking and the role each unit and layer plays in tracking those features – this would not entirely alleviate the system's opacity. This is because the features of the world being tracked by the system are very likely to be complex and higher-level, and so will appear inscrutable or gerrymandered.
The opacity of DNNs poses a problem because it interferes with a variety of desiderata for AI systems. Opaque systems are less likely to be trusted, accepted, and used by stakeholders (Ribeiro et al. Reference Ribeiro, Singh and Guestrin2016; Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020). Opaque systems can be more difficult to debug and improve (Rudin Reference Rudin2019; Babic et al. Reference Babic, Gerke, Evgeniou and Cohen2021). Lacking adequate knowledge and understanding of why the system does what it does makes the system less trustworthy, and makes it seem less trustworthy. Moreover, opacity limits the ability of individuals to contest decisions made by black box AI systems (Mittelstadt et al. Reference Mittelstadt, Russell and Wachter2019), to seek recourse (Venkatasubramanian and Alfano Reference Venkatasubramanian and Alfano2020), or to achieve a better outcome the next time they receive an algorithmic decision (Wachter et al. Reference Wachter, Mittelstadt and Russell2017; Vredenburgh Reference Vredenburgh2022). Therefore, we have strong reasons to eliminate or alleviate the opacity of black box models. Moreover, if there is a right to explanation, as suggested by the EU's GDPR law (Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020; Vredenburgh Reference Vredenburgh2022), or if we owe a normative explanation (justification) to people for their treatment by AI, then alleviating opacity may be a moral obligation when using such AI systems.
3. Transparent, Interpretable, and Explainable AI
There are three main concepts or terms that are commonly used when discussing the goal of alleviating opacity: transparency, interpretability, and explainability. We can call the subfield of AI research that studies opacity alleviation TIE for ease of reference. A common worry about TIE discussions is that there is little agreement about how these terms (and their associated concepts) are to be used and understood (Doshi-Velez and Kim Reference Doshi-Velez and Kim2017; Guidotti et al. Reference Guidotti, Monreale, Ruggieri, Turini, Giannotti and Pedreschi2018; Lipton Reference Lipton2018; Murdoch et al. Reference Murdoch, Singh, Kumbier, Abbasi-Asl and Yu2019; Weller Reference Weller2019; Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020). This is sometimes taken as a reason to doubt the usefulness of TIE research (Krishnan Reference Krishnan2020) or its constituent concepts (Lipton Reference Lipton2018). I will argue that we can defuse these worries by defining these terms using the fundamental concept of understanding.
3.1. Transparency and Interpretability
Before offering a sketch of the understanding-based account of TIE, it will help to discuss the ways the terms are currently used. “Transparency” is used in at least three ways. The first treats it as simply the antonym of opacity: a system is transparent just when it is not opaque (Creel Reference Creel2020: 3). Second, the term is sometimes used to refer to inherently interpretable methods, while excluding post hoc XAI methods (Rudin Reference Rudin2019). Third, and perhaps most commonly, the term is used for systems whose code and development process are open and accessible to the public. That is, a system is transparent if it is not opaque due to its code being secret and proprietary to its owners.
Interpretability is most often treated as a “know it when you see it” property (Doshi-Velez and Kim Reference Doshi-Velez and Kim2017: 1). Essentially, interpretable systems are simpler models that seem more tractable, knowable, or understandable to humans. The term is typically applied to systems that use models of the same sort that humans can code explicitly, e.g., decision-trees, decision lists, linear models, and logistic regression (Lakkaraju et al. Reference Lakkaraju, Adebayo and Singh2020). Interpretability is most often discussed in terms of knowing how a system works (Murdoch et al. Reference Murdoch, Singh, Kumbier, Abbasi-Asl and Yu2019), being able to see how it functions, or being understandable or intelligible to a human (Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020). One feature taken to enhance interpretability is decomposability. A system is decomposable, in the relevant sense, when its functioning can be broken into simpler, discrete parts that serve specific, independent, and identifiable purposes in the system (Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020: 88). As I noted above, in DNN models there appears to typically be a tradeoff between decomposability and accuracy.
Some computer scientists and philosophers have argued that we should opt for “inherent interpretability”: that we should avoid opacity by only using interpretable models whose workings we already know. For instance, Rudin (Reference Rudin2019) argues that there is not always a tradeoff between accuracy and interpretability because, for many use cases, inherently interpretable models – such as decision trees or linear regression models – offer comparable accuracy to black box DNNs. Where this is true, we have strong reason to use models that are more easily understood by developers and other stakeholders. Many ML developers, however, take there to be a significant accuracy advantage to using DNN models for a variety of tasks, e.g., visual recognition, gaming AI, and translation (Lakkaraju et al. Reference Lakkaraju, Adebayo and Singh2020; McNeill Reference McNeill2021). And in such cases, there does seem to be a tradeoff between accuracy and interpretability (Morcos et al. Reference Morcos, Barrett, Rabinowitz and Botvinick2018; McNeill Reference McNeill2021).
3.2. Post Hoc XAI
“Explainability” is sometimes used interchangeably with “interpretability.” However, most often it refers to the project of post hoc explainable AI, or XAI. These are called “post hoc” because they provide explanations for the operation of a black box system after it has been used. Inherently interpretable systems are the very AI systems being used for the task; they are used instead of using some black box model. In contrast, XAI methods are meant to help with tasks where using an interpretable model instead of a DNN (or other black box model) would involve a significant loss of accuracy or efficiency.
XAI methods aim to explain why a black box model acted as it did. They involve using a second model, one that provides an explanation for why the original black box model made a particular classification (Guidotti et al. Reference Guidotti, Monreale, Ruggieri, Turini, Giannotti and Pedreschi2018; Lipton Reference Lipton2018; Arrieta et al. Reference Arrieta, Díaz-Rodríguez, Del Ser, Bennetot, Tabik, Barbado, Garcia, Gil-Lopez, Molina, Benjamins, Chatila and Herrera2020). For instance, when a DNN classifies an image as containing a cat, one could employ an XAI method to offer an explanation for why the DNN made that classification. The explanation model is a model that – in some sense – approximates the function of the original black box model. The explanation model is designed to be simpler and more interpretable. This typically means using model types that humans could in principle explicitly program, such as linear models, decision lists, and decision trees. The explanation model is then used to make inferences about how the original model functions.
XAI research is a new field, but it has already created a wide variety of approaches. Global XAI methods attempt to build explanation models that approximate the black box model's function in its full range of use; i.e., for all the kinds of input it can receive. Local XAI methods attempt to approximate the original model in a limited range of circumstances, as a way of explaining why a particular decision was made. These include feature importance methods, saliency maps, prototype methods, and counterfactual methods.Footnote 4
As a primary example, I will focus on one influential local XAI approach, a feature importance method called Linear Interpretable Model-agnostic Explanations, or LIME (Ribeiro et al. Reference Ribeiro, Singh and Guestrin2016). LIME identifies the features of an individual input that were most important in influencing a black box model's classification of that individual. It also measures the relative importance of each important feature, and identifies the label each feature made more probable. A list or visual display of this information is then presented to stakeholders as an explanation of the classification made by the original black box model.
LIME works by building a simple linear model that approximates the behavior of the original classifier (at least for individuals sufficiently similar to the input to be explained). The linear model build by LIME is then used to make inferences about the behavior of the original black box model that is being approximated. If the LIME model is influenced by a particular feature, we then infer that the original black box model was too. We can see LIME as building models-of-models: the explanation model built by LIME represents or models the original black box model. As I will argue below, we can think of this as being analogous (or even identical) to the way scientific models represent their target phenomena.
The LIME algorithm follows roughly this procedure: it takes the input from the classification outcome to be explained – e.g., an image of a cat labeled as a cat, or a loan application that was denied. It then repeatedly “perturbs” this original input to create a sample set of other possible inputs to the original model. For an image, this perturbation might involve obscuring portions of the image with gray. For a loan application, it may involve changing the credit score, debt total, or salary. LIME then calls the original black box method on each of these samples, i.e., it asks the original model how it would classify these synthetic samples. LIME then learns a simple linear model using these classified samples as supervised training data, paying the most attention to samples that have input that is most similar to the original.
Figure 3a illustrates the construction of a toy LIME model. Points in the space represent different possible inputs, the x and y axes represent distinct features, and the color of the background displays the applied label. The biggest cross is the initial input, the other crosses and dots represent synthetic samples, and their size represents how much importance they were given in building the LIME model. The LIME model is represented by the dotted line: inputs on either side receive different labels. Figure 3b represents an image presented to Google's Inception neural network, which classified it as containing a Labrador (with Pr = 0.21). Figure 3c shows a LIME explanation for Inception's output. The grayed-out sections are those LIME thinks were unimportant in driving Inception's decision.

Figure 3. Illustrating LIME in action (image amended from Ribeiro et al. Reference Ribeiro, Singh and Guestrin2016).
When things go well, the linear explanation model produced by LIME classifies each of the samples in the local area the same way the original black box model did. In the cat image case, this means that the LIME-produced model will classify as cat images all and only the same perturbed images as the original model does. In that case the explanation model is perfectly locally faithful (Lakkaraju et al. Reference Lakkaraju, Kamar, Caruana and Leskovec2019). Alternatively, the model might be highly locally faithful, if it classifies the vast majority of the samples in the same way as the original black box model. Clearly, some high degree of faithfulness is required, or we won't take the LIME model be successful in representing the original model. (If it is impossible to produce a decently faithful model, LIME indicates this to its user.)
Once LIME generates its simple linear model, this is used to create reports for communication to stakeholders. These reports indicate which features are important, and how important they are. For instance, in the cat image classification example, LIME produces an image as a report, one that obscures all the parts of the image except those that are considered important by the simple linear model (see Figure 3c for a similar example). For the loan application example, LIME can produce a histogram report, showing the relative importance of the different features of the application.
One clear benefit of LIME is that it can help users and developers of a black box model recognize when the model is paying attention to what are obviously the wrong features. This can help with avoiding problems of overfitting, i.e., where the model is accurate at classifying its training data but fails to generalize this accuracy to other inputs. For instance, Ribeiro et al. (Reference Ribeiro, Singh and Guestrin2016) point to an example in which a classifier is reliable at distinguishing images of wolves from images of huskies. However, LIME showed that the classifier is paying attention to parts of the image that show snow, not dog/wolf features. The system was using snow as a proxy for recognizing wolves, because of a coincidental correlation in its training data, a method that would clearly fail if applied to other image sets. Feature importance methods are also valuable in recognizing when a system is paying attention to features that it shouldn't be, morally speaking, e.g., if a loan application system places high importance on race or gender.
LIME is an influential and representative XAI method, and it is also clearly a target of the rationalization objection. So, I will continue to appeal to it as my primary example in what follows.
4. Understanding and TIE
The idea that there is a connection between explainability, interpretability, and understanding is intuitive, plausible, and inspires wide agreement.Footnote 5 However, there has been little attempt to apply insights from epistemology and philosophy of science regarding understanding to the discussion of TIE.Footnote 6 In addition, the ability of understanding to provide the keystone or fundamental notion for these discussions has often been overlooked. I want to suggest that taking the common use of understanding talk seriously helps to solve conceptual confusion and linguistic disputes within TIE research. Moreover, it enables a defense of XAI methods from the rationalization objection.
4.1. Understanding in Epistemology and Philosophy of Science
Understanding, like knowledge, is an attitude of a subject that involves a mental state component, a success condition, and a normative epistemic condition. There are several types of understanding.
Here, I will focus on explanatory understanding, also called understanding-why. Explanatory understanding concerns understanding why some proposition is true, e.g., “Michonne understands why the climate is warming” and “John understands why his loan was denied.” This type of understanding is plausibly what is at issue in TIE discussions, since we are concerned with explaining why an AI system made a particular classification.Footnote 7
There is a great deal of disagreement in epistemology about the nature of understanding, and its normative components. For one thing, there is disagreement over whether understanding is a form of knowledge, or can be reduced to that state. Despite this, there is significant agreement about many aspects of understanding. This agreement can offer guidance for TIE, and for XAI specifically. There is agreement, for instance, regarding the idea that understanding has both mental state and normative components; that it involves some mental representation or attitude as a vehicle; that it involves a justification condition; that it is not reducible to the subjective feeling of understanding (i.e., the “aha!” feeling); that understanding comes in degrees; and that some amount of inaccuracy or falsehood in the vehicle of understanding is compatible with genuine understanding.Footnote 8
On important point of agreement in the literature is that understanding comes in degrees (Baumberger et al. Reference Baumberger, Beisbart, Brun, Baumberger and Ammon2017; Grimm Reference Grimm2021; Hannon Reference Hannon2021). A scientist working on climate models will better understand why wildfires occur with greater frequency than a layperson will. Still, the scientist can provide an explanation (e.g., in terms of average temperature and drought) that will offer the layperson some significant degree of genuine understanding. Moreover, college students learning about Newtonian Mechanics gain some significant degree of genuine understanding of why objects fall to earth, despite the fact that the theory is strictly speaking false, or at least less accurate than General Relativity. Meanwhile, a professional physicist who works on relativity will have a greater understanding. Thus, a maximal degree of understanding is not required for being counted as possessing understanding.
Understanding is often taken to require grasping an explanation (or some other representation) of what is understood. There have been a variety of proposals about how to give a precise account of this admittedly metaphorical notion. Often, the idea is cashed out in terms of some sort of abilities. For instance, Hills (Reference Hills2015) gives an account of grasping in terms of cognitive control, where this amounts to having a set of abilities concerning the relationship between P and Q, where Q is a reason why P. These abilities involve being able both follow and offer explanations for P, and potential explanations for other nearby propositions. Elgin (Reference Elgin2017) suggests that grasping involves knowing how to exploit information provided by one's understanding. Potochnik (Reference Potochnik2017) treats grasping as ability to exploit information about causal patterns relevant to the object that is understood.Footnote 9
Understanding and explanation are intimately connected. Grasping an explanation is often taken to be crucial (or even necessary) for achieving understanding (Hills Reference Hills2015; Potochnik Reference Potochnik2017; Strevens Reference Strevens2013). As noted above, some have argued that understanding why P just is knowing an explanation for P (Baumberger et al. Reference Baumberger, Beisbart, Brun, Baumberger and Ammon2017; Khalifa Reference Khalifa2017; Grimm Reference Grimm2021). Others have suggested that explanations are not necessary, but are the typical vehicle for transmitting or sharing understanding (Potochnik Reference Potochnik2017). But there is agreement that a good explanation is one that can provide understanding (Baumberger et al. Reference Baumberger, Beisbart, Brun, Baumberger and Ammon2017; Grimm Reference Grimm2021; Hannon Reference Hannon2021).
A final point of agreement about understanding concerns its compatibility with idealization. While there is a great deal of disagreement about what this connection with idealization tells us about epistemic value, there is general agreement that idealized models can provide understanding. This will be crucial to the defense of XAI from the rationalization objection, and is discussed in detail in section 6.
For concreteness and ease of discussion, in the remainder of the paper I will adopt an account of understanding and explanation primarily inspired by Potochnik (Reference Potochnik2017), but also influenced by Hills (Reference Hills2015) and Elgin (Reference Elgin2017).
Understanding A subject understands why P if the subject grasps an explanation E of P, where • An explanation consists in information about causal patterns relevant to why P obtains. • A subject grasps an explanation E if the subject accepts E and has abilities to exploit and manipulate the causal pattern information it contains.
This account has both a mental state component in the form of acceptance, and an achievement component in the requirement of having certain abilities. The account here is simply a sufficient condition: it leaves open the possibility that there are other means of achieving understanding. This sufficient condition is adequate for defending XAI from the rationalization objection.
Following Potochnik, this account also adopts a pragmatic or communicative account of the nature of explanation.Footnote 10 On this account, explanations are acts of communication that convey information about causal patterns in order to facilitate understanding for a particular audience.Footnote 11 Potochnik appeals to Woodward's (Reference Woodward2005) interventionist or manipulability account of causation in describing causal patterns. The interventionist account models all causation on scientific experiments that hold fixed some variables while experimentally changing another. Suppose X and Y are variables representing properties in the world. If a specific surgical change (i.e., an intervention) to X produces a specific change to Y across a variety of circumstances, then X is a cause of Y. An intervention is a change to X that makes no changes to other variables that might sit between X and Y and mediate their relationship. A causal pattern is a regularity of this sort interventionist causal relationship. I will use Potochnik's notion of a causal pattern. However, the account here is compatible with other views about what would constitute a causal pattern.
On the theory of understanding on offer, grasping an explanation means having the ability to exploit or manipulate the information about causal patterns it contains. The account also treats understanding as fundamental: “The idea that scientific explanations are the means to generating scientific understanding also must be given pride of place in an account of explanation. The relationship between explanations and the cognitive needs of explainers must guide one's account of explanation” (Potochnik Reference Potochnik2017: 131).
This account of understanding exemplifies the points of agreement discussed above. It is also particularly apt for discussion of idealization, as Elgin and Potochnik's accounts are designed precisely to accommodate the importance of idealized models to understanding. But, as previously noted, there are a variety of other accounts compatible with the defense of XAI that I will offer.
4.2. Understanding as Fundamental to TIE
Here, I want to offer a brief and simple sketch of how understanding can be used to give a coherent and straightforward account of the various operative notions of TIE:
A model is interpretable for a stakeholder iff it is understandable by that stakeholder (to a sufficient degree).
A model is transparent to a stakeholder iff it is understandable to that stakeholder (to a sufficient degree).
A model is explainable to a stakeholder iff it is accompanied by an XAI method whose output provides an explanation that puts the stakeholder in a position to understand why the system made the decision it did.
This account of the main concepts and terms of TIE has two primary benefits. First, it provides a unified, coherent conceptual framework for TIE discussions, eliminating the ambiguity and potential for talking past one another discussed above. This defuses worries that there is no way to salvage TIE discussions from conceptual confusion (Krishnan Reference Krishnan2020). The second benefit is that it makes explicit the fundamental importance of understanding to these concepts, and allows insights from the epistemology and philosophy of science literature regarding understanding to be applied to the TIE literature. Sections 5–7 present a third benefit of this application in responding to the rationalization objection. Before moving on to that discussion, I will note several additional benefits.
The first additional benefit is offering a unified account of how to deal with all three types of opacity identified by Burrell (Reference Burrell2016), as discussed in section 2. Each kind of opacity involves the inability of some stakeholders to understand the model in question. The first involves a lack of such ability due to information about proprietary systems being intentionally hidden or obscured. The second involves some stakeholders, like laypeople and non-technical policy-makers, being unable to understand the system's decisions. The third involves the inability to understand the model for anyone, even the developers, due to the model's complexity and inherent human cognitive limitations. In each case, what is lacking for the stakeholders in question is an adequate epistemic position to enable understanding.
A second benefit of appealing to understanding is that it helps clarify the stakeholder-sensitivity of TIE notions. What it takes for a system to be interpretable depends on who needs to be able to interpret, i.e., understand, the system. Different stakeholders will have different expertise, background domain knowledge, and fluency with the relevant technology. It has been noted by a variety of philosophers and computer scientists that interpretability or explainability needs to be made available for all the stakeholders affected by or taking part in the use of algorithmic decision-making (Preece et al. Reference Preece, Harborne, Braines, Tomsett and Chakraborty2018; Mittelstadt et al. Reference Mittelstadt, Russell and Wachter2019; Kasirzadeh Reference Kasirzadeh2021).
A third benefit is the additional guidance the account can provide for evaluating models for interpretability and for evaluating XAI methods for achieving explainability. As noted above, understanding is both a mental state and a cognitive achievement. In other words, there is a normative component and a success condition associated with understanding. Discussions of what success and normative requirements are necessary for achieving understanding can provide guidance regarding what it takes for an inherently interpretable model, or XAI method, to be successful in a particular use. For instance, many have suggested that coherence is a key epistemic requirement for achieving understanding (Kvanvig Reference Kvanvig2003; Elgin Reference Elgin2017; Potochnik Reference Potochnik2017). This suggests that XAI methods should produce outputs that will increase the coherence of stakeholders’ beliefs about how a black-box model works. Evaluation of TIE methods may thus be improved by appeal to understanding.
A fourth benefit of the understanding account is that it helps clarify the relationship between present technical efforts to develop interpretable and explainable AI, and the ethical and political goals of such projects. As I noted at the outset, one of the primary reasons people are concerned about opacity is that opacity undermines the moral legitimacy of using AI systems. Opaque systems are less trustworthy. Moreover, it is generally acknowledged that stakeholders and decision subjects are owed a justification, or normative explanation, for their treatment. If a decision deprives a person of a loan, a job, or their freedom, they are owed an explanation for this. As several philosophers have noted, the relevant sense of “explanation” here is different than we have so far been concerned with (Kasirzadeh Reference Kasirzadeh2021; Vredenburgh Reference Vredenburgh2022). In this sense, “explanation” refers to the moral reasons for a subject's treatment. This idea is plausibly what is driving claims of a “right to an explanation,” e.g., in the EU's General Data Protection law (Vredenburgh Reference Vredenburgh2022).
The understanding account of TIE can help to clarify how TIE efforts may relate to, and promote, this goal of providing normative explanations. Successfully providing the normative explanation – the moral reasons – for a decision requires the reasons given to be true. Moreover, the subject must be in a position to understand the explanations given. Suppose we explain to a loan applicant that they did not receive a loan because their income was too low, which indicates they would risk default. For that to be a genuine normative explanation, it had better be true that this is what drove the decision. If the decision was actually based on something else, we have failed to respect the applicant's right to an explanation. Similarly, we fail if the explanation does not put them in a position to understand. In other words, there are both accuracy and understanding conditions on normative explanation. According to the understanding account, TIE projects – including both inherently interpretable systems and XAI methods – aim to facilitate genuine understanding. This ensures both the accuracy and understanding conditions of normative explanation are met. Relatedly, TIE projects can ensure we recognize when there is no good normative explanation for a decision subject's treatment (Venkatasubramanian and Alfano Reference Venkatasubramanian and Alfano2020; Vredenburgh Reference Vredenburgh2022). In that case, TIE can help achieve recourse for people who have been treated in an unjust way.Footnote 12
Each of the foregoing benefits merits additional discussion, which I intend to pursue in future work. In the remainder of this paper, I turn to another benefit of the account: a defense of XAI methods from the rationalization objection.
5. The Rationalization Objection to XAI
There is a suspicion among some computer scientists and AI ethicists that there is something amiss with post hoc XAI methods such as LIME (Rudin Reference Rudin2019; Babic et al. Reference Babic, Gerke, Evgeniou and Cohen2021). The suspicion is that XAI methods do not provide an explanation for black box models at all, but instead provide a mere rationalization. As Babic et al. (Reference Babic, Gerke, Evgeniou and Cohen2021) put it:
Explainable AI/ML (unlike interpretable AI/ML) offers post hoc algorithmically generated rationales of black-box predictions, which are not necessarily the actual reasons behind those predictions or related causally to them. Accordingly, the apparent advantage of explainability is a “fool's gold” because post hoc rationalizations of a black box are unlikely to contribute to our understanding of its inner workings. Instead, we are likely left with the false impression that we understand it better. We call the understanding that comes from post hoc rationalizations “ersatz understanding.” (Babic et al. Reference Babic, Gerke, Evgeniou and Cohen2021: 285)
This is the rationalization objection. The primary thrust of this worry is that XAI methods produce explanation models that function differently than the original black box models they approximate, and that are imperfectly faithful to the original model. As a result, the XAI methods fail to produce explanations that facilitate genuine understanding. Instead, they provide misleading rationalizations that result in “ersatz understanding.”
I think the best version of the rationalization Objection is the following argument:
P1 XAI explanations consist in models that do not compute the same function as the original black box model.
P2 XAI explanations consist in models that are imperfectly accurate in representing the original black box model; i.e., the explanation model is imperfectly faithful.
P3 If an XAI explanation (a) does not involve the same computed function as the original model and (b) does not offer perfect faithfulness to the original model, then it probably does not provide a significant degree of understanding.
C Therefore, XAI explanations do not provide a significant degree of understanding.
Notice that the conclusion and normative premise are weaker than suggested by Rudin (Reference Rudin2019) and Babic et al. (Reference Babic, Gerke, Evgeniou and Cohen2021). Specifically, this version of the conclusion does not claim that the understanding provided is “ersatz,” merely that it is too weak a degree of understanding to be significant or valuable. In particular, we can understand this as meaning it is too insignificant to serve the purposes XAI methods are meant to serve. I think this is the strongest version of the objection, as its premises are easier to defend and its conclusion would show the inadequacy of XAI methods.
The first two premises of the rationalization objection argument are clearly true. XAI models do work differently than the models they are meant to explain. This difference is the very reason they are used. LIME, for instance, uses a simple linear model. LIME models are also decomposable, in that the effect of each feature on the classification is determined by a parameter of the linear equation. But as we also noted above, high-accuracy DNNs often do not have those features. A DNN computes a complex, non-linear model, and highly accurate ones are not decomposable. Thus, LIME models compute very different functions than a DNN.
Moreover, XAI models are imperfectly faithful: they are imperfectly reliable at replicating the classifications made by the original black box model. This unfaithfulness is an essential feature of XAI methods. If an XAI method produces an interpretable explanation model that perfectly reproduces the performance of the black box model, then it would have equal accuracy to the black box model, and the need for the black box model would be obviated. In the case of many black box models like the DNNs discussed above, this level of accuracy is impossible.
Thus, since the first two premises must be granted, I will defend XAI from the rationalization objection by denying premise 3.
6. Idealization and XAI
Premise 3 of the rationalization objection is a conditional, so to show it is false, I will argue that the two conditions of its antecedent can be satisfied while its consequent is false. In other words, I will argue that some XAI models (a) function differently than the original black box model and (b) are imperfectly faithful, and yet some uses of XAI methods can be expected to provide a significant degree of understanding. The crucial move here is to argue that XAI models are relevantly similar to scientific models.
Scientific models can generate explanations that produce significant understanding, despite deliberately misrepresenting their target phenomena. The deliberate misrepresentations in scientific models are known as idealizations. I will argue that XAI methods can similarly be seen as idealized models. The ways they misrepresent the functioning of black box models (like DNNs) are also idealizations (at least in cases where things go well). I support this by discussing three features of idealizations that are both benefits of idealization, and signs that the misrepresentation in question is an idealization rather than a mere distortion. I argue that the ways a LIME model differs from the DNN it approximates can be seen as idealizations, as these differences constitute misrepresentations that have each of the three features. When a LIME model has these features, it can promote significant and genuine understanding, despite misrepresenting the original black box model. Hence, P3 is false.
Below, I defend the crucial premise that LIME models are relevantly similar to idealized scientific models.Footnote 13
6.1. Idealized Scientific Models
For our purposes, we can understand a scientific model as a representation of some target phenomena. A model provides an explanation for that target, and is associated with a theory of that target. We can think of a model as a representation that encodes information about the causal patterns relevant to producing the target phenomena. This information can then be used to offer (communicative) explanations.Footnote 14
An enormous number of scientific models include idealizations. There are idealizations used in models in every field of scientific inquiry (Downes Reference Downes2020). An idealization is an aspect of a model that is false (Elgin Reference Elgin2017); that represents its target as-if it were other than it is (Potochnik Reference Potochnik2017). In other words, idealizations are features of a model that represent the target phenomena inaccurately.Footnote 15
One commonly discussed example of idealization is Boyle's ideal gas law: PV = nRT.Footnote 16 The law relates the pressure (P) and volume (V) of a gas to the number of molecules it contains (n) and it's temperature (T) using the “ideal gas constant” (R). Crucially, the law is part of a statistical mechanics model that represents the gas as if it has features it plainly does not. In particular, it represents the gas as though it was made up of molecules that don't interact with one another. As Elgin (Reference Elgin2004: 118) puts it, “The ideal gas law represents gas molecules as perfectly elastic spheres that occupy negligible space and exhibit no mutual attraction. There are no such molecules …”
The relationship between the objects and properties described by the ideal gas law does not hold in full generality. Nor is the law perfectly accurate. Its predictions are roughly accurate when certain assumptions are true, but far from accurate otherwise. Moreover, the way the law calculates the pressure and volume values involves depicting causal relations between the molecules to be fundamentally different than the actual causal relations in the world. According to the law, there are no interactions between molecules. But of course there are such interactions. Thus, the law represents a very different relation between these features than how the actual physical forces determine those features. (Note the similarities here to the premises of the rationalization objection).
There are more accurate ways of depicting these relationships than the ideal gas law. In particular, the law can be amended by adding new terms to the equation to depict the interactions between different molecules, resulting in the van der Waals equation (Mizrahi Reference Mizrahi2012: 243; Potochnik Reference Potochnik2017: 27; Sullivan and Khalifa Reference Sullivan and Khalifa2019: 677). The van der Waals equation is more accurate across a wider range of circumstances than the ideal gas law. It is plausibly closer to the truth, as it involves fewer misrepresentations. Despite this, the ideal gas law is still useful for a variety of purposes. It is much less complex and so is easier to calculate. Its results are close enough to the truth among a wide range of circumstances, and the limits of those circumstances (the “boundary conditions”) are well-understood. It seems to capture a genuine regularity, i.e., a causal pattern, even if that regularity is limited to certain circumstances and admits of exceptions. Moreover, it seems plausible that someone who learns the ideal gas law in school gains some new understanding of the behavior of gases that they did not have before.
Potochnik (Reference Potochnik2017) offers another example of an idealized model that includes even more significant departures from the truth: evolutionary game theory models of altruistic bat behavior using iterated prisoners’ dilemmas.Footnote 17 Vampire bats must feed every night. If one bat is unsuccessful in its hunt, other bats will give feed it regurgitated blood from their own hunt. This altruistic sharing behavior is an odd one to have evolved through competitive natural selection. Wilkinson (Reference Wilkinson1984) showed that modeling this sharing behavior as an iterated prisoners’ dilemma helps to explain how it could evolve. A reciprocal or tit-for-tat sharing strategy leads to better payouts for each bat in the long run, because other bats who adopt this strategy will also get better results, and so the behavior will spread through the population.
However, the game-theoretic model of bat altruism involves idealizations that depart from reality in extreme ways. For instance, the models in question represent the interactions as always being between two individual bats, when they are not. More significantly, the model assumes that “reproduction is asexual and that the population size is infinite, which together ensure a perfect relationship between a trait's success and its prevalence in the population” (Potochnik Reference Potochnik2017: 64). Not only are these large departures from reality no impediment to understanding, Potochnik suggests, they are in fact necessary for the model to display the causal pattern that it does. The idealizations are necessary for us to be able to pick out the particular causal pattern we are interested in, despite the enormous number of other potentially confounding factors.
These two examples will help to illustrate the three features of idealization I want to focus on, and to illustrate the analogy between idealized scientific models and XAI models.
6.2. Benefits and Signs of Idealization
Potochnik (Reference Potochnik2017) emphasizes that one of the features of science that leads to the use of idealized models is complexity. The world is filled with extremely complex systems. They are complex in that there are an enormous variety of features which are causal difference-makers to their behavior. That is, these systems contain a huge variety of causal patterns. For instance, macroeconomics attempts to understand why recessions occur. The number of relevant features that could potentially make a difference to this is astronomical. Similarly, cognitive neuroscientists attempting to understand the human nervous system must contend with an enormous number of variables concerning, e.g., ion channels, cell membranes, white matter, gray matter, hormones, neurotransmitters, dendrite connections, axon length, and the enormous variety of external stimuli to the nervous system.
Scientific inquiry aims to understand these complex systems. At the same time, it's generally acknowledged that scientific theories and models are better insofar as they are simple and generalizable. Scientific models are tools that we use to both understand and manipulate the world. To be useful for both of those purposes, they must be simple enough to comprehend, and they must apply to a wide range of phenomena. These goals are often in direct conflict with the goal of accurately representing a complex system. For complex systems, there is little hope that a short list of simple, universally generalized laws will provide a fully accurate picture of the phenomena. Rather, any adequately simple model will involve idealizations: aspects of the model that represent the world other than it is.
Scientific models contain information about causal patterns in their target phenomena. This is what makes them useful for providing the kind of explanations needed to promote understanding. Following Potochnik (Reference Potochnik2017), causal patterns are not a full causal history, nor need they be maximally informative. Rather, they contain limited information about domain-specific generic regularities that admit of exceptions. This is necessary for the causal patterns to be useful to humans: they need to be simple rules and patterns in order to be comprehended and used, despite the fact that they are part of enormously complex systems in the world.
Idealizations are used deliberately in scientific models in a variety of ways meant to help explain complex systems. These idealizations have benefits for promoting understanding. I will highlight three such benefits that are particularly helpful for thinking about XAI: The first is simplification: idealizations ensure that the models themselves are simple enough to be intelligible to a subject (de Regt and Dieks Reference de Regt and Dieks2005). The second is flagging: idealizations can be used to identify and highlight features which are not causal difference-makers (Strevens Reference Strevens, Grimm, Baumberger and Ammon2016; Elgin Reference Elgin2017). The third is focusing on specific causal patterns: idealizations can be used to suppress some genuine causal patterns, so that we can focus on those causal patterns we are interested in Elgin (Reference Elgin2017) and Potochnik (Reference Potochnik2017). In the next section, I discuss each of these three features in more detail, as I will argue they are also features of XAI models.
These three features help to make idealizations useful for scientific understanding by helping to deal with complexity. Moreover, they can help us to distinguish an idealization from a mere distortion or falsehood. That is, the presence of each of the three features in a scientific model provides defeasible evidence that the model is idealized, rather than merely mistaken. There are, of course, other familiar signs that a model is a successful one, e.g., empirical adequacy, novel predictive power, and theoretical virtues. If a model has these signs, and its misrepresentations provide simplification, flagging, and a focus on specific causal patterns, then we have good reason to conclude that it is an idealized model. In other words, deliberate use of misrepresentation is another useful (but defeasible) piece of evidence that the model is a successful, idealized model. Hence, its misrepresentations – its idealizations – make it more likely to be a model that provides understanding.
7. XAI Methods Produce Idealized Models
I want to suggest that XAI methods are like scientific models of the operation of black box AI systems. They represent the causal patterns within a particular target domain of complex phenomena: the target domain of black box AI models such as DNNs.
DNN models are opaque in part because they compute functions that are too complex for humans to follow. They also track higher-level features that are too complex for humans to parse. Thus, they are complex systems much like the ones represented by scientific models. Moreover, the XAI explanation models contain information about causal patterns in these black box models. For instance, a LIME model might represent certain parts of the causal patterns which led to an image being labeled a cat image, or to a loan application being denied. Specifically, it represents the features of the input that were important in leading to that classification, e.g., the cat shaped ears, or the debt/income ratio. These features are causal difference-makers in the behavior of the original system. This is analogous to the way Newtonian mechanics represents the causal patterns which led to a certain bridge staying up, or to a why a projectile landed where it did. The output of LIME facilitates communicative explanation: it consists in information about causal patterns and can be communicated to stakeholders to help them understand why a particular classification was made.
XAI explanation models represent black box models as if the black box models functioned in a way they do not. For instance, LIME produces linear models that represent the original model as if it calculated a linear equation. Explanation models also make predictions that are imperfectly faithful to the original model, particularly when the predictions are outside of a specific domain (this is particularly clear for local XAI methods like LIME). These points about XAI models show that the antecedent of P3 is satisfied. But they also make XAI models relevantly similar to idealized scientific models. Since idealized scientific models provide significant understanding, and XAI models are idealized in the same way as scientific models, XAI models can also provide genuine understanding. This analogy allows a response to the rationalization objection. It shows that its normative premise P3 is false.
To support the argument that XAI methods produce idealized models of black box systems, we need to look more closely at the analogy between XAI methods and idealized scientific models. I will focus on LIME as my primary example. What needs to be shown is that the way the linear models produced by LIME are idealized is relevantly similar to the way the scientific models are idealized. In particular, I will argue that the idealizations made by LIME confer the same benefits (and signs) of idealization identified in the last section: simplification for intelligibility, flagging non-difference-making features, and focusing our attention on relevant causal patterns. The presence of these features supports the claim that LIME makes idealizations, rather than mere distortions or falsehoods.
7.1. Simplification
Idealizations are used to make a model itself simpler, more tractable, and more understandable (Frigg and Hartmann Reference Frigg and Hartmann2020). In some cases, simplification merely makes a model more convenient and easier to use. This seems to be the case for present uses of the ideal gas law and Newtonian mechanics. However, in other cases the simplification is necessary for human understanding. Some phenomena are so complex, and involve so many actual causal difference makers, that a fully accurate model of the system would be literally incomprehensible to humans given our cognitive limitations. de Regt and Dieks (Reference de Regt and Dieks2005) call the ability to understand the model itself intelligibility. A model of an economy that included all of the difference-makers would be simply unintelligible to a human, and thus would provide little help in promoting explanatory understanding of the target phenomena.
Much like Boyle's ideal gas law, LIME models are much simpler than the actual causal structure of their target phenomena. The ideal gas law simplifies by leaving out calculations of the interactions of molecules that have vanishingly small effect on the behavior of the gas's pressure and volume. This makes calculating the ideal gas law equation much simpler and easier to understand than a more accurate model (e.g., the van der Waals equations) would be. Similarly, LIME involves calculating a linear model that is much simpler than a DNN.
That LIME produces simple, intelligible explanations should be very clear. LIME produces models consisting in linear equations that humans could compute with pen and paper (given adequate time). They are the same kind of algorithm that humans often explicitly program, and moreover they are the same kind of algorithm deployed directly by human decision-makers. The process by which LIME trains a model is very simple and well-understood by its developers (Ribeiro et al. Reference Ribeiro, Singh and Guestrin2016; Lakkaraju et al. Reference Lakkaraju, Adebayo and Singh2020). Even more importantly, the output of a LIME explanation model can be presented to stakeholders in very intuitive and easy to understand ways. These outputs typically involve either a simple histogram representing which features the original black box model takes to be important, or (in the case of models that take images as input) an image with only the most important areas of the photo visible (Figure 3c). Thus, LIME is very clearly designed to provide the benefit of simplification.
Of course, it should be conceded that mere distortions or mistakes can also lead to a model being more intelligible. Its trivial to create a very simple, obviously false model. So, merely showing that a misrepresentation makes a model simpler is not much support, by itself, for thinking that it is idealized. Rather, what I am suggesting is that, when deliberate misrepresentations make a successful model simpler, this is some evidence that the misrepresentations are idealizations rather than distortions. That is, combined with the facts that a model is empirically adequate, makes useful predictions, and has other theoretical virtues, the presence of deliberate, simplifying misrepresentations is some confirmation that the model is idealized.
7.2. Flagging
A second use of idealizations is to flag or make salient which features of a phenomena are causal difference-makers, and to clearly mark which features are not difference-makers. Elgin (Reference Elgin2004, Reference Elgin2017) and Strevens (Reference Strevens2008, Reference Strevens, Grimm, Baumberger and Ammon2016) both appeal to the idea that idealizations can make salient which features of a system are not causal difference-makers. Sullivan and Khalifa (Reference Sullivan and Khalifa2019) call this “flagging” the non-difference-making features. Flagging works by deliberately giving a variable in the model an obviously, flagrantly false value. This might include “zeroing out” the value of the variable, in a way that highlights the physical impossibility of what the model is claiming about its target, when read literally. The idea is that any competent user of the model will immediately recognize such a flagrant departure from possibility, and so recognize that the model-maker was trying to communicate the irrelevance of the value in question.
The ideal gas law deploys flagging idealizations (Strevens Reference Strevens2008, Reference Strevens, Grimm, Baumberger and Ammon2016). By setting the value of the effect of molecular interaction to zero, the model makes very salient that the interaction between molecules is not an important difference-maker to the gas's pressure. In circumstances where the ideal gas law is roughly accurate, this is useful information. It means that the complex calculations necessary to account for molecular interaction are not worth doing, as they won't make any relevant difference to the outcome. Thus, the flagging idealization has helped narrow down the relevant causal difference-makers. In this way, flagging helps to identify the actual, relevant causal patterns in the system the model is representing. It thus helps to promote understanding, by allowing for causal explanations to be more easily extracted and communicated.
LIME also involves flagging-type idealizations that can help us recognize non-difference-makers. This enables explanations which include causal patterns that are relevant to stakeholders, and so promotes their understanding. LIME outputs show which features of an input are important, and leaves out features which are unimportant. This is, of course, an idealization: the difference-makers are being identified using a linear approximation that does not work anything like the original model. So, the representation is false: some features which really are present in the calculations of the original DNN are left out, or their influence is represented falsely as being literally zero. However, by clearly setting the values to zero, this helps to identify which features are relevantly unimportant: which ones make no important difference to the outcome. When a LIME model shows that the model is only paying attention to the face-region of a cat image, it shows that the other regions of the image are not important difference-makers. In fact, it does so by graying out those regions entirely, i.e., flagrantly zeroing out their values. Similarly, if LIME shows that the system is paying attention only to background features of the image and not the parts with animals, this shows that the animal parts are not making a difference to how the system is classifying. This in turn allows the developers (or domain experts) to recognize when the system isn't working in the way that it should.Footnote 18
Thus, LIME models have the second beneficial feature of idealization. And the fact that a model deploys flagging idealizations improves its chance of producing a high degree of understanding. This shows that the failure of LIME to be perfectly accurate in its predictions, and its failure to reflect the underlying causal relations, is not reason to think it is less likely to generate understanding.
7.3. Focus on a Specific Causal Pattern
Given the enormous complexity of the physical systems being studied, these systems involve a vast number of different causal patterns. Idealizations facilitate understanding by allowing models to focus on specific causal patterns (Potochnik Reference Potochnik2017). Models idealized in this way leave out or distort genuine causal difference-makers and patterns, so that we can pick out causal patterns of interest to us.
The evolutionary game theory model of bat altruism provides a useful example of a model employing this kind of idealization. Recall that Wilkinson (Reference Wilkinson1984) appealed to an iterated prisoners’ dilemma model that represents a population of vampire bats as being infinite in size and reproducing asexually. These radical departures from reality allow the model to focus in on the influence of the long-term payoffs of reciprocity, by setting aside the complicating, potentially confounding features of contingent resource limitations and the chanciness of DNA rearrangement in sexual reproduction. These features are set aside not because they aren't difference-makers for the causal structure of the target phenomena. Instead, the features are set aside precisely because they are difference-makers, and modeling their influence would make it harder to recognize the more subtle causal patterns involving the long-term payoffs of reciprocally altruistic behavior. Evolutionary game theory models attempt to find general causal patterns which can provide understanding for why certain traits developed, despite the noise and complexity of ecological systems. This explains why the idealizations in such models so clearly depart from reality, e.g., representing bat populations as producing asexually and as being of unlimited size. “[A]n idealization can be radically untrue but nonetheless facilitate understanding. The divergence from truth can contribute to representing a pattern embodied by the focal phenomenon but from which the phenomenon deviates to some degree – perhaps even a large degree” (Potochnik Reference Potochnik2017: 100).
Game theoretic models thus function in very different ways than their target systems, and are imperfectly faithful in representing them, but still make significant understanding more likely.
The idealizations in LIME models work to confer this benefit, also. In order to achieve understanding why a decision was made, stakeholders need to grasp an explanation that contains causal pattern information. These patterns must be selected from an enormous plethora of causal patterns which are true of the target phenomena, but which are not the causal patterns of interest to the stakeholders. DNNs (and other black box models) contain a huge number of causal regularities. Some involve higher-level features that aren't comprehensible; others involve the internal workings of each unit in a DNN, which may also be unintelligible to lay people, and in any case aren't very illuminating. Neither of these kinds of causal patterns are relevant. What the stakeholder wants are the kind of causal patterns that will allow them to understand which factors led to their decision, how things might have gone differently if those factors had been different, and how to receive a different result next time (i.e., how to obtain recourse) (Venkatasubramanian and Alfano Reference Venkatasubramanian and Alfano2020; Vredenburgh Reference Vredenburgh2022). LIME produces explanations that include information about these more relevant causal patterns. It does so by idealizing away the influence of factors which are genuine difference-makers, but which don't figure in the causal patterns of interest, and which might confound ability to recognize the relevant causal patterns.
LIME's locality is one aspect that allows for this focusing. Recall that LIME works by perturbing or slightly changing the actual input to the original model to see what effect that would have on the original model's output. It figures out which features can be changed in a small way, so that there is a significant difference to the output. It then highlights these features as important, and sets aside the other features. However, LIME is paying attention to individuals that are similar to the original input, where similarity is a matter of how small the changes are from the original input. The features LIME treats as unimportant are only unimportant in the local region – i.e., for individuals whose features are similar to the original individuals. If the unimportant features were changed drastically enough, the resulting individual would not be similar enough to count as in the local region. Hence, LIME ignores such large changes to a feature.
So, the idealization in question here is that certain features are represented as if they weren't important at all, when in fact they could be: if those features were changed significantly enough, they could change the output. But LIME's purpose is to give useful explanations that can help inform and guide stakeholders. This is facilitated by focusing on minor changes to features, because minor changes are the ones more likely to be made, and are more plausible when given as action guidance for individuals. For instance, in explaining a loan application system, it would be more useful for individual loan applicants to know that a small change in income will effect whether they get a loan, rather than an enormous change to the size and number of loans they have already taken. In other words, it is the interests of the stakeholders (the developers, deployers, and decision-subjects) of the system that makes LIME's focus on small changes useful.
Thus, LIME has the third beneficial feature (and sign) of idealization. It focuses attention on specific causal patterns. It is thereby relevantly similar to idealized models such as those used in evolutionary game theory.
7.4. Rejecting P3
Thus, the very features of LIME models which make conjuncts (a) and (b) of P3 true, can in fact make it more probable that stakeholders achieve a high-degree of understanding. The difference in the computed function, and the lack of faithfulness, are misrepresentations that serve as idealizations. This gives us strong reason to reject P3. And so, the rationalization objection fails. There is no in-principle reason to think that XAI methods provide us only ersatz-understanding, or provide too weak an understanding to be adequate for the purposes XAI is employed for.
7.5. Lingering Skeptical Worries
There is one final set of worries worth addressing immediately. One might still have lingering doubt that we should take XAI methods to produce models that genuinely represent their targets. That is, even if the rationalization objection as I have rendered it fails, the initial intuitive worry remains: XAI methods misrepresent their target black box models in at least some ways, and they seem to operate in totally different way than these models. Moreover, we don't fully understand how the original models work, ex hypothesi. So how can we be sure that what the XAI models tell us about the original model is true? How can we be sure that we are being offered genuine causal models, rather than just-so stories?Footnote 19
In response, I think we should recognize that we are in roughly the same position with respect to scientific models quite generally. Scientific models are used to understand complex phenomena that we have no other way of understanding. We have no way of knowing and understanding mechanisms of bat evolution, subatomic particle interaction, or climate change, except via our models. And these models are not perfectly accurate (or faithful) representations of their target phenomena, either. The reasons we have to trust those models concern their empirical adequacy, predictive power, explanatory power, and theoretical virtues (Downes Reference Downes2020; Frigg and Hartmann Reference Frigg and Hartmann2020). The idealized models produced by XAI methods should be judged by the same standards, and insofar as they are well-supported models, we should think they can provide significant understanding.
Admittedly, there are reasons to worry that XAI methods are not currently producing well-supported models in many of their use cases. In particular, recent work has shown that different XAI methods often appear to disagree with each other (Krishna et al. Reference Krishna, Han, Gu, Pombra, Jabbari, Wu and Lakkaraju2022). For instance, LIME and SHAP might suggest that different features are the most important to explaining the same classification made by an opaque AI system. A similar problem is that some XAI methods lack robustness in the face of adversarial attacks (Slack et al. Reference Slack, Hilgard, Jia, Singh and Lakkaraju2020).
However, XAI research is new, and the techniques currently being applied are just the beginning of that research. So, successful uses of XAI methods may (or may not) be relatively rare at the moment. My main point here is that there is no in-principle reason to halt that research on the grounds that it is fundamentally misguided and can only hope to offer us “ersatz understanding”, as many critics allege. Moreover, the understanding account, combined with the “models-of-models” view of XAI methods, offers the promise of useful guidance in future XAI research, particularly concerning the disagreement problem. Philosophy of science has a wealth of conceptual resources for thinking about confirmation, model justification, disagreement, and underdetermination. This is an avenue I intend to pursue in future work.
8. Conclusion
The understanding-account of TIE and opacity alleviation thus offers a significant theoretical benefit: it helps vindicate and make sense of the use of explainable AI models. This offers at least some support to the framework. Moreover, using understanding and communicative explanation as fundamental notions allows a coherent framework that eliminates the conceptual confusion in TIE research that has often been complained about. Establishing the truth of this understanding-based framework may require additional support. But the arguments offered here provide strong reason for continued inquiry on the basis of this account.Footnote 20






