2. Convex hulls of evaluations and nonclassical probability

The project of axiomatizing convex hulls of nonclassical evaluations has its ultimate goal in describing credence functions which would be rational in nonclassical settings. Let us postpone the discussions of rationality to section 4 and focus now on the aforementioned convex hulls.

We shall begin by stating Paris’ initial result in the framework introduced in the recent handbook article by Williams (Reference Williams, Hájek and Hitchcock2016). It requires a finite propositional language ${\cal L}$ with the set of sentences $Sent_{\cal L}$ built using a set of connectives which includes ∨ and ${\wedge} $ (but possibly also other ones, including modalities). ${\opf V}$ is a certain subset of the set of all functions from $Sent_{\cal L}$ into a finite nonempty set of truth values TV. Williams introduces the term “cognitive load”:Footnote ⁴ a cognitive load of a truth value is the supposed “ideal cognitive state” associated with it; in other words, it is the degree of belief an omniscient agent should invest in a proposition having that truth value. In the classical case, cognitive loads directly correspond to truth values 1 (true) and 0 (false), while in the general case the cognitive load function c is an arbitrary function from TV into [0, 1]. For any valuation V we can speak of “its” cognitive evaluation $c_V\colon \ Sent_{\cal L}\to [ {0, \;1} ] $ defined as, for any $\varphi \in Sent_{\cal L}$, c _V(φ) = c(V(φ)). Williams's idea is, in the context of some logic, to inquire about the convex combinations of something else than valuations. The reason for this is that two different logics, defined on the same language and having the same set TV of truth values, may give rise to exactly the same set of valuations. And yet, for example due to how the consequence relation differs between the two logics, the epistemic status of these valuations might be different.

Let us note that according to both Williams and Bradley the logics themselves are “cognitively loaded”, in that each truth value has “its” cognitive load (Williams Reference Williams, Hájek and Hitchcock2016: 255).Footnote ⁵ For the purposes of stating the formal results we can therefore treat the cognitive load function to be a definitional element of the given logic. The logics are also “semantically driven”; we have our doubts as to what exactly this means,Footnote ⁶ but at the very least it seems to entail:

• • first, that a logic expressed in a language carries with itself the information about what the possible valuations of the sentences of that language are (i.e. if a logic is semantically driven, it's not something for which we could find different semantics: if you change the semantics, you change the logic);

• • second, that truth values are categorical properties of sentences (as opposed to, say, uninterpreted formal devices used in achieving a different goal; see Field Reference Field2009);

• • third, that the logic involves a consequence relation defined so that whether a sentence entails another depends only on facts regarding valuations (and not, for example, on any syntactic considerations).

Before we state the starting result, let us note that we have made a conscious decision to depart from Paris’ original assumptions, to the effect that all languages under consideration here will include only truthfunctional operators. This is just for reasons of presentation. The main system under discussion, the Symmetric Logic, only includes operators of this kind anyway. But nonetheless, doing so allows us to simplify some statements of theorems based on Paris’ results. The languages in question have finitely many propositional variables and operators and the logics admit only finitely many possible valuations. Thanks to this we can speak of the function “B”Footnote ⁷ as opposed to “every finite restriction of B” being a convex combination of some vectors. More complicated variants of the relevant results, taking into account also non-truthfunctional operators, can be provided after the inspection of Paris (Reference Paris2005).

Without further ado, here's the generalized version of Paris’ theorem.

1. (*) the image of c is {0, 1};

2. (**) ∨ and ${\wedge} $ operate classically with respect to the cognitive loads; that is, for any cognitive evaluation c _V,

   $$c_V( {\varphi \vee \psi } ) = 0{\rm \;iff\;}c_V( \varphi ) = c_V( \psi ) = 0$$
   and
   $$c_V( {\varphi \wedge \psi } ) = 1{\rm \;iff\;}c_V( \varphi ) = c_V( \psi ) = 1; \;$$

3. (***) the consequence operation satisfies the ‘no drop’ condition on the cognitive evaluations, that is,

   $$\varphi \,{\rm \models }\,\psi {\rm \;iff\;for\;any\;valuation\;}V{\rm , \;\;}c_V( \varphi ) \le c_V( \psi ) ; \;$$

then the following are equivalent.

1. (A) B is a convex combination of the cognitive evaluations from ${ c_V \vert V\in {\rm {\opf V}}} $;

2. (B) B satisfies the axioms below.

   • (${\cal L}$1) If ${\rm \models }\varphi $ then B(φ) = 1, and if $\varphi \,{\rm \models }$ then B(φ) = 0,

   • (${\cal L}$2) If $\varphi \,{\rm \models }\psi $ then B(φ) ≤ B(ψ),

   • (${\cal L}$3) $B( {\varphi \vee \psi } ) + B( {\varphi \wedge \psi } ) = B( \varphi ) + B( \psi ). \hskip 10.6pc$■

Already in three-valued cases the situation becomes non-trivial. If the set of truth values is, say, {T, O, F} (for “true”, “other”, and “false”), the ideal cognitive state associated with O can be one of a number of things. If, for example, the logic dictates that O be read as “half-true”, then the cognitive load of O can be naturally taken to be ½. (This will be the main case under discussion in the current paper.) For other logics, as we will see below, the ideal degree of belief invested in a proposition which has the truth value O might be 0 (if believing such a proposition should, according to the logic, be avoided), or 1 (if it is as belief-worthy as a true proposition). And, correspondingly, what rational credences are should depend on which logic governs the possible worlds: even if the set of valuations may be exactly the same.Footnote ⁹

If we use the term “L-probabilities” for the elements of the convex hull of L's cognitive evaluations, Theorem 2.1 says in effect that if L satisfies (*)-(***), then L -probabilities are axiomatized by (${\cal L}1$)–(${\cal L}3$). The general problem is to give axiomatizations of M -probabilities for logics M which do not satisfy at least one of the conditions (*)–(***), and we will consider here a particular case in which it is just the condition (*) that is violated: that is, the logic in question admits more than two cognitive loads.

A straightforward application of (a version of) Theorem 2.1 is noted by Williams in the context of the well-known three-valued logics KL (Kleene's “strong logic of indeterminacy”) and LP (Priest's “logic of paradox”). In fact, the Strong Kleene truth-tables used by them serve as the basis of probably the least complicated examples of the issue under discussion.Footnote ¹⁰ The three-valued logics KL and LP along with the Kleene truth tables are introduced and discussed in detail in section 7.3 of Priest (Reference Paris2001).

Consider, then, a sentential language ${\cal L}$ consisting of a non-empty finite set P of propositional variables and the three connectives ${\wedge} $, ∨ and ¬. A valuation V assigns to each propositional variable one of the three possible truth values: T, O, and F. It is then extended to a mapping $V\colon \ Sent_{\cal L}\to { {T, \;O, \;F} } $ by the rules given by the Kleene truth tables as follows:

$$\hskip -5pc\matrix{\wedge &T &O &F\cr T &T &O &F \cr O & O &O &F\cr F &F &F &F}\hskip -4pc \vrule \hskip 4pc \vskip 1pt \hskip 2pc\matrix{\quad \unicode{x2228} &T &O &F\cr \quad T &T &T &T\cr \quad O &T &O &O\cr \quad F &T &O &F}\hskip -4pc\vrule \hskip 6pc \vskip 1pt\matrix{\unicode{x00AC} &T &O &F\cr &F &O &T}\hskip -4pc \vskip -1pc\vrule height 1pt $$

The logics KL, LP and the “Symmetric Logic” SL use these truth tables; however, they differ in how their consequence relation ${\rm \models }$ is defined:

KL: $\varphi \,{\rm \models }_{\,KL}\,\psi $ iff for every evaluation V we have

(1)$${\rm if\;}V( \varphi ) = T, \;\;{\rm \;then\;}V( \psi ) = T.$$

LP: $\varphi \,{\rm \models }_{\,LP}\,\psi $ iff for every evaluation V we have

(2)$${\rm if\;}V( \varphi ) = T{\rm \;or\;}O, \;\;{\rm \;then\;}V( \psi ) = T{\rm \;or\;}O.$$

SL: $\varphi \,{\rm \models }_{\,SL}\,\psi $ iff for every evaluation V we have

(3)$${\rm if\;}V( \varphi ) = T, \;\;\;{\rm then\;}V( \psi ) = T; \;{\rm \;and}$$

(4)$${\rm if\;}V( \varphi ) = O, \;\;\;{\rm \;then\;}V( \psi ) = T{\rm \;or\;}O.$$

That is, ${\rm \models }_{SL}$ is ${\rm \models }_{KL}$ and ${\rm \models }_{LP}$ “taken together”: $\varphi \,{\rm \models }_{\,SL}\,\psi $ iff ($\varphi \,{\rm \models }_{\,KL}\,\psi $ and $\varphi \,{\rm \models }_{\,LP}\,\psi $). KL has no tautologies, a fortiori the principle of excluded middle φ∨¬φ also fails to be one. LP is a paraconsistent logic, where $\varphi \wedge \neg \varphi $ is not explosive, i.e., it does not entail everything. SL allows us to enjoy both of these features.

In the 2016 handbook article Williams claims that the following are the cognitive loads of the three logics:

Note that, indeed, if we grant this assumption, then the logics KL and LP satisfy the conditions (*)–(***) and thus Theorem 2.1 can be applied to them directly.Footnote ¹¹ Williams notes further that “it is a matter of hard graft to see whether similar completeness results can be derived for settings that fail the Parisian conditions (one representative of which is our Symmetric logic)”. As already mentioned, Paris himself extends the result so that it applies to finitely-valued Łukasiewicz logics, while Mundici (Reference Mundici2006) achieves a similar goal for the infinitely-valued version.Footnote ¹² Bradley (Reference Bradley2017) continues the “hard graft”, covering some examples involving languages with non-truthfunctional operators.Footnote ¹³ Our main goal here is to investigate how such nonclassical axioms can be argued to be requirements of rationality using Dutch Book considerations, an idea frequently mentioned, but one that has not, it seems, been so far put under sufficient scrutiny. Our point of departure will be the relatively uncomplicated example of Symmetric Logic, to which we now turn.

3. Axiomatizing convex hulls of Symmetric Logic

We have recently put forward the following solution of the problem of axiomatizing SL-probabilities in Gil Sanchez et al. (Reference Sanchez M., Gyenis and Wroński2022):

1. (A) B is a convex combination of the cognitive evaluations $c_V^{SL} $ for V ∈ ${\opf V}$.

2. (B) B satisfies the axioms below.

   1. (SL1) If $\varphi \,{\rm \models }\,\psi $ then B(φ) ≤ B(ψ),

   2. (SL2) B(¬φ) = 1 − B(φ),

   3. (SL3) $B( {\varphi \vee \psi } ) = B( \varphi ) + B( \psi ) -B( {\varphi \wedge \psi } ) $,

   4. (SL4) $B( \varphi ) = B( {\psi \wedge \varphi } ) + B( {\neg \psi \wedge \varphi } ) -B( {\varphi \wedge \neg \varphi \wedge \psi \wedge \neg \psi } ). \hskip 4.6pc $■

In other words, SL-probabilities are axiomatized by the conditions (SL1)–(SL4).Footnote ¹⁴

For an extended proof of this Theorem, see Gil Sanchez et al. (Reference Sanchez M., Gyenis and Wroński2022). One aspect of SL we've made use of is that, of the three logics KL, LP and SL, it is only the Symmetric Logic that is algebraizable: that is, only in that case the relation of mutual entailment is a congruence, and so the logic has its Lindenbaum–Tarski algebra.Footnote ¹⁵ (Also, for similar reasons as in the classical propositional logic case above, the condition that P is finite cannot be dropped without significant modifications. The papers by Paris (Reference Paris2005) and Williams (Reference Williams2012b) contain an exhaustive list of similar results for other logics and the issue of compositionality is also discussed therein.)

Notice that if the language has just a single propositional variable, all credences satisfying (SL1)–(SL4) are convex combinations of the three valuations displayed in Figure 1; that is, they are credences of this form:

Figure 1. The leftmost picture displays the Lindenbaum–Tarski algebra of the single-variable version of SL. The others display the three valuations possible in this context.

The following is an example of such a credence:

It is important to distinguish two goals: the logical one of axiomatizing certain convex hulls, and the epistemological one of arguing that credences satisfying those axioms, or, equivalently, belonging to those convex hulls, are in some sense rational. With regard to the cognitive evaluations of Symmetric Logic, we've just described the achievement of the first of those two goals. We now turn to the second one.Footnote ¹⁶

4. Convex hulls, Dutch Books and rationality

It is one thing to axiomatize the notion of a convex hull of cognitive loads in the context of some logic. It is another one to argue that these axioms should be satisfied by rational credence functions; in fact, it is achieving this goal that for epistemologists is probably the main allure of these considerations. Let us now turn to this task.

The chief reason stated in Paris (Reference Paris2005) for investigating axiomatizations of convex hulls of sets of valuations was that it is exactly the elements of such convex hulls that are not Dutch-bookable with respect to those valuations.Footnote ¹⁷ One assumption was that the valuations are {1, 0}-valued; however, Paris himself noted that this restriction could “clearly be relaxed”. Section 3 of Williams (Reference Williams2012a) contains a somewhat informal proof of a generalization of Paris’ result to finite “non-classical truth value distributions of truth values”.Footnote ¹⁸ Once cognitive loads are introduced, matters become a little bit more subtle. Assume possible worlds are governed by a logic with three truth values: True, Other, and False. Suppose a bet is bought for a proposition A with the stake S; and that it turns out that the truth value of A is Other. What portion of S should be paid out – what Williams (Reference Williams, Hájek and Hitchcock2016) calls the “pragmatic load” of the Other value – depends on how Other is to be interpreted; it can be argued, e.g., that if the logic is KL, then the buyer should get nothing, if it is the LP, (s)he should receive the full S, and if it is the SL, then (s)he should end up with one half of S. In section 5 of the 2016 paper Williams points out that the demands belong to the convex hull of cognitive evaluations and don't be Dutch-bookable might be inconsistent if cognitive loads differ from the pragmatic ones. To discuss the Paris-motivated connection between Dutch Books and convex hulls we thus assume that these two types of loads coincide.

Some comment regarding cognitive and pragmatic loads is in order. Williams (Reference Williams, Hájek and Hitchcock2016) takes them, in the context of some logic, to be properties of truth values.Footnote ¹⁹ This allows a hypothetical situation in which two different truth values share their cognitive load (say, 1) but differ in their pragmatic load (say, 1 vs. ½). In such a case, even though there is no difference in the credence an omniscient agent should invest in a proposition depending on which of the two truth values it has, one of them is “worth more” in a betting situation. Similarly, truth values with differing cognitive loads might share their pragmatic load. One could certainly contemplate a different approach, in which one of the two types of loads was fundamental to the other; for example, pragmatic loads could be taken to “generate” cognitive loads, on the assumption that what omniscient agents care about can be reduced to betting profits. Since our project is to begin investigating how Dutch Books could be made to actually work in nonclassical settings, we shall put these issues aside here; matters will already be nontrivial if we stick to the identification of cognitive loads and pragmatic loads for the time being. And so, even if we will eventually argue that in nonclassical contexts the notion of Dutch Book needs to be modified, we shall now state the following generalization of Paris’ result using just the cognitive loads.

Assume, again, that we are given a propositional language ${\cal L}$ with finitely many propositional variables and finitely many operators which include ∨ and ${\wedge} $.

4.1 definition (dutch book). In the context of a logic with the set of valuations ${\opf V}$, and the set of cognitive evaluations {c _V|V ∈ ${\opf V}$}, a function $B\colon \ Sent_{\cal L}\to [ {0, \;1} ] $ permits a Dutch Book iff there are $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$ and s ₁, …, s _n ∈ ℝ such that for all elements of {c _V|V ∈ ${\opf V}$} we have

(5)$$\mathop \sum \limits_{i = 1}^n s_i( c_V( {\vartheta_i} ) -B( {\vartheta_i} ) ) < 0.$$

The shape of Formula (5) should be familiar to any reader of formal epistemology. The usual interpretation of the terms involved is as follows (assume, for brevity, that you can read “B” as “an agent with the credence function B” whenever you feel it would be natural):

• • s _i – the prize (stake) associated with the bet for $\vartheta _i$;

• • $s_i\cdot B( {\vartheta_i} ) $ – the cost of that bet;Footnote ²⁰

• • $s_i\cdot c_V( {\vartheta_i} ) $ – the payout if $\vartheta _i$ has the truth value $V( {\vartheta_i} ) $;Footnote ²¹

and, crucially, it is understood that according to B, $s_i\cdot B( {\vartheta_i} ) $ is the fair price for a bet with such a payout.Footnote ²² A Dutch Book against B, then, is a collection of bets all of which B considers to be fairly priced but which taken together inevitably lead to loss.

Dutch Books are to be a sign of irrationality. Assume, then, that possible worlds are governed by the Symmetric Logic; for simplicity, suppose the language only has two variables, x and y. What's wrong with not satisfying the (SL1)–(SL4) axioms? Since the first three conditions have been widely discussed in the literature,Footnote ²³ let us consider a B which violates (SL4) and construct a Dutch Book against it.

For convenience, let us label the sentence $x\wedge \neg x\wedge y\wedge \neg y$ – whose cell of the Lindenbaum–Tarski algebra for our logic is its bottom element – as ⊥. Consider a B such that $B( x ) = 1{\rm /}3, \;B( {y\wedge x} ) = B( {\neg y\wedge x} ) = 1{\rm /}4$ and B(⊥) = 1/12. Note that it does not follow from this assignment that any of the first three SL axioms be violated; however, (SL4) fails, since

$$1{\rm /}3 = B( x ) < B( {y\wedge x} ) + B( {\neg y\wedge x} ) -B( \bot ) = 5{\rm /}12.$$

To create a Dutch Book against this B we set the values for use in Formula (5) as per Table 1. Those values, according to the interpretation given above, mean that B considers it fair to:

• • sell the bet for x for 4;

• • sell the bet for ⊥ for 1;

• • buy the bet for $y\wedge x$ for 3;

• • buy the bet for $\neg y\wedge x$ for 3.

Table 1. The values for use in Formula (5), to create a Dutch Book against the B defined in the text.

Should all these bets go through, B would suffer a prior loss: −1. The payouts from the bets in various worlds are given in Table 2. As we can see, the whole situation is a Dutch Book against B: no matter what happens, B ends up losing 1.

Table 2. The payout table for the bets against a B violating the axiom (SL4) as discussed in the text.

However, we find it highly doubtful that the existence of this Dutch Book is a sign of B's irrationality. Bluntly put, why should B even care about this particular sets of bets? Why should we stipulate that the values from Table 1 encode numbers which B would take to be fair prices for the corresponding bets? For example, B(x) = 1/3. Why would B consider it to be fair to sell the bet for x – which pays 12 if the cognitive load of x is 1, pays 6 if it is 1/2, and pays 0 otherwise – at the price of 4, that is, at one-third of the highest possible prize?

This assumption, which lies at the foundation of applying the Dutch Book idea in nonclassical settings, seems not to have received sufficient scrutiny in the relevant literature. Williams (Reference Williams2012a: 817) writes “[a]s is standard in Dutch Book arguments, we assume that the fair price for an individual bet with unit prize for an individual with belief state b is specified by the degree of belief that b assigns to the proposition bet upon”. He continues that he's “not interested in whether the argument works”, and would rather investigate the “geometric structure of the argument”. However, from an epistemological point of view, in order to transform the formal insights into some conclusions regarding norms of rationality, we should definitely be interested whether the argument works. And on the most prevalent, indeed canonical, way of cashing out the notion of “fair price”, it just does not work.

The most common way of thinking about “fair price” in Dutch Book contexts, recall,Footnote ²⁴ is to use the notion of expected value, and to think of bets which are fair according to B as those which B expects to favour neither buyer nor seller; that is, those which according to B have the expected value 0. Classically, to calculate the expected value of a bet for A from the perspective of B, we use the credence in that A is true, that is, B(A), and the credence in that A is false, which we equate with B(¬A).Footnote ²⁵ Since these alternatives exhaust the available options, we can calculate B's expected profit from the given bet, assuming the price and the prize are provided. However, it should be clear that already in a three-valued setting this approach will not work. If the payout – whether ‘cognitive loads’ are considered or not – depends on the truth value of A, then we are lacking the required information about the credence in that A obtains the ‘third’ truth value. The values of B for A and ¬A, even assuming that the latter denotes the degree of belief in that A is false, are simply not enough to calculate B's expected profit from the bet.

We will now propose a fix thanks to which we can, in nonclassical settings, consider Dutch Book arguments that indeed work.Footnote ²⁶ It involves a modification of the usual notion of credence. On our proposal it will assign to propositions not single numbers, but rather vectors of numbers: as many as there are truth values according to the logic which governs the space of possible worlds. The approach will be similar to the one used in Janda (Reference Janda2016) in the context of accuracy measures. It will turn out that some results obtained using the usual notion of credence – for example, the axiomatization of the convex hulls of evaluations of SL – can be transformed so that their variants hold also when the new notion is used.

4.1 Credences as Complex Attitudes

The idea is to treat credence in a proposition as a complex attitude, with as many dimensions as there are truth values. If, say, propositions can be True, False, or Half-True, one's credence in A is a triple of numbers: degrees of belief in that A is True, in that A is False, and in that A is Half-True.

More generally, assume a logic L is given in a language ${\cal L}$ with valuations assigning to sentences elements from a finite set of truth values TV.Footnote ²⁷ In such a context, credences are functions $B\colon \ TV \times Sent_{\cal L}\to [ {0, \;1} ] $. We will use the expression $B_\ast ( A ) $ to denote B(*, A); it is to be read as “credence in that A has the truth value *”. If there are n truth values, we could equivalently be talking either about B or about n functions from $Sent_{\cal L}$ to [0, 1]; for example, in the case where TV has three elements – whatever they are – it might be convenient to speak about a credence function by referring to the indexed set of functions {B ₁(⋅), B _1/2(⋅), B ₀(⋅)}.Footnote ²⁸

While the ideas here are meant to be general, so that a variety of nonclassical logics and corresponding notions of credence can be considered, all examples illustrating our points will be given using the Symmetric Logic. As the Reader is well aware, it has three truth values, and three cognitive loads; while we noted that, under the assumptions that pragmatic loads are identical to cognitive loads, it is the cognitive loads which determine payouts from bets, in this particular case we can assume without loss of generality that it is the truth values that are doing the job. We will thus dispense with the notion of cognitive loads for the time being (we will come back to it in the general Definition 4.5). Let us also think of valuations as possible worlds, not because we wish to put any deep philosophy behind this choice, but so that we can conveniently speak of propositions having a certain truth value “at” a valuation V, and of agents “having profits” or “sustaining losses” at various V's.

For convenience we assume that for any proposition all credences in that proposition having one of the various truth values sum up to 1; nothing formally important hangs on that, but without this assumption some formulas below would have to be more complicated. The idea is that there's some quantity of credence that's distributed among the possible options (the proposition in question having the various truth values); the convenient assumption amounts to a normalization of that quantity. We will write it out explicitly, since it does give us a philosophical bonus at one point, which some might find to be debatable:

Convenient Assumption (CA). For any $A\in Sent_{\cal L}$, $\sum _{{\ast}{\in} TV}B_\ast ( A ) = 1$.

Let us see how we can connect our modified concept of credence with the notion of bet assumed in Definition 4.1 and Theorem 4.2 to obtain examples of Dutch Book arguments in non-classical settings which actually work.

Following, for now, the lead of Williams (Reference Williams2012a), let us generalize the idea that a bet for A with the prize S pays out S if A is true and nothing if A is false. In other words, a bet for A pays out the portion of S given by the truth value of A.Footnote ²⁹ That is, for a valuation V, a bet for A with the prize S pays out V(A) ⋅ S at V. For an agent who buys such a bet at cost C, then, the profit in V is w(A) ⋅ S − C. We're after capturing the essence of Dutch-bookability, that is exploitability via fair bets: a Dutch Book against an agent (a credence function) is a collection of fair bets (that is, bets which are fair according to the agent's credence function) which ultimately lead to inevitable loss on part of any agent which would partake in all of them.

Which bets does a credence function consider fair? Given a proposition and a prize, a fair bet is that which has a fair price. We have already mentioned that, especially non nonclassical contexts, the formal epistemology literature has largely avoided extensive commentary on this issue. Typically, a price is considered to be fair according to B if under that price B expects the bet to favour neither buyer nor seller: according to B, the bet has the expected value 0.Footnote ³⁰

Let us try to formulate a definition of a Dutch Book, suitable for nonclassical contexts, based on this notion of a fair price. How to cash it out formally? In our opinion the following idea is natural: given a prize S and proposition A, the expected value of a bet for A which costs C according to the credence function $B = { {B_\ast } } _{{\ast}{\in} TV}$ is

$$\mathop \sum \limits_{{\ast}{\in} TV} B_\ast ( A ) ( {\ast{\cdot} S-C} ) .$$

We're not the first to use the word ‘expected’ in this way: what we're doing here is essentially the same thing as e.g. what is proposed in section 2 of Leitgeb and Pettigrew (Reference Leitgeb and Pettigrew2010), where the authors define ‘expected inaccuracy’, with the expectation calculated from the perspective of functions which are not assumed to be probabilities.Footnote ³¹ (Our $B_\ast ( A ) $'s sum up to 1 for each A, so the formula looks like the classical expected value, but this is just because of our Convenient Assumption, made only for the purpose of simplifying the formulas involved.)

As already mentioned, we will be using SL to illustrate the proposed ideas. Assume, then, that the set of truth values is TV = {1, 1/2, 0}, and that a bet for A with prize S pays out * ⋅ S where * is A's truth value. It is then immediate to note that if B(⋅) = {B ₁(⋅), B _1/2(⋅), B ₀(⋅)}, then B's fair price for a bet for A with prize S is (B ₁(A) + 0.5 ⋅ B _1/2(A)) ⋅ S.Footnote ³² We can thus now put forward the following definition of what it means for a credence to be Dutch-bookable, assuming it is the Symmetric Logic that governs the possible worlds.

4.3 definition (SL -really-dutch-bookable). B = {B ₁(⋅), B _1/2(⋅), B ₀(⋅)} is SL -really-Dutch-bookable if there are $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$ and s ₁, …, s _n ∈ ℝ such that for all v ∈ ${\opf V}$ we have

(6)$$\mathop \sum \limits_{i = 1}^n s_i( V( {\vartheta_i} ) -( B_1( {\vartheta_i} ) + 0.5\cdot B_{1{\rm /}2}( {\vartheta_i} ) ) ) < 0.$$

That is, assuming that SL governs the possible worlds, B is really-Dutch-bookable if there is a series of bets B considers to be fair which inevitably lead to B's loss: and thus the main intuition behind the notion of a Dutch Book is indeed captured.

It turns out we can use the result reported earlier, the axiomatization of convex hulls of evaluations of SL logic, to precisely specify which credences are not SL-really-Dutch-bookable:

4.4 Fact. {B ₁(⋅), B _1/2(⋅), B ₀(⋅)} is not SL-really-Dutch-bookable iff $B_1({\cdot} ) + 0.5\cdot B_{1{\rm /}2}({\cdot} ) \colon \ Sent_{\cal L}\to [ {0, \;1} ] $ satisfies (SL1)–(SL4).

Proof. Define an ‘old-style’ credence function $b\colon \ Sent_{\cal L}\to [ {0, \;1} ] $ as follows: b(φ): = B ₁(φ) + 0.5 ⋅ B _1/2(φ). Then proceed through the following equivalences: B ₁(⋅) + 0.5 ⋅ B _1/2(⋅) satisfies (SL1)–(SL4) iff b satisfies (SL1)–(SL4) iff b is not Dutch-bookable (in the sense of Definition 4.1, due to Theorem 4.2) iff there are no $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$ and s ₁, …, s _n ∈ ℝ such that for all V ∈ ${\opf V}$ (5) is satisfied (with b in place of B) iff there are no $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$ and s ₁, …, s _n ∈ ℝ such that for all V ∈ ${\opf V}$ (6) is satisfied iff {B ₁(⋅), B _1/2(⋅), B ₀(⋅)} is not SL-really-Dutch-bookable. ■

We thus have an example of a nonclassical setting and a Dutch Book argument that actually works in it: a function B = {B ₁(⋅), B _1/2(⋅), B ₀(⋅)} is not susceptible to an SL-real-Dutch Book only if B ₁(⋅) + 0.5⋅B _1/2(⋅) satisfies (SL1)–(SL4); otherwise there is a set of bets B considers to be fair which inevitably leads to B's loss.

By way of illustration, let us see an example of a real Dutch Book in the SL setting. We will recreate the previous example in the new, ‘complex’ setting. Consider a credence {B ₁, B _1/2, B ₀} with the values as given in Table 3. It is routine to check that (CA) is satisfied and that

$$\matrix{ {1{\rm /}3 = B_1( x ) + 0.5\cdot B_{1{\rm /}2}( x ) < B_1( {y\wedge x} ) + 0.5\cdot B_{1{\rm /}2}( {y\wedge x} ) + B_1( {\neg y\wedge x} ) \,+ } \cr { + 0.5\cdot B_{1{\rm /}2}( {\neg y\wedge x} ) -B_1( \bot ) -0.5\cdot B_{1{\rm /}2}( \bot ) = 5{\rm /}12, \;} \cr } $$

that is, B ₁ + 0.5⋅B _1/2 does not satisfy (SL4). The Dutch Book presented before shows that {B ₁, B _1/2, B ₀} is really-Dutch-bookable; in Table 1 it suffices to substitute $B_1( {\vartheta_i} ) + 0.5\cdot B_{1{\rm /}2}( {\vartheta_i} ) $ for $B( {\vartheta_i} ) $.

Table 3. A ‘complex’ credence function such that B ₁(⋅) + 0.5⋅B _1/2(⋅) gives the values of the credence function defined in Table 1, against which a Dutch Book exists as evidenced by Table 2.

Having illustrated the idea behind real Dutch-bookability in the case of SL, let us give the general definition, involving cognitive loads (but sticking with the assumption that they are to be identified with pragmatic loads and continuing to assume (CA)). Suppose, then, that a logic L is given in a language ${\cal L}$ as $( {{\rm {\opf V}}, \;{\rm \models }, \;c} ) $ with the valuations obtaining values in a finite set TV. Suppose that for each * ∈ TV, c(*) ∈ [0, 1]. If L is to be considered as governing the possible worlds, then credence functions B should be considered as being of the form $B = { {B_\ast ({\cdot} ) } } _{{\ast}{\in} TV}$. Then B's expected profit from a bet for A which costs C and pays off c(V(A))⋅S at world V is

(7)$$\mathop \sum \limits_{{\ast}{\in} TV} B_\ast ( A ) ( c({\ast} ) \cdot S-C) .$$

The fair price of such a bet from the perspective of such a B is the unique C which makes the expression (7) equal 0, that is, $C = \sum _{{\ast}{\in} TV}B_\ast ( A ) \cdot c({\ast} ) \cdot S$. (Note that this does indeed give back the classical “the fair price is the proportion of the prize which corresponds to the degree of belief” idea once enough assumptions are in place.)

With this in hand we can formulate the following general definition.

4.5 definition (L-really-dutch-bookable). Suppose a logic L is given in a language ${\cal L}$ as $( {{\rm {\opf V}}, \;{\rm \models }, \;c} ) $ with the valuations obtaining values in a finite set TV. Suppose that for each * ∈ TV, c(*) ∈ [0, 1], and that credence functions B are of the form $B = { {B_\ast ({\cdot} ) } } _{{\ast}{\in} TV}$.

B is L-really-Dutch-bookable if there are $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$ and s ₁, …, s _n ∈ ℝ such that for all v ∈ ${\opf V}$ we have

$$\mathop \sum \limits_{i = 1}^n s_i\Big( c( {V( {\vartheta_i} ) } ) -\mathop \sum \limits_{{\ast}{\in} TV} B_\ast ( {\vartheta_i} ) \cdot c({\ast} ) \Big) < 0.$$

Note that if L is the classical logic, with $TV = { {True, \;False} } $ and c(True) = 1, c(False) = 0, then the above gives us the ‘typical’ notion of a Dutch Book. For a credence function B = {B ₁(⋅), B ₀(⋅)}, the expected value of a bet for A which costs C and whose prize is S is equal to B ₁(A)⋅(S − C) − B ₀(A)⋅C (so, just like it should be, credence in ¬A is not involved) and a variant of the norm of Probabilism can be recovered.

We hope L-real-Dutch-bookability will be studied for various logics L and that it will be possible to establish more connections between this notion and axiomatizations of sets of the given logic's cognitive evaluations – an example of which is our Fact 4.4.

In the future it might also be fruitful to consider ‘complex’ cognitive loads. We've already mentioned our uneasiness with Williams’ proposal that in the case of LP the cognitive load of the truth value Other should be set to 1 just because its intended interpretation is “is both true and false”. Perhaps a more natural reading would be to say that, assuming LP, the credence an omniscient agent should assign to a proposition A with the truth value Other is {B ₁(A) = 1, B _1/2(A) = 0, B ₀(A) = 1}. We leave this topic for future research.

In most discussions of credential norms we find in formal epistemology, we can point to three aspects which are in a sense ‘classical’: the credence functions (considered as assigning single numbers to propositions), the (sometimes implicitly) classically conceived semantics, and the notion of a bet which is usually used in the literature. This paper contributes to the discussion in which the starting assumption is that the second element should be varied: the semantics under consideration may be nonclassical. In this section we have so far been discussing varying the first element, so that we end up using some nonclassical version of the credence notion. However, one might not be happy with us keeping the notion of a bet as employed by Williams. For example, if more than two cognitive loads are involved, a bet will have more than two possible payouts; some may find it unfortunate that it is no longer apparent what counts as winning or losing such a bet.Footnote ³³ And one might have the intuition that a bet for A should be understood as a bet for that A is true, which should have two outcomes: it should be won if A is true and lost otherwise. We will now propose a formal generalization of this intuition, even though we believe that the presented notion of L-real-Dutch-bookability may be fruitfully used to deliver valid arguments for norms of rationality in various nonclassical settings. We will illustrate the idea using the classical and Symmetric logics, where cognitive loads (which we assume to be identical to pragmatic loads) directly correspond to truth values; in the following subsection we thus forego any mention of cognitive and pragmatic loads, assuming that is the truth values which straightforwardly determine the payouts.

4.1.1. Truth-value bets

Traditionally, then, we seem to assume that a bet for A is a bet for that A is true. Let us once again tear off the classical shackles and stipulate that for a “truth-value bet” four things are needed: a proposition A, a truth value *, a prize S, and a cost C. We can then speak of a truth-value bet for that A has the truth value *. Note that no matter how many truth values there are, uncovering A's truth value leads to one of just two possible outcomes: either the bettor was right, or (s)he was wrong. It is thus natural to assume that such a bet, which costs C, pays out S if A has the truth value *, and pays out 0 otherwise. Where TV is a nonempty and finite set of truth values, the expected value of a truth-value bet for that A has the truth value * according to the credence $B = { {B_\ast ({\cdot} ) } } _{{\ast}{\in} TV}$ is

(8)$$B_\ast ( A ) ( {S-C} ) + \mathop \sum \limits_{\# \in TV, \# \ne \ast } B_\# ( A ) ( {-C} ) .$$

Sticking with the idea that the fair price of a truth-value bet is the cost C for which the above expression equals 0, we note that regardless of what TV consists of, a fair price for the truth-value bet for that A has the truth value * is $B_\ast ( A ) $. A truth-value Dutch Book against a credence B is then a set of truth-value bets which are fair from the perspective of B, but which lead to B's inevitable loss.Footnote ³⁴

4.6 definition (L-truth-value-dutch-bookable). Suppose a logic L is given in a language ${\cal L}$ with the valuations obtaining values in a finite set TV ⊊ $[ {0, \;1} ] $. Assume credence functions B are of the form $B = { {B_\ast ({\cdot} ) } } _{{\ast}{\in} TV}.$

B is L-truth-value-Dutch-bookable if there are $\vartheta _1, \;\ldots , \;\vartheta _n\in Sent_{\cal L}$, ${\ast} _1, \;\ldots , \;\ast _n\in TV$, and s ₁, …, s _n ∈ ℝ such that for all V ∈ ${\opf V}$ we have

(9)$$\mathop \sum \limits_{i\colon V( {\vartheta_i} ) = {\ast} _i} s_i( {1-B_\ast ( {\vartheta_i} ) } ) + \mathop \sum \limits_{i\colon V( {\vartheta_i} ) \ne \ast _i} s_i( {-B_\ast ( {\vartheta_i} ) } ) < 0.$$

The left sum in (9) refers to the profit from those bets belonging to the Dutch Book which are won at V, and the right one to the profit from those which are lost.

We will now consider two examples. For brevity, when we speak of (just) “a bet for A”, we mean the bet as considered before the current subsection; when we speak of “a bet for that A has truth-value *”, or “a bet for that A is True” (which is shorthand for “a bet for that A has the truth-value 1”), etc., we obviously mean a truth-value bet.

Let us first consider classical logic CL with TV = {1, 0}. Then a bet for that A is False with prize S and cost C is equivalent to the bet for that A is True with prize −S and cost C. Therefore CL-truth-value-Dutch-bookability is reducible to “CL-truth-value-Dutch-bookability exclusively via bets on that propositions are True”. This, in turn, is equivalent to Dutch-bookability (in the typical sense) of B ₁ as a classically conceived credence. So: B = {B ₁, B ₀} is not CL-truth-value-Dutch-bookable iff B ₁ is a classical probability function.

Consider, now, the case of Symmetric Logic SL. Assume thus that TV = {1, 1/2, 0}. A bet for A with the fair price (B ₁(A) + 0.5⋅B _1/2(A))⋅S has the same payout table as the following pair of bets taken together:

• • a bet for that A is true with prize S and cost B ₁(A)⋅S; and

• • a bet for that A has truth value 1/2 with prize 0.5⋅S and cost 0.5⋅B _1/2(A)⋅S,

both of which are truth-value bets which are fair according to {B ₁, B _1/2, B ₀}.

Using this insight we can represent the previous Dutch Book as a truth-value Dutch Book. Consider the credence function displayed in Table 3.

In Table 4, the column labelled ‘*_i’ contains truth values. Each row i of that table defines a truth-value bet for that $\vartheta _i$ has the truth value *_i with the prize s _i, the fair price of which is $B_\ast ( {\vartheta_i} ) \cdot s_i$. It is routine to check that participating in all of these bets yields the loss of 1. It is also routine to check that, again, Table 2 shows that this loss persists no matter what happens: therefore the whole situation is a truth-value Dutch Book against the credence defined in Table 3.

Table 4. A set of bets showing that the credence from Table 3 is SL-truth-value-Dutch-bookable.

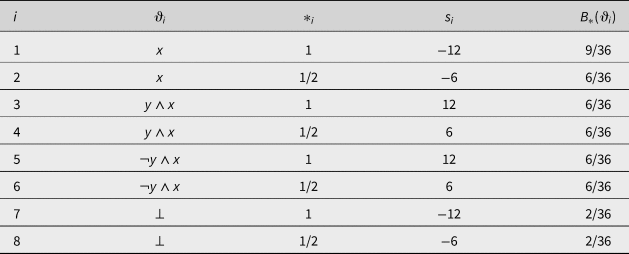
A straightforward generalization of this insight leads to the conclusion that if a credence function is SL -really-Dutch-bookable, it is SL -truth-value-Dutch-bookable.

However, the converse is not true. Assume the language has a single propositional variable x and consider the following credence B (which satisfies (CA)):

That this function is SL-truth-value-Dutch-bookable can be easily seen just from inspection of the top row of that table. Assume unitary prizes. From the perspective of the displayed credence the fair price for the bet for that x is true is 3/4, and the fair price for bet for that x∨¬x is true is 1/2. Buying the first and selling the second bet establishes prior loss of −1/4. In each of the three possible worlds B ends up with a loss:

• • if V(x) = 1, then both bets are won, and so the ultimate loss is the same as the prior loss;

• • if V(x) = 1/2, then both bets are lost, and so the ultimate loss is the same as the prior loss;

• • if V(x) = 0, then V(x∨¬x) = 1, and so the ultimate loss is −5/4.

Therefore B is SL-truth-value-Dutch-bookable. However, notice that B ₁ + 0.5⋅B _1/2 is the following credence:

which we have already seen in Section 3 as a convex combination of two possible worlds (with weights 0.5). By the result of the current paper, we know that B ₁ + 0.5⋅B _1/2 satisfies (SL1)-(SL4), and so is not SL-really-Dutch-Bookable.

We can therefore state the following Fact:

4.7 fact. SL-real-Dutch-bookability implies SL-truth-value-Dutch-bookability; however, the converse does not hold in general.

In the context of truth-value bets we have discussed the classical and Symmetric logics. This is because in these contexts it is easy to think that truth values directly determine bet payouts. Generalizing Definition 4.6 so that it involved cognitive loads poses no formal problems. However, it's not evident for us what kind of betting we would then be modelling: while we find betting for that a proposition has a certain truth value to be somewhat intuitive, we would have to start thinking about betting that a certain proposition has this or that cognitive load, which we are reluctant to do without giving the matter more thought. We leave, then, investigating truth-value-Dutch-bookability in general for future research.