INTRODUCTION
Campylobacter is the principal bacterial agent responsible for gastroenteritis in the developed world, ahead of Salmonella, Escherichia coli, Clostridium spp. and Listeria combined [Reference Adak1]. Campylobacter jejuni, the species responsible for 90% of human campylobacteriosis, is a widespread zoonotic pathogen that is carried by wild and domestic animals, and is common in the environment. It is found in cattle, sheep, pigs, poultry, wild birds, rabbits and other wild mammals, household pets, molluscs, sewage and in natural water sources such as rivers and sea water [Reference Humphrey, O'Brien and Madsen2, Reference Jones3].
Our study is based on a longitudinal sample of 1231 C. jejuni isolates collected over a 3-year period within the Preston postcode district (Lancashire, UK) [Reference Wilson4] supplemented by multilocus sequence typing (MLST) data [Reference Dingle5]. Analysis of MLST data suggests that most (97%) cases were attributable to animals farmed for meat and poultry [Reference Wilson4]. Chicken and cattle were found to be the principal sources of C. jejuni pathogenic to humans, whereas wild animal and environmental sources were responsible for just 3% of disease. The data can be considered as a single realization of a spatio-temporal point process displaying a highly aggregated spatial distribution. As is common in epidemiological studies, the observed point pattern is spatially and temporally inhomogeneous, because the pattern of incidence of the disease reflects both the spatial distribution of the population at risk, and seasonal and long-term trends in incidence. In order to analyse the spatio-temporal pattern of incidence while allowing for these effects, we have used a recently developed statistical approach, detailed and briefly illustrated on a part of the dataset described below by Gabriel & Diggle [Reference Gabriel and Diggle6]. Our paper aims at using their methodology and presenting the epidemiological results.
We first describe separately the spatial and temporal distribution of infections using existing statistical methods that have previously been applied in this context [Reference Eyles7–Reference Sopwith9], then using a recently developed approach [Reference Gabriel and Diggle6] we investigate spatio-temporal clustering and spatio-temporal interaction. This approach allows us to adjust for separate spatial and temporal variation in incidence before testing for spatio-temporal effects, and to determine the spatial and temporal scales over which these effects, if any, occur.
METHODS
Data collection
Cases were defined as being those residents in the Preston postcode district of Lancashire, Northwest England with confirmed C. jejuni infections. The population size in the study region was 403 110 in 2001. A grey-scale representation of the spatial variation in the population density, derived from the 2001 census, is given in Figure 1 a. The Preston postcode district broadly consists of a rural area (north and south-west) and an urban area (south-east), with the city of Preston in the centre. We refer to the most densely populated area, surrounded by a dashed line in Figure 1 a, as the urban area. In our analyses we use both the region as a whole and the urban area. A total of 1549 cases were reported to general practitioners (GPs) or hospitals and sent to the Preston Public Health Laboratory between 1 January 2000 and 31 December 2002. Species-specific PCR primers were used to distinguish isolates of C. jejuni from other species. In 1231 cases the isolate was confirmed as C. jejuni, and MLST was successfully completed at all seven loci. For 969 of these cases a complete follow-up of age, sex and postcode was also available. The date attributed to a case is the date at which the isolate was sent to the laboratory. For the purposes of this study, we analysed the 969 cases (Fig. 1 b) for whom the demographic data and DNA sequencing were complete. Figure 1 c shows the cumulative distribution of the times, in days since 1 January 2000, on which cases were reported. The spatial distribution of cases largely reflects the population at risk, while the temporal distribution suggests a downward trend in incidence over the 3-year study period. The most effective form of display for a spatio-temporal point process data is an animation, repeated viewing of which can yield insights that are not evident in static displays, e.g. the progressive movement of an epidemic through a susceptible population. An animation of our data is available at www.maths.lancs.ac.uk/~rowlings/Chicas/WeeklyCJejuni. This suggests that cases tend to occur in spatio-temporal clusters. Our detailed analysis confirms these initial impressions, while also revealing additional spatial, temporal and spatio-temporal structure, as will be shown in the next section.
Fig. 1. (a) Population density in 2001 (number of people per hectare). (b) Location of infections from 1 January 2000 to 31 December 2002. (c) Cumulative distribution of the times (–––).
Demographic data
The age distribution of C. jejuni infections (Fig. 2) shows three peaks, a familiar pattern in industrialized nations [Reference Allos10]. The first peak, in infants (aged <4 years), is thought to occur for a number of reasons: (i) the immune system is still in development, and (ii) illness is more likely to be reported in infants than in older children and adults. The second and third, smaller peaks occur in young adults (25–34 years) and in the middle-aged (45–54 years).
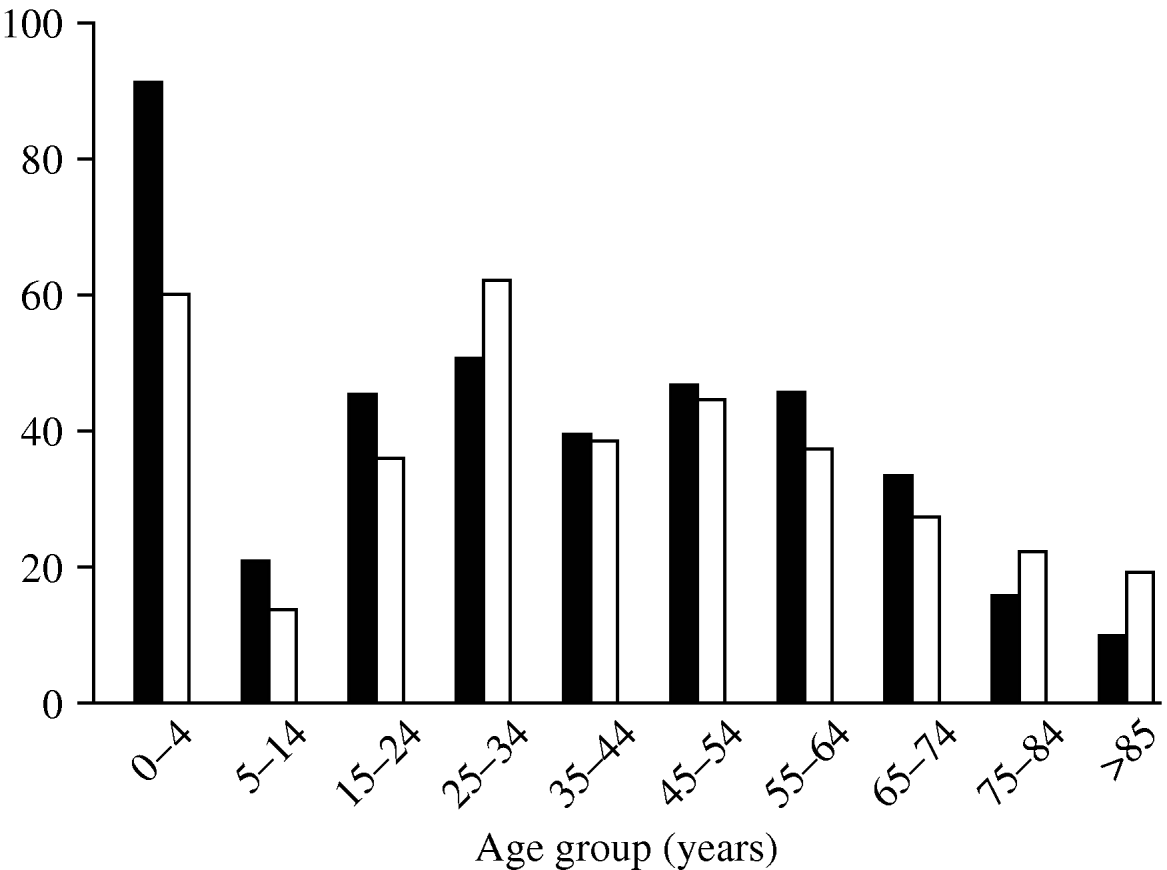
Fig. 2. Rate of cases per 100 000 population by age group during the study period. ▪, Males; □, females.
Males and females show similar age distributions, but total incidence is slightly higher in males.
Statistical analysis
We used a Poisson log-linear regression model to estimate the temporal intensity, μ(t). The empirical pattern of weekly counts showed an overall decreasing trend, γ, while daily counts showed a strong day-of-the-week effect δ(t), with fewer cases observed during the weekend. Exploratory spectral analysis of incidence times suggested a marked annual and 4-monthly periodicity. We therefore fitted a harmonic regression:
where ω=2π/365 is the frequency corresponding to an annual cycle and d(t) identifies the day of the week for day t=1, …, 1096.
Large-scale spatial variation in risk and small-scale spatial clustering were both investigated using case-control methods. Because no population-based matched controls have been included in the study, we considered simulated controls. The 2001 census provides the number of people per Output Area (geographical area used for data collection). We used as controls n 0≈4n locations randomly sampled from the underlying population at risk as follows. We first evaluated the expected number of cases per Output Area:
with N j the number of people living in the jth Output Area. We then randomly sampled n j controls in the jth Output Area, from a Poisson distribution with expectation 4E j. We then estimated a relative risk map by comparing the spatial point distributions of cases and controls, which were assumed to follow inhomogeneous Poisson processes with intensities λ(s) and λ0(s), respectively, where s=(x, y) denotes spatial position. A statistic to test for significant departures from the null hypothesis of constant risk is
where 
(s)=λ(s)/{λ0(s)+λ(s)} is the relative risk at location s. We estimated the relative risk from the data using non-parametric binary regression and calculated the P value of the test by randomly relabelling cases and controls 1000 times to generate a null distribution for T s [Reference Diggle, Zeng and Durr11].
To test for differences in risk over the years 2000, 2001 and 2002, we used the test statistic 
, where 
(s) is an average of the relative risks (s, t) estimated separately for each year and calculated the P value by randomly relabelling the year attributed to each case.
To test for small-scale spatial clustering, we used the test statistic:
as proposed in Diggle et al. [Reference Diggle12]. In equation (2), 
(h) is the estimated inhomogeneous K function [Reference Baddeley, Moller and Waagepetersen13], which measures the clustering between pairs of cases that lie h metres or less apart, while E(h) and V(h) are the mean and variance of (h) calculated from 1000 random relabellings of cases and controls.
This approach was originally developed to test for spatial segregation in two or more subtypes within a multivariate point process of genotyped cases of bovine tuberculosis in Cornwall, UK [Reference Diggle, Zeng and Durr11]. Here, we used the same method to examine spatial segregation in campylobacteriosis cases classified according their mostly likely source (species) of infection [Reference Wilson4].
The spatio-temporal inhomogeneous K function, K ST(h, τ) (STIK function [Reference Gabriel and Diggle6]) measures the distribution of pairs of cases that occur less than or equal to h metres and τ days apart. To test the hypothesis of no spatio-temporal clustering, we compare the STIK function of the data with tolerance envelopes constructed from 1000 simulations of a Poisson process with intensity 
(s)
(t), where the spatial intensity m(s) has been estimated using a Gaussian kernel and the temporal intensity (t) is given by equation (1). To test the hypothesis of no spatio-temporal interaction, we proceed similarly, but with tolerance envelopes constructed by randomly relabelling the locations of the cases holding their notification dates fixed. This hypothesis states that the data are a realization of a pair of independent but otherwise arbitrary spatial and temporal point processes with respective intensities m(s) and μ(t).
RESULTS
Seasonality
Harmonic regression analysis revealed a pronounced periodicity in the incidence of disease at 12-monthly and 4-monthly intervals (Fig. 3). C. jejuni infection peaks in June each year, with secondary peaks in February and October. The fitted incidence is lowest in December, which may reflect reporting bias due to the relative inaccessibility of GPs over the Christmas period. We also observed a decreasing trend in the weekly number of cases over the years, falling by a factor of 1·3 each year.
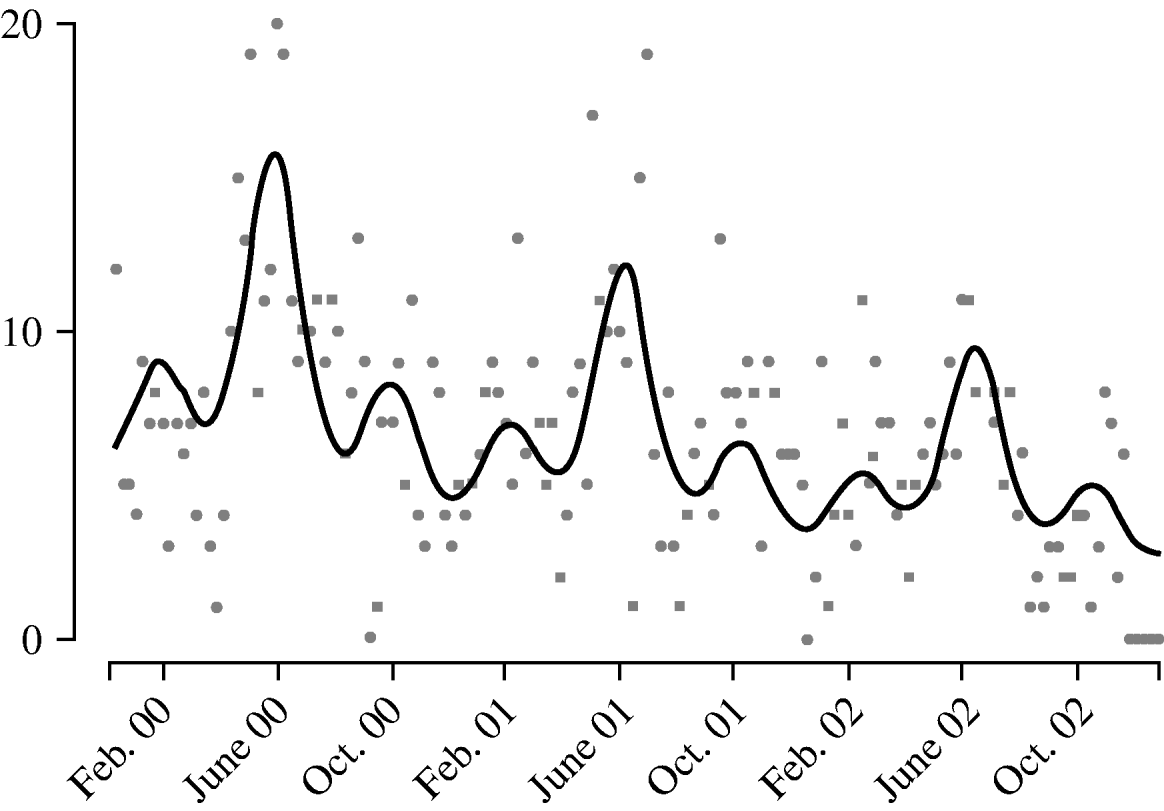
Fig. 3. Weekly report () of Campylobacter jejuni infections compared with fitted regression curve (––).
Spatial clustering
The study region contains a mixture of rural and urban areas, the area of greatest population density being central Preston (Fig. 1 a). Figure 1 b illustrates the spatial incidence of cases. A sample of controls was used to estimate a relative risk map for disease across the region, and to test the hypothesis that incidence is proportional to population density.
Figure 4 a shows local P values associated with this hypothesis; specifically, areas where P<0·025 (coloured white) show significantly higher than average, and areas where P>0·975 (coloured dark grey) significantly lower than average, spatial incidence. Broadly speaking, there is a relatively high risk in the population-dense region of central Preston, and a relatively low risk in the area surrounding the River Ribble and Ribble estuary (south-west). Table 1 indicates that the hypothesis of constant risk at large scales was rejected every year both over the whole region and within the urban area (P<0·05), confirming that incidence is not explained simply by population density.
Fig. 4. Tests for spatial clustering. (a) Local P values of Monte Carlo test for spatial clustering at large spatial scale in the region as a whole. White indicates a statistically significant elevation in the number of cases relative to the number of controls. (b) Clustering statistic (–––) compared with expected values (grey shaded area) under the null hypothesis of constant risk in the urban area.
Table 1. P values associated with tests for spatial clustering
The null hypothesis that incidence is proportional to population density was also rejected at fine scales. Figure 4 b shows, for the urban area, that at distances <1200 m the clustering statistic (black line) lies above the 95% tolerance interval under the null hypothesis (grey shading), indicating clustering of cases. This result was confirmed by a significant result (P=0·001) from the Monte Carlo test for spatial clustering at fine spatial scales. This fine-scale clustering may be partly attributable to multiple cases occurring within the same household, although we were unable to verify this because the spatial distribution of our data is limited to the six-digit postcode.
Spatial segregation
Of the 969 georeferenced cases (619 in the urban area), 386 (230) were associated with cattle, 556 (369) with chicken, 3 (2) with pigs and 3 (1) with water, using a ‘most probable’ allocation rule [Reference Wilson4]. To investigate spatial segregation, we compared the spatial distributions of the cattle-associated cases and the chicken-associated cases. The null hypothesis that the different sources are randomly intermingled was rejected (P=0·032) in the whole region, but not rejected (P=0·094) in the urban area. However, local P values associated with this hypothesis indicate a higher proportion of cases associated with chicken in Leyland (in the centre of the urban area), as shown in Figure 5(a, b). Figure 5 b also shows a higher proportion of cases associated with cattle in the north of the whole region.
Fig. 5. Local P values of Monte Carlo test for spatial segregation in (a) the whole region and (b) the urban area. White indicates a statistically significant elevation in the number of chicken-associated cases relative to the number of cattle-associated cases.
Spatio-temporal variation
Risk maps for the whole region were estimated for each year separately. While the hypothesis of constant risk was rejected for all 3 years, there was evidence of a change in overall risk between the years (P=0·001). In the urban area, there was no evidence of a change in risk between the years (P=0·279).
For the urban area, we compared observed values of the spatio-temporal clustering test statistic against the 95% confidence interval of values obtained under the null hypothesis of constant risk. In Figure 6, diagonal black hatching indicates that the observed values are greater than expected, white regions indicate that they lie within the tolerance interval. This indicates where and when cases are more clustered than expected. Graphical analysis when testing for spatio-temporal interaction highlights the distances and times at which interaction occurs. Figure 6 compares the observed values of the interaction test statistic against the 95% confidence interval of values obtained under the null hypothesis of no interaction. Grey regions indicate that observed values do not lie within the confidence interval. The results suggest spatio-temporal clustering up to a distance of 300 m and a time-lag of 6 days, and spatio-temporal interaction at distances up to 400 m and time-lags up to 4 days. These findings are consistent with the infectious nature of the disease, which may lead to multiple cases from a common source that are relatively close both in space and in time. They also suggest the existence of stochastic structure that cannot be explained by (s)(t).
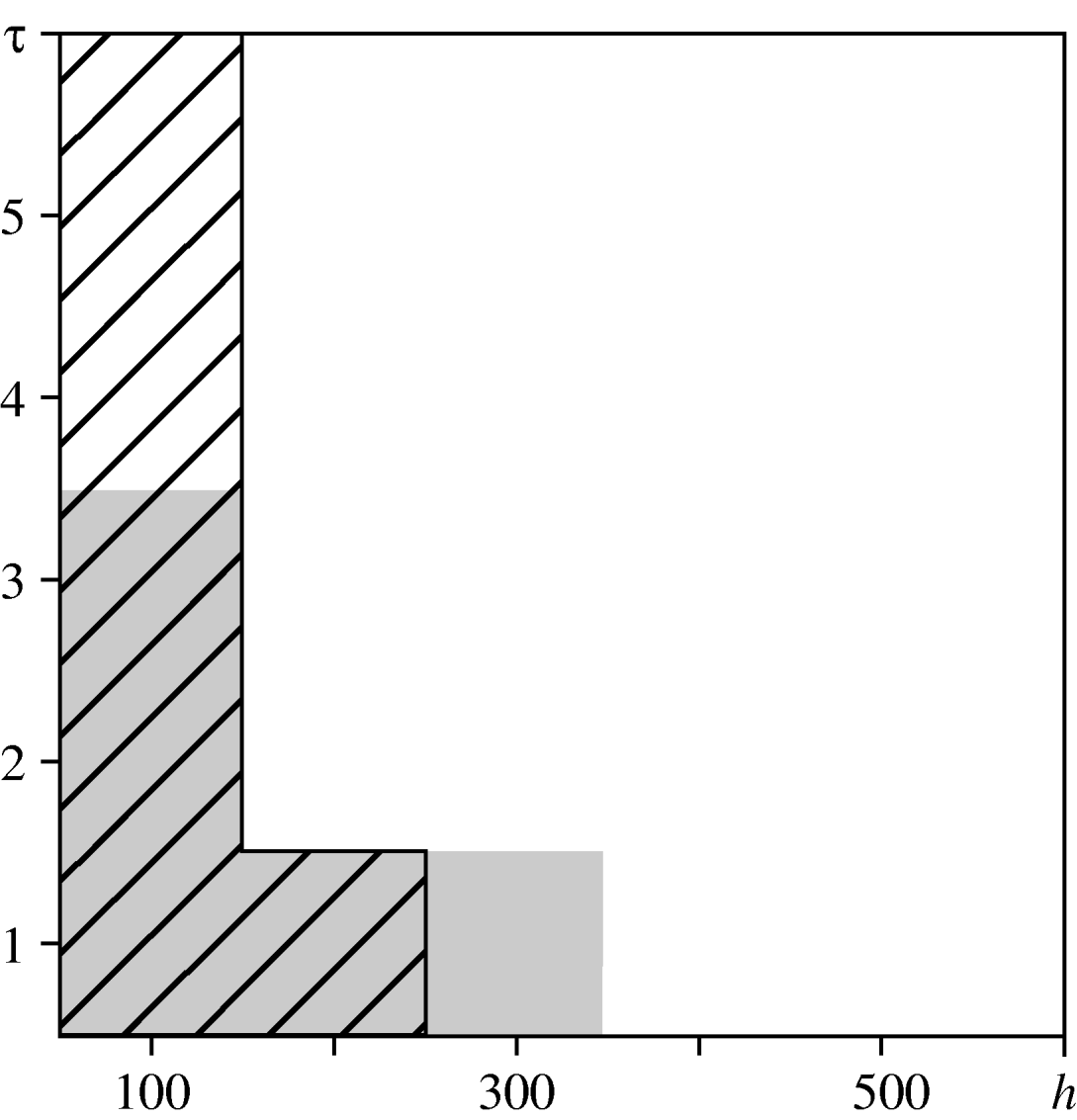
Fig. 6. Spatio-temporal variation in the urban area. Comparison between the test statistics and tolerance envelopes indicating spatio-temporal clustering (diagonal black hatching) and spatio-temporal interaction (grey shading).
DISCUSSION
We have investigated aspects of the temporal, spatial, spatio-temporal and genetic distributions in the incidence of human C. jejuni infections in the Preston postcode district (northwest England).
First, we found that the risk of campylobacteriosis shows strong seasonal variation, rising sharply between spring and summer, with an overall downward trend over the 3-year period covered by the data. The seasonality of incidence reveals two periodicities: a yearly periodicity which causes peaks in late June and a 4-monthly periodicity which causes smaller peaks in February and October.
Second, we found significant small-scale spatial clustering and large-scale spatial variation in incidence, after allowing for the spatial variation in population density over the study region. With respect to the large-scale spatial variation, urban areas showed higher risk of disease than rural areas. This is at first sight counter-intuitive, as food animals are more common in the countryside. It could reflect under-reporting because of less easy access to services, a degree of immunity following previous exposure, or a safer (on average) pattern of food preparation and consumption.
Third, although most cases in our dataset occur as isolated, sporadic events, with no confirmed outbreaks over the 3-year period covered by the data, we found significant small-scale spatio-temporal clustering and interaction over and above the separate temporal and spatial components of variation in risk. This is consistent with a clustering of cases through a combination of multiple cases from a common source and person-to-person infection.
Finally, after classifying the individual cases by their most likely species-of-origin using a recently developed genetic model [Reference Wilson4], we found some evidence of spatial segregation between cases originating in chicken and in cattle; cases originating in chicken are overrepresented in the urban area. This could explain why we found a higher risk of disease in the urban area. Indeed, 80% of retail poultry is contaminated by C. jejuni in the UK [Reference Corry and Atabay14] and people in urban areas mainly buy such commercial chicken meat.
Our results are broadly consistent with, but more detailed than, those described in previous work relating to campylobacteriosis in northwest England [Reference Sopwith9, Reference Sopwith15]. We used Monte Carlo tests for spatio-temporal clustering and for spatio-temporal interaction, based on the space–time inhomogeneous K function. Application of these tests to the C. jejuni data suggests a combination of spatially and temporally localized variations in risk, and small-scale spatio-temporal clusters of cases. In reaching these conclusions, we have of necessity made a pragmatic distinction between heterogeneity and clustering, since these two phenomena are not empirically distinguishable. We have chosen to identify as heterogeneity the estimated spatial and temporal variations in risk, averaged over time and space, respectively, and to identify as clustering any residual spatio-temporal structure that cannot be explained by this heterogeneity. Our empirical findings are consistent with there being both unmeasured socio-economic or environmental risk factors for the disease, and foodborne infections leading to multiple cases that are close in both space and time.
ACKNOWLEDGEMENTS
This work was funded by the Department for Environment, Food and Rural Affairs as part of the Veterinary Training Research Initiative, and by the National Centre for Zoonosis Research.
DECLARATION OF INTEREST
None.
