Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T02:42:06.275Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of air movement and atmospheric conditions on the heat loss from a cylindrical moist body

Published online by Cambridge University Press:  15 May 2009

Alan J. Canny  and
C. J. Martin
Alan J. Canny
Affiliation:
From the Lister Institute of Preventive Medicine
C. J. Martin
Affiliation:
From the Lister Institute of Preventive Medicine
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is emphasized that as heat exchange is controlled by the temperature of that boundary layer of molecular dimensions which separates a cooling body from its environment and from which evaporation occurs, attempts to relate heat loss with internal temperature have resulted only in empirical formulae. A rational formula involving the temperature of the evaporating surface is suggested, and it is shown how in the case of a system of sufficient simplicity all the terms can be either measured or derived from experiments.

The results of experiments with a small moistened cylinder are detailed illustrating the effect of wind velocity upon evaporative and convective heat loss under the one condition when the evaporating surface remains at constant temperature notwithstanding variations in wind, namely, when the whole system has been cooled to wet-bulb temperature. Evaporative loss is found to vary as V0.65, convective as V0.70.

Experiments are next described showing the effect of wind upon evaporative and convective losses when, the internal temperature being constant, the temperature of the evaporating surface fluctuates in consequence of varying wind velocity. Heat loss now varies very closely as V0.5 at velocities greater than 1 m./sec. At velocities below 1 m./sec. the same relation of heat loss to velocity obtains if due allowance be made for natural convection. This square root function is fortuitous, and heat loss varied between the square root and cube root of the velocity as the internal conductivity was diminished.

Attention is drawn to the impossibility of forming general conclusions from observations on any particular system, as the way in which the rate of heat loss varies with the velocity of the wind depends not only upon the internal conductivity of the system but also on its size and shape.

Observations are described showing the influence of varying the internal temperature on total and evaporative heat loss with constant wind velocity and constant atmospheric conditions. These experiments furnish data from which the surface temperature can be derived from measurements of evaporation, and show that the temperature of the surface and the rate of loss of heat by convection are both linear functions of the internal temperature at any one wind velocity. They also show that the values of the constants of the system derived from experiments at the temperature of the wet bulb are applicable when the cylinder is heated.

An analysis of the results of the experiments with varying internal temperature indicates that the temperature of the evaporating surface (ts) is related to the internal temperature (t1) and that of the wet bulb (tw) by the expression 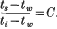The value of C with varying wind velocity is ascertained by experiments, thus affording another means of arriving at the temperature of the evaporating layer. Values of ts obtained in this way are compared with those determined by observing the rate of evaporation and show reasonable agreement.

It is shown how, knowing the temperature of the evaporating layer, the constants of the system employed and the effect of velocity of wind upon heat exchange, the rate of loss of heat by evaporation and by convection under given conditions can be predicted. Instances of the agreement between predicted and observed values are given.

From the formula representing the influence of atmospheric conditions on heat loss it can be shown, by calculation, that if the wet-bulb temperature remains constant considerable variations in the temperature of the dry-bulb influence but slightly the heat loss from the moist cylinder.

It will be seen that the analysis of the effects of environmental changes on the heat loss from a simple physical system such as was used presents no serious difficulties. Such an analysis, unfortunately, does not enable deductions to be made with reference to systems of different physical characteristics. How observations on such systems can be related in other than a qualitative manner to the effects of corresponding changes on living creature differing in size and shape and degree of moistening of their surfaces is not clear. When account is taken of the ability of living beings to alter the vascularity of their surface tissues and so to vary the temperature of the body surface while other factors remain constant, the difficulties in relating the cooling of any physical system to the loss of heat from animals become painfully apparent.

The most hopeful method of assessing the effect of air movement and atmospheric conditions on the heat loss from the human body seems to be in terms of a subjectively determined standard such as the effective temperature scale of Houghton & Yaglou. The validity of such a scale has received support from observations by Houghton et al. (1924) and Vernon & Warner (1932) on the relation of pulse rate, body temperature, metabolism and other physiological variables to “effective temperature”.

Type
Research Article
Information
Journal of Hygiene , Volume 39 , Issue 1 , January 1939 , pp. 60 - 89
Copyright
Copyright © Cambridge University Press 1939

References

REFERENCES

Aldrich, L. B. (1928). “A study of body radiation.” Smithson. Misc. Coll. 81, no. 6.Google Scholar
Bedford, T. (1937). “Measurement of environmental warmth.” Trans. Instn Min. Engrs, 94, 76.Google Scholar
Boussinesq, J. (1901). “Sur le pouvoir refroidissant d'un courant liquid ou gazeux.” C. R. Acad. Sci., Paris, 133, 257.Google Scholar
Dalton, J. (1802). “Experimental essays on the constitution of mixed gases; on evaporation, etc.” Mem. Manchr. lit. phil. Soc. 5, 535.Google Scholar
Fishenden, Margaret & Saunders, O. A. (1930). “The calculation of convection heat transfer.” Engineering, p. 177 (8 08.).Google Scholar
Haldane, J. S. (1905). “The influence of high air temperatures.” J. Hyg., Camb., 5, 494.Google Scholar
Haldane, J. S. (1929). “Atmospheric conditions in Indian coal mines” Trans. Instn Min. Engrs, 76, 340.Google Scholar
Heymann, B. (1904). “Über den Einfluss des Windes auf die Wärmeabgabe todter Objecte.” Z. Hyg. InfektKr. 46, 196.Google Scholar
Hill, L., Griffith, O. W. & Flack, M. (1916). “The Measurement of the rate of heat loss at body temperature by convection, radiation and evaporation.” Philos. Trans. B, 207, 183–220.Google Scholar
Hill, L., Vernon, H. M., & Hargood-Ash, D. (1922). “The kata-thermometer as a measure of ventilation.” Proc. roy. Soc. B, 93, 198.Google Scholar
Houghton, F. C. & Yaglou, C. P. (1923). “Determining equal comfort lines.” Trans. Amer. Soc. Heat. Vent. Engrs, 29, 163.Google Scholar
Houghton, F. C., Yaglou, C. P. & Sayers, R. R. (1924). “Effective temperatures and their application to mining.”. Bur. Mines Rep. Invest. no. 2563.Google Scholar
King, L. V. (1914). “On the convection of heat from small cylinders in a stream of fluid: determination of the convection constants of small platinum wires with applications to hot-wire anemometry.”. Philos. Trans. A, 214, 373.Google Scholar
King, L. V. (1915). “On the precision measurement of air velocity by means of the linear hotwire anemometer.” Phil. Mag. 29, 556.CrossRefGoogle Scholar
Martin, C. J. (1923). “Work and hot climate.” Med. J. Aust. p. 377, 29 09.Google Scholar
Martin, C. J. (1930). “Thermal adjustment of man and animals to external conditions.” Lancet, 2, 561, 617 and 673.CrossRefGoogle Scholar
Ower, E. (1927). The Measurement of Air Flow. London: Chapman and Hall.Google Scholar
Rees, J. P. (1927). “The effect of ventilation on the cooling power of the air.” Trans. Instn Min. Engrs, 71, 6, 470–7; 72, 6, 331–4.Google Scholar
Russell, A. (1910). “The convection of heat from a body cooled by a stream of fluid.” Proc. phys. Soc. 22, 432.Google Scholar
Schierbeck, N. P. (1895). “Über die Bestimmung des Feuchtigkeitsgrades der Luft für physiologische und hygienische Zwecke.” Arch. Hyg., Berl., 25, 196.Google Scholar
Schuckmann, Von (1904). “Der Einfluss der Windgeschwindigkeit auf die Wärmeabgabe.” Z. Hyg., Berl., 46, 183.Google Scholar
Skinner, S. (1921). “The wet and dry bulb hygrometer.” Proc. phys. Soc. 34, LX.Google Scholar
Stefan (1874). “Versuche über die Verdampfung.” S. B. Akad. Wiss. Wien, Math. Nat.-Wiss.Kl., 68, 385.Google Scholar
Vernon, H. M. & Warner, C. G. (1932). “Influence of the humidity of the air on capacity for work at high temperatures.” J. Hyg., Camb., 32, 431.Google Scholar
Yaglou, C. P. (1926). “Thermal index of atmospheric conditions and application to industrial life.” J. Industr. Hyg. 8, 5.Google Scholar
Yaglou, C. P. (1927). “Temperature, humidity and air movement in industries: the effective temperature index.” J. Industr. Hyg. 9, 297.Google Scholar
Yaglou, C. P. (1927). “Comfort zone for men stripped to the waist.” J. Industr. Hyg. 9, 251.Google Scholar