INTRODUCTION
Dengue virus, which is transmitted by Aedes mosquitoes, infects more than 50 million people annually [1]. Aedes mosquitoes breed mainly in artificial water containers, such as water storage tanks, jars, and discarded tyres [Reference Lambdin2–Reference Nathan and Knudsen5]. Infection with dengue virus manifests as a spectrum of illnesses, ranging from the rarely fatal dengue fever (DF) to the potentially fatal dengue haemorrhagic fever (DHF). Since DHF was first recognized in the 1950s in South East Asia, it has become a major threat to global public health, giving rise to 500 000 hospitalizations annually [1].
Interestingly, the mean age of DF/DHF patients has been shifting in many countries [Reference Guha-Sapir and Schimmer6, Reference Teixeira7]. For example, the mean age of DF patients has steadily increased in Singapore [Reference Ooi, Goh and Chee Wang8, Reference Egger9], and the mean age of DHF patients also increased in Thailand [Reference Chareonsook10]. It was hypothesized that, at least in Singapore and Thailand, the increased mean ages of DF/DHF patients was due primarily to decreasing mosquitoes (or more generally, lower transmission intensity) as a result of successful vector control [Reference Egger9, Reference Nagao and Koelle11, Reference Thammapalo12] (Appendix 1). Indeed, it is a long-held assumption that the mean age of patients of an acute infectious disease is negatively correlated with transmission intensity [Reference Anderson and May13]. However, before applying this theorem to dengue, the complex aetiology of DHF must be reviewed. Dengue virus consists of four serotypes, and most DHF cases occur in the presence of a pre-existing heterotypic antibody [Reference Hawkes14, Reference Halstead, Nimmannitya and Cohen15]; this is known as antibody-dependent enhancement. Even with this peculiar aetiology, secondary infections are most likely to occur at younger ages in areas of more intense transmission than in areas of milder transmission. Therefore, the mean age of DHF patients and transmission intensity are expected to be negatively related, even though these two variables may not be in a strictly inverse mathematical relationship. Consistent with this hypothesis, a negative relationship between an entomological index and mean age of DHF patients was reported [Reference Thammapalo12].
However, the increase in the mean age of dengue illnesses in Thailand could also be explained by the changing demographic structure [Reference Cummings16]. A larger proportion of newborns and small children in the overall population could increase the proportion of young patients; this naive population may also facilitate transmission and decrease the mean age of patients indirectly. In contrast, a higher mean age in the overall population may increase the proportion of older patients, thereby increasing the mean age of patients.
The reason for the shifting mean age of dengue illnesses is important, not only from a purely scientific viewpoint, but also from a public health standpoint, because the mean age of DHF patients could be a useful indicator for vector control if it reflects transmission intensity. The present study therefore compared mosquito abundance and demographic variables to determine their contributions to the mean age of DHF patients.
METHODS
Study site and geographical data
We obtained entomological, demographic, socioeconomic, and climate data from each of the 91 districts in northern Thailand that we had previously reported upon [Reference Nagao17] (Fig. 1). The study site spread 580 km north–south by 460 km east–west. We used the geographical information system Mapinfo Professional (Mapinfo, USA). Digital map data was obtained from Mapinfo Thailand.

Fig. 1. Study site in northern Thailand. The 90 districts in northern Thailand studied in the present report are indicated by shading.
Epidemiological data of DHF
Districts in Thailand report the number of DHF cases (including dengue shock syndrome) to the Ministry of Public Health (MPH). From the MPH, we obtained the age-stratified annual number of DHF patients for 90 of the 91 districts. The remaining one district was not identified in this data, for unknown reason. From this data, the mean age of DHF cases was calculated as the midpoint of each age group (e.g. 12·5 years for the 10–14 years age group) weighted by the proportion of cases in the age group. The distribution of mean age of DHF patients was highly skewed, and hence was not suitable for linear regression analysis. Therefore, crude mean age of DHF patients (cMA-DHF) was transformed into normalized mean age of DHF patients (nMA-DHF), as in:
where the optimal λ was selected by the Box–Cox method [Reference Box and Cox18].
Entomological data
We obtained results of two independent entomological surveys. In the first survey, community volunteers surveyed diverse villages in the 91 districts in northern Thailand in 1994, 1995 and 1996 [Reference Suwonkerd and Prachakwong19]. In the second survey, public health officials surveyed the central villages of 914 districts in Thailand in April in 2002, 2003 and 2004 [Reference Thammapalo12]. We used the records from northern Thailand extracted from the second survey, to be consistent with the first survey. In our analysis, the results from these two periods (1994–1996 and 2002–2004) were aggregated individually. Aedes abundance was represented by ‘house index’ which measures the percentage of premises positive with water containers infested with Aedes larvae/pupae. Larval indices, including house index, have limitations in their capacity to reflect the density of adult mosquitoes that determines transmission intensity most critically [Reference Focks and Chadee20]. However, we failed to find any data representing the transmission intensity, other than house index, to cover such a wide area as our study site.
Demographic data
District-level age-stratified demographic data was obtained from the National Statistical Office (NSO) of Thailand. From this data, the average age of the district's entire population (‘district average age’) was estimated as the sum of the mid-point of each age group weighted by the proportion of population in this age group. The NSO data for 1995 and that for 2003 were used for the two periods, 1994–1996 and 2002–2004, respectively. The birthrate (per 1000 population) was delineated from the National Rural Database 2c (NRD2c) which was derived from biannual national census [Reference Jitsuchon-S, Bedi and Simler21]. The birthrate averaged between 1994 and 1996 was used for the period of 1994–1996, while the birthrate averaged between 2002 and 2004 was used for the 2002–2004 period.
Socioeconomic data
Socioeconomic variables are known to affect dengue transmission intensity [Reference Spiegel22–Reference Thammapalo24]. Our analysis which employed the NRD2c revealed that mosquito larval indices (including the house index) and the inverse of the mean age of DHF patients (which we assumed to represent transmission intensity) correlated positively with the prevalence of public large water wells, but negatively with the prevalence of private small water wells [Reference Nagao17, Reference Nagao25]. These two socioeconomic variables averaged between the 1994 NRD2c and 1996 NRD2c were used for the 1994–1996 period, while those averaged between the 2002 NRD2c and 2004 NRD2c were used for the 2002–2004 period.
Climate data
Climate exerts a complex effect on dengue transmission intensity. High temperature increases transmission intensity by enhancing mosquito survival [Reference Chang26] and hastening viral incubation in mosquitoes [Reference Watts27]. However, extremely high temperature increases the mortality of mosquito eggs [Reference Juliano28], and adult mosquitoes [Reference Yang29]. Similarly, aridity decreases mosquito longevity [Reference Alto and Juliano30], but may increase the need for household water containers and consequently the number of breeding sites. Previously, we reported that average pan evapotranspiration (APET), which measures the water that evaporates from a standardized pan [31], predicts the mean age of DHF cases better than any other single climatic variable in Thailand [Reference Nagao25]. Furthermore, evapotranspiration quantifies aridity by taking into account numerous climatic variables: solar radiation, temperature, humidity, and wind speed [Reference Penman32, Reference Monteith33]. Therefore, our present analysis used only APET to represent climatic conditions relevant to the mean age of DHF patients. Monthly APET values at 89 weather stations in Indochina were obtained from the University Corporation for Atmospheric Research [34], averaged through the two periods individually, and interpolated to the geographical centre of each district using inverse distance weighting [Reference Nagao25].
Identification of geographical gradient of district attribute variables
We created a density (thematic) map for each district attribute variable. To interpret the pattern in each density map objectively, we developed a methodology to quantify the direction and strength of geographical gradients of the district attributes (Appendix 2).
Statistical analysis
The relationships between normalized mean age of DHF patients and entomological or demographic variables at the district level were evaluated by conventional linear regression analysis. The effects of socioeconomic/climatic covariates were adjusted in multivariate analyses. We controlled for possible biases deriving from spatial autocorrelation (i.e. districts near each other tend to exhibit similar values), by using the following spatial regression analysis [Reference Anselin and Hudak35]:
where X and Y denote independent and dependent variables, respectively, β denotes the regression coefficient vector, ρ denotes the spatial autoregressive parameter, and W represents the row-standardized spatial neighbourhood matrix. Each element of the spatial neighbourhood matrix is assigned the value ‘1’ if the given pair of district centres are within a predefined distance (‘neighbourhood distance’), and ‘0’ otherwise. As a result, WY expresses a spatially lagged dependent variable. Stata v. 9·0 (Stata Corporation, USA) was used for statistical analyses. Software for the spatial regression analysis was provided by Maurizio Pisati. The data and software prepared for the present study are available from our website (see Appendix 3).
RESULTS
Geographical gradient of district attributes
The data used in our analysis are summarized in Table 1. The attributes examined in our analysis varied from district to district greatly, as shown in Table 1. A total of 13 388 cases of DHF were reported during the 1994–1996 period, while 10 179 cases were reported between 2002 and 2004. The mean and range of house index were very different between the two periods. This may reflect the fact that more heterogeneous villages were surveyed in the 1994–1996 survey than in the 2002–2004 survey, the latter of which investigated only the district centres, and only in April.
Table 1. Attributes of 90 districts in northern Thailand

APET, Average pan evapotranspiration; DHF, dengue haemorrhagic fever.
The incidence of DHF (magnitude and distribution) varied from year to year (Fig. 2). In contrast, the mean age of DHF patients was consistently higher in the northwestern districts throughout the two study periods (Fig. 3), whereas the vector abundance was consistently higher in the southeastern districts (Fig. 4). The spatial trends of district average age and birthrate were not remarkable (Fig. 5a, b). Public large wells were common in the southeastern districts (Fig. 5c), whereas private small wells were more common in the northern districts (Fig. 5d); APET was high in southeastern districts (Fig. 5e). These observations were confirmed by spatial gradient analysis (Fig. 6). In both periods, APET, public large wells, and house index showed statistically significant gradients to the southeast, whereas mean age of DHF patients exhibited gradients in the opposite direction.

Fig. 2. Spatial and temporal heterogeneity in incidence of dengue haemorrhagic fever (DHF). The annual incidence of DHF was estimated for each of 90 districts in northern Thailand.

Fig. 3. Spatial and temporal heterogeneity in mean age of patients with dengue haemorrhagic fever (DHF). The mean age of DHF patients reported was estimated for each of 90 districts in northern Thailand.

Fig. 4. Spatial and temporal heterogeneity in vector mosquito abundance. The house index (i.e. percentage of premises positive with water containers infested with Aedes larvae/pupae) was averaged at the district level. Since the survey conducted between 1994 and 1996 and the survey conducted between 2002 and 2004 were based upon different schemes, keys are presented for the individual periods.

Fig. 5. Spatial heterogeneity in demographic, socioeconomic and climatic variables. (a) Average age of the entire population of each district (‘district average age’), (b) birthrate (in a population of 1000), (c) per capita number of public large wells, (d) per capita number of private small wells, and (e) average pan evapotranspiration (APET, mm/day) representing aridity are shown for the 1994–1996 period. The spatial trend of each variable was largely similar in the 2002–2004 period.

Fig. 6. Geographical gradient of district attributes. The geographical gradients of the district-level attribute variables were estimated using the method described in Appendix 2. The gradient direction (θ), the strength of gradient (R), and its statistical significance (P) are presented in parentheses. The length of each arrow represents R. Variables which did not show significant gradients were omitted (i.e. birthrate in both periods; district average age in the 2002–2004 period).
Normalization of mean age of DHF patients
The variable crude mean age of DHF patients was transformed into normalized mean age of DHF patients by applying equation (1) (λ=−0·499 for 1994–1996; λ=−0·157 for 2002–2004). This transformation does not affect the rank (see Supplementary Fig. 1, available online).
Conventional regression analysis
Table 2 presents the result of conventional (i.e. non-spatial) univariate regression analysis. It was shown that normalized mean age of DHF patients was correlated with house index in both periods (1994–1996: R 2=33, P<0·001; 2002–2004: R 2=0·22, P<0·001), and more weakly with district average age only in the 1994–1996 period (R 2=0·097, P=0·003); however, normalized mean age of DHF patients was not correlated significantly with district average age in the 2002–2004 period (P=0·297), or with birthrate in either period (1994–1996: P=0·692; 2002–2004: P=0·183) (see also Supplementary Fig. 2, online).
Table 2. Conventional univariate regression analysis to explain normalized mean age of dengue haemorrhagic fever patients
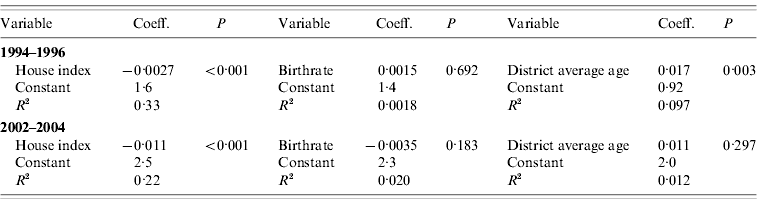
Coeff., Coefficient.
As shown in Table 3, conventional multivariate analysis revealed that the normalized mean age of DHF patients was correlated significantly with house index in both periods (1994–1996: P=0·002; 2002–2004: P=0·038). However, in either period, normalized mean age of patients was not correlated with birthrate (1994–1996: P=0·214; 2002–2004: P=0·432) or district average age (1994–1996: P=0·877; 2002–2004: P=0·346).
Table 3. Conventional multivariate regression analysis to explain normalized mean age of dengue haemorrhagic fever patients

Coeff., Coefficient; APET, average pan evapotranspiration (mm/day).
Spatial regression analysis
The largest minimum distance between districts was 54 km, while the smallest maximum distance was 287 km. Therefore, we defined the neighbourhood distance as 100 km. Spatial univariate regression analysis showed that, in both periods, normalized mean age of DHF patients was significantly correlated with house index (1994–1996: P<0·001: 2002–2004: P=0·029), but not with birthrate (1994–1996: P=0·515; 2002–2004: P=0·362) or district average age (1994–1996: P=0·272; 2002–2004: P=0·947) (Table 4). Spatial multivariate regression analysis supported these results (Table 5). During the 1994–1996 period, normalized mean age of DHF patients was correlated significantly with house index (P<0·001) but not with birthrate (P=0·491) or district average age (P=0·332). During the 2002–2004 period, normalized mean age of patients showed a marginally significant correlation with house index (P=0·090), although correlations with birthrate and district average age were clearly non-significant (P=0·379 and P=0·646, respectively). Repeating these analyses with an alternative neighbourhood distance of 200 km did not affect the results qualitatively (see ‘Log of statistical analyses’ in Appendix 3).
Table 4. Spatial univariate regression analysis to explain normalized mean age of dengue haemorrhagic fever patients

Coeff., Coefficient.
Table 5. Spatial multivariate regression analysis to explain normalized mean age of dengue haemorrhagic fever patients

Coeff., Coefficient; APET, average pan evapotranspiration (mm/day).
DISCUSSION
The mean age of patients of dengue illnesses has shifted in many countries. Two apparently opposing hypotheses have been proposed as the mechanism underlying this phenomenon, i.e. mosquito abundance [Reference Nagao and Koelle11] vs. demographic structure [Reference Cummings16]. However, to our knowledge, no study has compared the contribution of these two factors to the age of dengue patients, using entomological and demographic data. By using actual entomological/demographic data, the present study demonstrated that the mean age of DHF patients was correlated with mosquito abundance, but not with the demographic variables evaluated, after controlling for potential confounders (socioeconomics, climate, or spatial autocorrelation). Thus, mosquito abundance appears to exert more influence on the mean age of DHF patients than demographic factors, in our study site and period.
Shift in age-dependent exposure to mosquitoes also has been proposed as an explanation for the change in the mean age of dengue patients [Reference Ooi36]. A decrease in the exposure in infants and younger children, for example due to the widespread use of air conditioners in households, would most likely increase the age of infections, thereby raising the mean age of patients. This explanation should be tested in epidemiological studies.
Identification of spatial and/or temporal clusters of dengue would assist not only understanding of disease dynamics but disease control programmes [Reference Mammen37–Reference Hu39]. However, our study site was irregularly shaped and contained gaps (Fig. 1), which hindered such analyses. Alternatively, we focused upon geographical gradient. A limited number of dengue/Aedes studies have paid attention to geographical gradient [Reference Tsuda40, Reference Carbajo41], which has been a frequent topic in ecological and public health studies [Reference Jokelainen42, Reference McKinnon43]. However, almost all of the previous studies used only east–west or north–south directions. By examining all directions, the present study revealed that the geographical gradient of mosquito abundance showed a similarity to that of public large wells, but was in opposite direction to the gradient of private small wells. We hypothesize that use of public water wells requires water storage in individual households, which would increase Aedes abundance, whereas use of private wells would decrease the need for household water storage. Interestingly, the geographical gradient of aridity (i.e. APET) was correlated positively with public large wells, but negatively with private small wells. These correlations between mode of water use and climate may be explained as follows. Because underground water is located in deep aquifers in arid regions, large wells are needed. Digging such large-scale water wells requires considerable investment, which accounts for the high number of public wells in arid districts (Fig. 5). Consequently, Aedes abundance is affected by the mode of water use, the latter of which is determined by climate. An alternative (but not mutually exclusive) explanation for the positive relationship between aridity and Aedes is that dry conditions necessitate storing rainwater in individual households [Reference Pontes44].
Taken together, our results show that the mean age of DHF patients is associated with vector mosquito abundance rather than demographic factors. In the present study, the spatial spread was limited. In particular, our study site did not include Bangkok that was reported to be the epicentre of dynamic spread of dengue [Reference Cummings45]. In addition, the second entomological survey, which surveyed only the district centres, did not capture the heterogeneity in the districts completely (Table 1). This reduced sensitivity of the second entomological survey may account for the marginally significant correlation in the spatial multivariate regression (Table 5). Therefore, similar studies should be conducted in a wider area, including Bangkok, surveying both urban and rural areas. However, the results of the present study suggest that the mean age of DHF patients may be an indicator of transmission intensity in endemic countries.
APPENDIX 1
Negative relationship between mean age of DHF patients and dengue transmission intensity
Transmission intensity can be represented by the basic reproduction number R 0, i.e. the number of new infections originating from one infectious individual in a susceptible population. R 0 is considered to be proportionate to the vector abundance [Reference Macdonald46]. There have been numerous attempts to estimate R 0 [Reference Marques, Forattini and Massad47–Reference Massad49]. We proposed expressing R 0 in a stable endemic state as a function of the mean age of DHF patients (A DHF) according to the following equation [Reference Nagao and Koelle11]:
![\eqalignno{ \hskip-3pt R_{0} \equals \tab {H \over {A_{{\rm DHF}} }}\left[ {\left( {{{p_{\setnum{1}} } \over {\sum\limits_{i} {p_{i} } }} \times {1 \over 4}} \right) \hskip-1pt \plus \hskip-1pt \left( {{{p_{\setnum{2}} } \over {\sum\limits_{i} {p_{i} } }} \times \left( {{1 \over 4} \plus {1 \over 3}} \right)} \right)} \right. \cr \tab \left. { \plus \left( {{{p_{\setnum{3}} } \over {\sum\limits_{i} {p_{i} } }} \times \left( {{1 \over 4} \plus {1 \over 3} \plus {1 \over 2}} \right)} \right) } \right. \cr \tab \left. {\plus \left( {{{p_{\setnum{4}} } \over {\sum\limits_{i} {p_{i} } }} \times \left( {{1 \over 4} \plus {1 \over 3} \plus {1 \over 2} \plus 1} \right)} \right)} \right] , \tab](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921000846614-0337:S0950268811000653:S0950268811000653_eqn3.gif?pub-status=live)
where H denotes host life expectancy, and p i denotes the probability of DHF developing in the ith infection. By incorporating realistic parameters (H=70 years, p 1=0·002, p 2=p 3=p 4=0·04) based upon an epidemiological study [Reference Sangkawibha50], equation (3) can be simplified as:
This relationship is depicted as open circles in Supplementary Figure 3 (online). An individual-based model was built with the same parameters [Reference Thammapalo12]; the relationship between A DHF and R 0 using this simulation is depicted as the closed circles in Supplementary Figure 3 (online). The similarity between A DHF−R 0 relationships predicted by these different methods supports our assumption that A DHF can be used as a reverse indicator of R 0, at least in terms of rank.
APPENDIX 2
Identification of the spatial gradient of an attribute variable
We developed a methodology to identify the spatial gradients of district-level attribute variables. The location of the each district was expressed as (x,y) on the Universal Transverse Mercator (UTM) coordinate system, where x and y are longitude and latitude, respectively (see Supplementary Fig. 4, online). To search for the gradient direction of an attribute variable A, an axis was rotated which intersects the x axis of UTM with an angle of θ. The (x,y) was projected to this rotating axis. As a result, the coordinate of the district on this rotating axis (L) can be expressed by x, y, and θ as:
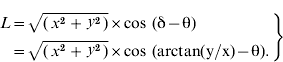
While θ was increased incrementally from −π (−180°) to +π (180°), the correlation coefficient (R) between A and L was recorded for each θ. The θ that generated the largest R (i.e. strongest correlation) was assumed to be the gradient of the variable A, whereas R represented the gradient strength.
APPENDIX 3
Data files available from our website
The following data files used in the present study are available at: http://www.geocities.jp/vector_borne_diseases/gradient/gradient_of_dhf.html.
Attributes of each of the 90 districts (amphoes).
Age-stratified number of DHF patients reported from the 90 districts of northern Thailand.
Log of statistical analyses.
Software code developed for the geographical gradient analysis.
Input data for the gradient analysis.
Output data files from the gradient analysis.
NOTE
Supplementary material accompanies this paper on the Journal's website (http://journals.cambridge.org/hyg).
ACKNOWLEDGEMENTS
We are grateful to Maurizio Pisati for proving spatial analysis software, and to Pongsvas Svasti for his assistance in the analysis of the NRD2c database.
DECLARATION OF INTEREST
None.













