Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T04:31:06.246Z Has data issue: false hasContentIssue false
  • English
  • Français

The evaluation of bactericides

Published online by Cambridge University Press:  15 May 2009

E. R. Withell
E. R. Withell
Affiliation:
from the Department of Pharmacy and Biology, Central Technical College, Birmingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Rideal-Walker and Chick-Martin tests depend on end-point methods for comparing bactericides. End-point methods have a number of disadvantages: (1) It is difficult, if not impossible, to estimate end-points accurately. (2) The nature of the test demands a standard time. The results at any standard time will be arbitrary. If the sensitivity of the organisms varies in the two solutions tested, the coefficients obtained will vary with the time chosen as standard. It is impossible to estimate the manner in which the survivor times of the organism are distributed, by end-point methods, and therefore the standard tests in current use do not ascertain whether the result is arbitrary or not. This can only be appreciated if the tests are repeated using different times.

Apart from the difficulties associated with end-points, the coefficients obtained in the present tests are calculated from one concentration of phenol and one concentration of test bactericide. This is also an arbitrary value, for the relative activity of two bactericides will depend on relative values of the concentration exponent, n, for each bactericide; if both phenol and the test bactericide have identical values of n the coefficients will be the same at all concentrations which are compared, but if values of n are different then different coefficients will be obtained for every different concentration compared. As a corollary, unless the value of n for the test bactericide is the same as that of phenol, it is illogical to transfer the phenol coefficient obtained at one concentration to the pure substance, for this procedure implies that the phenol coefficient applies to any concentration of the test bactericide. This is only true when the concentration coefficients of phenol and test bactericide are the same. The standard methods offer no value for n.

All these difficulties can be avoided if the rate of death is followed in both phenol and test bactericide, by viable counts. Two methods of interpreting the results are discussed:

(1) The comparison of reaction rates, calculated by the formula 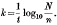This method is complicated by the occurrence of lag period at the start of the reaction between organism and bactericide. This lag period varies in extent in different experiments (often extending up to 50% of the deaths) and makes the interpretation of the results difficult. The lag period has been shown to be a manifestation of, the distribution of logarithmic survival times (Withell, 1942), and is a function of the standard deviation of the logarithmic survivor times (λ). This fact is taken into account in method (2).

(2) The use of the time required for 50% response as a method of comparing bactericides. This time has been symbolized L.t. 50 and is analogous to the lethal dose for the 50% response (l.d. 50) widely used in biological assay. If a logarithmic time scale is used, the logarithmic survival times are found to be approximately normally distributed and consequently probit-logarithm of time lines are straight and in the case of phenol 0·5 % and para-chlor-meta-cresol 0·05% these lines are parallel. In this case a logarithmic time scale means that the comparative times for all percentage responses are equal. In cases where the probit-logarithm-of-time lines are not parallel this would indicate that the standard is unsuitable for the test, for any methods of assay based on a use of a standard to which the organism gives a different response-time relation from that which they give to the test substance or bactericide, are likely to give arbitrary results.

L.T. 50 has been chosen because of the simplicity of the idea underlying it, and because a similar function, L.D. 50, has been used with success in biological assay work. There is also a solid mathematical backing for the use of L.D. 50 in assays involving biological response.

It is suggested that by means of l.t. 50, phenol and the test bactericide can be compared in the following way:

(a) determine the relative speeds of action of the two solutions at any convenient concentrations;

(b) determine the concentration coefficient (ή) of both phenol and test bactericide by means of comparative l.t. 50 values;

(c) determine the temperature coefficient for each substance by similar methods.

From these observations the relative efficiency of the two bactericides can be calculated at any temperature and concentration. If two sets of figures are obtained, one with a vegetative organism, and the other with a sporing organism, a great deal of information can be summarized. It has been shown that an 0·05% solution of parachlor-meta-cresol is approximately one and a half times as efficient as an 0·5% phenol solution (against a Micrococcus). The comparative figure is about 1·0 when Bact. coli is used.

Type
Research Article
Information
Journal of Hygiene , Volume 42 , Issue 4 , July 1942 , pp. 339 - 353
Copyright
Copyright © Cambridge University Press 1942

References

REFERENCES

Bliss, C. I., (1938). The determination of the dosage-mortality curve from small numbers. Quart. J. Pharm. 11, 192.Google Scholar
Bliss, C. I., (1941). Quantitative aspects of biological assay. J. Amer. Pharm. Ass. 29, 465.CrossRefGoogle Scholar
British Standard Specification for determining the Rideal-Walker Coefficient of disinfectants, 1934, no. 541.Google Scholar
British Standard Specification for the modified technique of the Chick-Martin test for disinfectants, 1938, no. 808.Google Scholar
Burn, J. H., (1937). Biological Standardisation. Oxford Medical Publications, pp. 288.Google Scholar
Chick, H., (1908). An investigation of the laws of disinfection. J. Hyg., Camb., 8, 92.CrossRefGoogle ScholarPubMed
Chick, H., (1910). The process of disinfection by chemical agencies and hot water. J. Hyg., Camb., 10, 237.CrossRefGoogle ScholarPubMed
Chick, H., (1912). The factors conditioning the velocity of disinfection. Reprinted from Original communications, 8th International Congress of Applied Chemistry, 26, 167.Google Scholar
Chick, H., (1930). The Theory of Disinfection. A System of Bacteriology in Relation to Medicine. Med. Res. Coun. 1, 179.Google Scholar
Chick, H., & Martin, C. J., (1908). The principles involved in the standardisation of disinfectants and the influence of organic matter on the material value. J. Hyg., Camb., 8, 655.Google Scholar
Gaddum, J. H., (1933). Reports on biological standards. III. Methods of biological assay depending on a quantal response. Spec. Rep. Ser. Med. Res. Coun., Lond., no. 183.Google Scholar
Gaddum, J. H., (1940). Pharmacology. Oxford Medical Publications, pp. 407.Google Scholar
Gladstone, G. P., & Fildes, P., (1940). A simple culture medium for general use without meat extract or peptone. Brit. J. Exp. Path. 21, 161.Google Scholar
Heading, W. R., (1937). Modern chlorinated disinfectants. Pharm. J. 2703.Google Scholar
Henderson Smith, J., (1921). The killing of Botrytis spores by phenol. Ann. App. Biol. 8, 27.Google Scholar
Henderson Smith, J., (1923). The effect of heat on Botrytis spores. Ann. App. Biol. 10, 335.Google Scholar
Klarmann, E., Shternov, V. A., & von Wowerk, J., (1933). The germicidal action of halogen derivatives of phenol and resorcinol and its impairment by organic matter. J. Bact. 17, 423.Google Scholar
Krönig, & Paul, (1897). Die chemische Grundlage der Lehre von der Giftwirkung und Desinfektion. Z. Hyg. InfektKr. 25, 1.Google Scholar
Madsen, & Nyman, (1907). Zur Theorie der-Desinfektion. Z. Hyg. InfektKr. 52, 388.CrossRefGoogle Scholar
Phelps, E. B., (1911). The application of certain laws of physical chemistry in the standardisation of disinfection. J. Infect. Dis. 8, 27.Google Scholar
Rapps, N. F., (1933). The bactericidal efficiency of chlorocresol and chloroxylenol. J. Soc. Chem. Ind., Lond., 52, no. 24, 175 T.Google Scholar
Thaysen, A. C., (1938). Some observations on the R.W. test. J. Hyg., Camb., 38, 558.Google Scholar
Tilley, F. W., (1939). An experimental study of the relation between concentration of disinfectant and time required for disinfection. J. Bact. 38, 499.Google Scholar
Topley, W. W. C., & Wilson, G. S., (1941). The Principles of Bacteriology and Immunity. 2nd edition. Arnold, pp. 1645.Google Scholar
Watson, H. E., (1908). A note on the variation of the rate of disinfection with change in the concentration of disinfectant. J. Hyg., Camb., 8, 536.Google ScholarPubMed
Wilson, G. S., (1922). The proportion of viable bacteria in young cultures, with special reference to the technique employed in counting. J. Bact. 1, 405.Google Scholar
Withell, E. R., (1938). The evaluation of bactericidal action. Quart. J. Pharm. 11, 736.Google Scholar
Withell, E. R., (1942). The significance of the variation in shape of time-survivor curves. J. Hyg., Camb., 42, 124.CrossRefGoogle ScholarPubMed