INTRODUCTION
The enteric commensal bacteria of food animals may act as a reservoir of antimicrobial resistance (AMR) genes, which are often plasmidic [Reference Karczmarczyk1,Reference Salyers, Gupta and Wang2]. Escherichia coli constitutes up to 87% of the culturable Gram-negative faecal bacteria in cattle [Reference Sawant3], and it is proposed as an indicator organism for the extent of resistance of enteric bacteria to antimicrobials [Reference Sharma4]. Resistance of E. coli in cattle in the USA to the cephalosporin ceftiofur has been most often mediated by the plasmidic gene bla CMY-2 [Reference Daniels, Call and Besser5]. Containing resistance to ceftiofur is essential for maintaining veterinary treatment options, as it is the only third-generation cephalosporin licensed for therapeutic use in cattle in the USA. From the public health perspective, if zoonotic transmission may occur, bacteria resistant to ceftiofur are also resistant to cephalosporins used in human medicine [Reference McDermott6]. This is also a well-studied example of predominantly plasmid-mediated AMR in the cattle enteric commensals [Reference Daniels, Call and Besser5]. Both ceftiofur-sensitive and -resistant (bearing bla CMY-2 plasmid) enteric E. coli of cattle are genetically diverse rather than clonal [Reference Daniels, Call and Besser5, Reference Aslam7, Reference Aslam8]. The plasmids are passed vertically during cell divisions [Reference Subbiah9, Reference Poole10], and transferred horizontally via conjugation between bacteria [Reference Daniels, Call and Besser5]. E. coli inhabits not only the enteric but also various non-animate habitats [Reference Savageau11]; the bacterial populations bear the same types of bla CMY-2 plasmids [Reference Mataseje12], and plasmid transfer occurs, albeit at different rates, in the enteric [Reference Licht and Wilcks13] and non-animate habitats [Reference Kruse and Sorum14, Reference Haack and Andrews15]. Other plasmidic genes have recently been recognized as mediators of ceftiofur resistance in E. coli of cattle in the USA [Reference Wittum16].
Some compounds have been proposed for application in food animals to limit AMR spread in their enteric bacteria. In vitro, bambermycin antibiotics modify the plasmid transfer rate among Enterobacteriaceae with the effect's direction (enhanced or reduced rate) dependent on the plasmid [Reference George and Fagerberg17], and reduce net growth of plasmid-bearing bacteria [Reference George and Fagerberg17, Reference Watanabe, Ogata and Sugawara18]. These effects may be sustained in vivo; in-feed bambermycin administration reduces the frequency and degree of AMR in faecal E. coli in cattle [Reference Dealy and Moeller19] and pigs [Reference van den Bogaard20], with little or no decrease in total E. coli numbers [Reference Dealy and Moeller19, Reference van den Bogaard20]. The exact molecular mechanism of action of bambermycins is unknown; it has been hypothesized that pili expressed by plasmid-bearing bacteria attempting to conjugate serve as the drug attachment point [Reference Pfaller21]. Constructed bacteriophages may be another tool for reducing plasmid transfer or killing plasmid-bearing bacteria; that certain phages selectively infect bacteria expressing pili and are thereby able to alter the conjugation rate has been known for some time [Reference Meynell and Lawn22–Reference Novotny, Knight and Brinton25], and is being revisited [Reference Lin26, Reference Lu and Collins27]. Expressing these effects in terms of the parameters of bacterial ecology, bambermycins or phages may be altering the plasmid transfer rate, alone or with killing the plasmid-donor cells, or reducing the rate of replication of the resistant bacteria.
Inducing plasmid loss, termed ‘plasmid curing’ [Reference Trevors28, Reference Spengler29], has been also proposed as an intervention target (see Trevors [Reference Trevors28] for a list of plasmid-curing compounds and procedures). In terms of the bacterial ecology parameters, the effect of plasmid curing is that the resistant cells lose the plasmids and join the pool of antimicrobial-sensitive E. coli at a certain rate.
The size of the realized niche for E. coli among enteric bacteria can be thought of as another intervention target. The niche size may be altered by introducing competitive microflora that are less likely to carry AMR genes (similarly, certain direct-fed microbial strains reduce the number of E. coli O157 in beef cattle faeces [Reference Loneragan and Brashears30]), or by changing the animal's diet [Reference Callaway31]. In non-animate habitats, E. coli numbers may be altered by water sanitation or heat-treatment of the feed. In terms of the bacterial ecology parameters, these interventions would reduce the maximum possible number of E. coli.
Another control option may be offered through exploiting E. coli movement between its animate and non-animate habitats. Although it is generally perceived that enteric bacterial communities are relatively stable, field studies have shown that at the same time E. coli circulates readily between the habitats. A variable fraction of faecal E. coli in beef cattle is composed of strains ingested the day before [Reference Daniels32]. In another experiment, a fed E. coli strain constituted 10–50% of the faecal coliforms for 10 days and a lesser fraction for 4 months post-ingestion, and was recovered in high numbers from the cattle's bedding and drinking water [Reference Marshall, Petrowski and Levy33]. E. coli strains may differ in their propensity to appear in faeces following ingestion [Reference Daniels32, Reference Marshall, Petrowski and Levy33]. Field experiments are yet to address how the partial replacement of enteric E. coli with that ingested and its circulation between the animate and non-animate habitats impact the frequency of AMR. In principle, this parameter of the replacement rate of enteric E. coli may be altered by changing the animal's diet.
In summary, there are several potentially alterable parameters of bacterial ecology that can be targeted by biological interventions to control plasmid-mediated AMR in the cattle enteric commensals. Mathematical modelling is a well-suited method to quantitatively compare the potential efficacy of interventions so that existing intervention approaches can be tailored to, or new approaches can be crafted upon the most promising targets. Here we compared the potential intervention efficacy depending on the targeted parameter in reducing the fraction of resistant enteric E. coli, as an exemplar enteric commensal, in beef cattle by the end of feedlot rearing. We considered interventions within the enteric and non-animate habitats that were targeted to modify the rate of AMR plasmid transfer, the replication rate of resistant E. coli or maximum number of E. coli, to kill the plasmid-donor cells, or to induce plasmid-curing of resistant E. coli. Further, we considered interventions that would change the rate of regular partial replacement of enteric E. coli, or lower maximum E. coli numbers or the frequency of resistant E. coli in animal water or feed supply. Cross-habitat interventions acting similarly on E. coli in water or feed and in the enteric habitat were also considered. Each intervention was delivered consistently throughout the feedlot rearing period.
METHODS
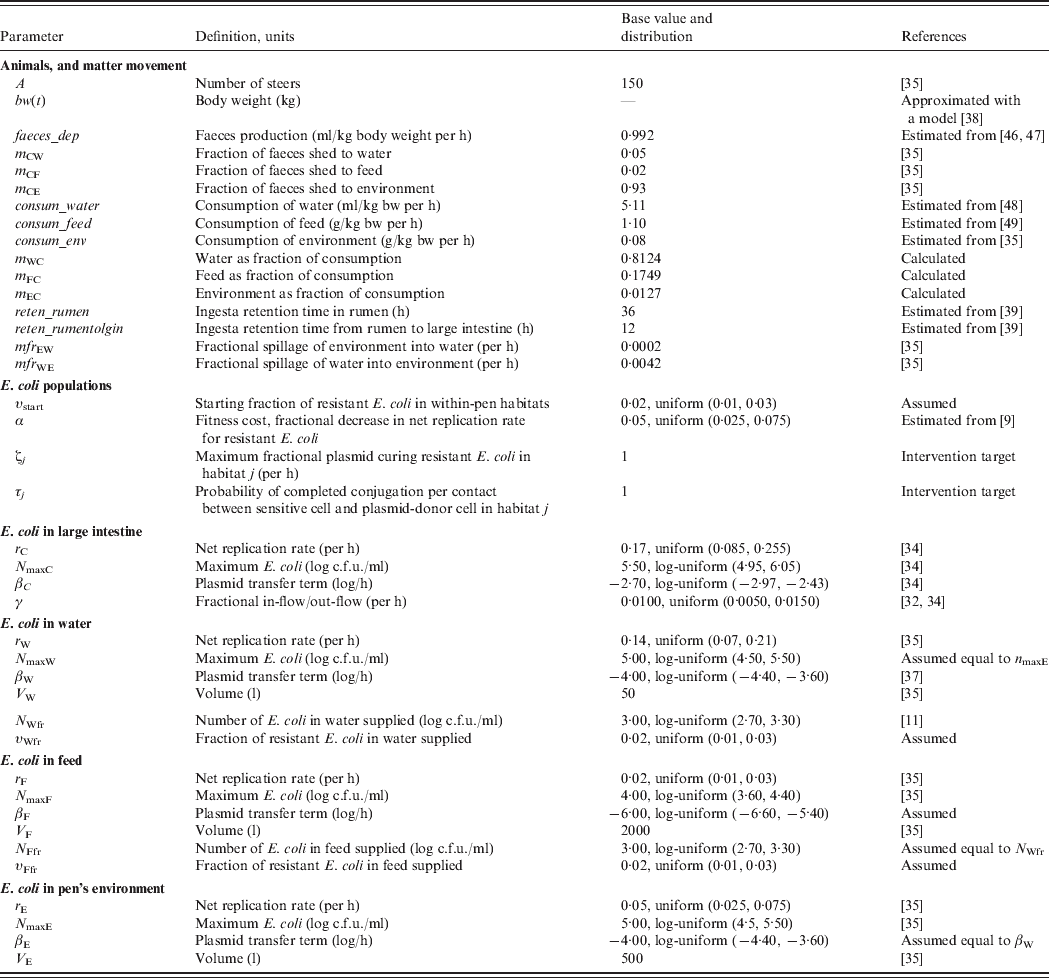
To assess the relative efficacy of the interventions, we developed a deterministic mathematical model of commensal E. coli in a beef feedlot's pen throughout rearing of a group of steers from age 6 to 18 months. For this, we first combined a model of dynamics of ceftiofur-sensitive and -resistant E. coli in the beef cattle large intestine [Reference Volkova, Lanzas, Lu and Grohn34], with a model of the dynamics of E. coli in the pen's non-animate habitats: water in troughs, feed in bunks and the rest of the environment [Reference Ayscue35]. We further developed the resulting model to account for (a) change in the volumes of consumption and faecal deposition by the animals as their body mass grows, (b) E. coli numbers and fractions of resistance in animal water and feed supplies, (c) fractions of resistance in the enteric and pen's non-animate habitats at the start of rearing, (d) retention time of steers' ingesta as it passes through the intestinal tract to the large intestine, and (e) plasmid transfer in E. coli in the non-animate habitats. The model is generally applicable to plasmid-mediated resistance to any antimicrobial. Thereafter, although we use parameter estimates for bla CMY-2 plasmids, we simply refer to plasmid-mediated AMR in commensal E. coli of cattle.
Model assumptions
(1) The habitats of commensal E. coli in a beef feedlot's pen are the large intestines of the cattle, water in troughs, feed in bunks, and the rest of the environment (faecal–soil mix on the floor, other non-animate objects and animal hides). E. coli move between the habitats with substances, e.g. water consumption by cattle or their faecal deposition onto the floor. Transmission of E. coli between the intestines occurs via the other habitats.
(2) In each habitat, population growth of E. coli is density-dependent being restricted by the maximum possible number of E. coli.
(3) E. coli resistance to ceftiofur is plasmid-mediated; AMR plasmids are passed vertically during cell division, and transferred horizontally from resistant to sensitive cells via conjugation.
(4) Bearing AMR plasmid imposes a fitness cost that manifests as a reduction in the net rate of replication of resistant cells compared to sensitive ones [Reference Subbiah9].
(5) There is a continuous fractional replacement of enteric commensal E. coli with equal rates of bacteria out-flow in faeces and in-flow from ingestion [Reference Volkova, Lanzas, Lu and Grohn34].
(6) Steers were not administered ceftiofur therapy or any other compound, e.g. in-feed antimicrobials, neither was any other intervention affecting commensal E. coli delivered to the animals or within the pen's non-animate habitats during the rearing period (except for the targeted interventions modelled).
Model description
In the absence of intervention
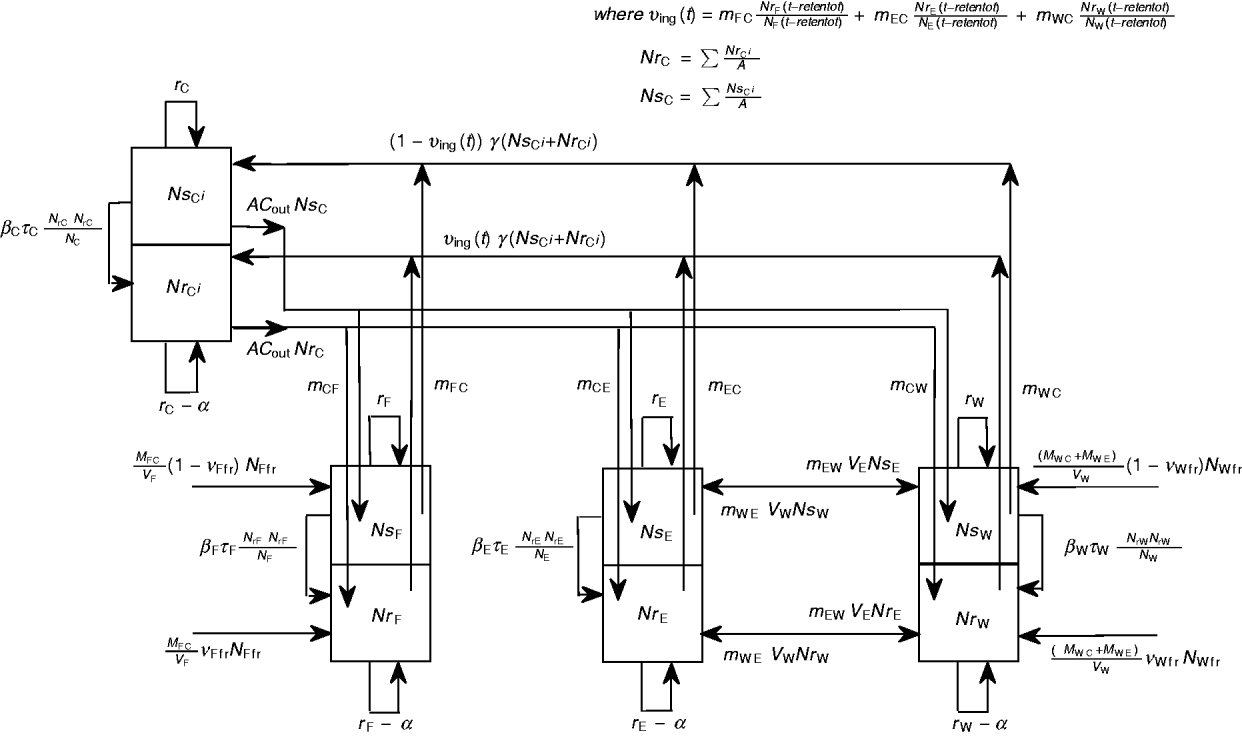
A schematic diagram of the model of commensal E. coli in its habitats within a feedlot's pen is given in Figure 1, and a detailed model diagram scaled per ml of matter is given in Figure 2. For the matter in each habitat, a weight-to-volume ratio of 1 was assumed. Because the focus was bacterial ecology, the unit of time for model parameterization was 1 hour.
Fig. 1 [colour online]. Schematic diagram of the model of commensal E. coli in the within-pen habitats. C, Enteric; W, water in troughs; F, feed in bunks; E, the rest of the environment. S, R, the number of sensitive (S) and resistant (R) E. coli. The arrows show bacterial flows with green for those related to ingesta, yellow for those related to faeces, and black for all others including bacterial population growth and the flow of sensitive cells becoming resistant upon acquisition of plasmids carrying genes of antimicrobial resistance.
Fig. 2. Detailed diagram and parameters of the model of commensal E. coli in within-pen habitats scaled per ml of matter. The parameters are defined in Table 1.
Definitions and values of parameters for the animals and bacterial ecology are given in Table 1. Let A denote the number of steers in the pen. Body weight (bw) of a steer at a given time is bw(t). Volume of faeces deposited by an animal per kg of bw per unit time was faeces_dep, with total volume of faeces deposited C out=bw(t)*faeces_dep. All animals deposited C out*A volume of faeces per unit time, of which fraction m Cj was deposited into non-animate habitat j.
Table 1. Definitions and values of parameters for the animals and bacterial ecology. The model was simulated for a 12-month feedlot rearing period.
Volume of water consumed by an animal from the troughs per kg of bw per unit time was consum_water, of feed consumed from the bunks was consum_feed, and of the pen's environment was consum_env, with total volume of consumption C in=bw(t)* consum_water+bw(t)*consum_feed+bw(t)*consum_env. Fraction of C in coming from non-animate habitat j was denoted mj C (e.g. m wc=consum_water*bw(t)/C in). Hence, total volumes of matter moving between the enteric and non-animate habitats at a given time, t, were:
Faecal contamination of water: M CW=AC outm CW.
Faecal contamination of feed: M CF=AC outm CF.
Faecal contamination of environment: M CE=AC outm CE.
Water consumption by cattle: M WC=AC inm WC.
Feed consumption by cattle: M FC=AC inm FC.
Ingestion of environment by cattle: M EC=AC inm EC.
Volume of non-animate habitat j was Vj. For matter movement between the non-animate habitats per unit time, mfrjk was fractional spillage of j into k, with Mjk the total volume of matter spilled. Total volumes of matter moving between the non-animate habitats at a given time were:
Contamination of water by environment: M EW=V Emfr EW.
Water spillage into environment: M WE=V Wmfr WE.
In habitat j, Nsj was number of antimicrobial sensitive, Nrj the number resistant, and Nj the total number of E. coli/ml. The net rate of E. coli replication was rj; the density-dependent population growth was restricted by the maximum possible number of E. coli/ml, N maxj. Fitness cost to E. coli bearing AMR plasmid was a fractional reduction α in rj. The frequency-dependent [Reference Begon36] plasmid transfer rate from resistant to sensitive E. coli was βjτj(NrjNsj/Nj) per unit time, where the plasmid transfer term βj can be thought of as the rate of contact of sensitive cells with resistant cells attempting to conjugate and τj as probability of completed conjugation per contact [in the absence of intervention, τj = 1 and ‘force of transfer’ per sensitive cell per unit time = βj(Nrj/Nj)].
For animal water and feed supplies, N Wfr and N Ffr denoted total number of E. coli/ml, and υWfr and υFfr fractions of resistant E. coli, respectively.
The ordinary differential equations (1)–(6) describe the change in Nsj and Nrj at a given time in the pen's non-animate habitats in the absence of intervention:
Water in troughs
$$\eqalign{ {{{\rm d}Ns_{\rm W} } \over {{\rm d}t}} \equals \tab r_{\rm W} \left( {1 \minus {{N_{\rm W} } \over {N_{{\rm maxW}} }}} \right)Ns_{\rm W} \minus \beta _{\rm W} \tau _{\rm W} {{Nr_{\rm W} Ns_{\rm W} } \over {N_{\rm W} }} \plus {{M_{{\rm CW}} Ns_{\rm C} \plus M_{{\rm EW}} Ns_{\rm E} \minus M_{{\rm WC}} Ns_{\rm W} \minus M_{{\rm WE}} Ns_{\rm W} } \over {V_{\rm W} }} \cr \tab \plus \left( {{{M_{{\rm WC}} \plus M_{{\rm WE}} } \over {V_{\rm W} }}} \right){\rm \lpar }1 \minus \upsilon _{{\rm Wfr}} \rpar N_{{\rm Wfr}} {\rm \comma } \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{\rm W} } \over {dt}} \equals \tab r_{\rm W} {\rm \lpar }1 \minus \alpha {\rm \rpar }\left( {1 \minus {{N_{\rm W} } \over {N_{{\rm maxW}} }}} \right)Nr_{\rm W} \plus \beta _{\rm W} \tau _{\rm W} {{Nr_{\rm W} Ns_{\rm W} } \over {N_{\rm W} }} \plus {{M_{{\rm CW}} Nr_{\rm C} \plus M_{\rm EW} Nr_{\rm E} \minus M_{{\rm WC}} Nr_{\rm W} \minus M_{{\rm WE}} Nr_{\rm W} } \over {V_{\rm W} }} \cr \tab \plus \left( {{{M_{{\rm WC}} \plus M_{{\rm WE}} } \over {V_{\rm W} }}} \right)\upsilon _{{\rm Wfr}} N_{{\rm Wfr}} . \cr}\hfill$$Feed in bunks
$${{{\rm d}Ns_{\rm F} } \over {{\rm d}t}} \equals r_{\rm F} \left( {1 \minus {{N_{\rm F} } \over {N_{{\rm maxF}} }}} \right)Ns_{\rm F} \minus \beta _{\rm F} \tau _{\rm F} {{Nr_{\rm F} Ns_{\rm F} } \over {N_{\rm F} }} \plus {{M_{{\rm CF}} Ns_{\rm C} \minus M_{{\rm FC}} Ns_{\rm F} } \over {V_{\rm F} }} \plus {{M_{{\rm FC}} } \over {V_{\rm F} }}{\rm \lpar }1 \minus \upsilon _{{\rm Ffr}} {\rm \rpar }N_{{\rm Ffr}} {\rm \comma }\hfill$$
$${{{\rm d}Nr_{\rm F} } \over {{\rm d}t}} \equals r_{\rm F} {\rm \lpar }1 \minus \alpha {\rm \rpar }\left( {1 \minus {{N_{\rm F} } \over {N_{{\rm maxF}} }}} \right)Nr_{\rm F} \plus \beta _{\rm F} \tau _{\rm F} {{Nr_{\rm F} Ns_{\rm F} } \over {N_{\rm F} }} \plus {{M_{{\rm CF}} Nr_{\rm C} \minus M_{{\rm FC}} Nr_{\rm F} } \over {V_{\rm F} }} \plus {{M_{{\rm FC}} } \over {V_{\rm F} }}\upsilon _{{\rm Ffr}} N_{{\rm Ffr}} .\hfill$$Environment
$${{{\rm d}Ns_{\rm E} } \over {{\rm d}t}} \equals r_{\rm E} \left( {1 \minus {{N_{\rm E} } \over {N_{{\rm maxE}} }}} \right)Ns_{\rm E} \minus \beta _{\rm E} \tau _{\rm E} {{Nr_{\rm E} Ns_{\rm E} } \over {N_{\rm E} }} \plus {{M_{{\rm CE}} Ns_{\rm C} \plus M_{{\rm WE}} Ns_{\rm W} \minus M_{{\rm EC}} Ns_{\rm E} \minus M_{{\rm EW}} Ns_{\rm E} } \over {V_{\rm E} }}{\rm \comma }\hfill$$
$${{{\rm d}Nr_{\rm E} } \over {{\rm d}t}} \equals r_{\rm E} \left( {1 \minus \alpha } \right)\left( {1 \minus {{N_{\rm E} } \over {N_{{\rm maxE}} }}} \right)Nr_{\rm E} \plus \beta _{\rm E} \tau _{\rm E} {{Nr_{\rm E} Ns_{\rm E} } \over {N_{\rm E} }} \plus {{M_{{\rm CE}} Nr_{\rm C} \plus M_{{\rm WE}} Nr_{\rm W} \minus M_{{\rm EC}} Nr_{\rm E} \minus M_{{\rm EW}} Nr_{\rm E} } \over {V_{\rm E} }}.\hfill$$In the large intestine, E. coli in-flow and out-flow were at equal fractional rates, γ [Reference Volkova, Lanzas, Lu and Grohn34]. Of in-flowing E. coli, a fraction υing(t) was resistant, being equal to that in E. coli ingested reten_tot hours earlier. The reten_tot was the sum of durations of ingesta retention in the rumen, reten_rumen, and between the rumen and large intestine, reten_rumentolgin. While t, the steer's time in the feedlot, was 0<t⩽reten_tot, the fraction of resistant enteric E. coli in in-flow, υing(t), was equal to that in ingesta consumed by animals prior to their arrival at the feedlot; the latter was assumed to be constant and equal to υstart. The ordinary differential equations (7) and (8) describe the change in NsCi and NrCi at a given time in faecal masses in the large intestine of steer i in the absence of intervention while 0<t⩽reten_tot:
$${{{\rm d}Ns_{{\rm C}^{i} } } \over {{\rm d}t}} \equals r_{\rm C} \left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} }}} \right)Ns_{\rm C} \minus \beta _{\rm C} \tau _{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus \lpar 1 \minus \upsilon _{{\rm start}} \rpar \gamma \lpar Ns_{\rm C} \plus Nr_{\rm C} \rpar \minus \gamma Ns_{\rm C} {\rm \comma }\hfill$$
$${{{\rm d}Nr_{{\rm C}^{i} } } \over {{\rm d}t}} \equals r_{\rm C} {\rm \lpar }1 \minus \alpha {\rm \rpar }\left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} }}} \right)Nr_{\rm C} \plus \beta _{\rm C} \tau _{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus \upsilon _{{\rm start}} \gamma \lpar Ns_{\rm C} \plus Nr_{\rm C} \rpar \minus \gamma Nr_{\rm C} .\hfill$$Equation (9) describes υing(t) when t > reten_tot:
$$v_{{\rm ing}} \lpar t\rpar \equals m_{{\rm WC}} \left( {{{N_{{\rm rW}} \lpar t \minus reten\_tot\rpar } \over {N_{\rm W} \lpar t \minus reten\_tot\rpar }}} \right) \plus m_{{\rm FC}} \left( {{{N_{{\rm rF}} {\rm \lpar }t \minus reten\_tot{\rm \rpar }} \over {N_{\rm F} {\rm \lpar }t \minus reten\_tot{\rm \rpar }}}} \right) \plus m_{{\rm EC}} \left( {{{N_{{\rm rE}} {\rm \lpar }t \minus reten\_tot{\rm \rpar }} \over {N_{\rm E} {\rm \lpar }t \minus reten\_tot{\rm \rpar }}}} \right).\hfill$$The delay differential equations (10) and (11) describe the change in NrCi and NrCi at a given time in faecal masses in the large intestine of steer i in the absence of intervention when t > reten_tot:
$${{{\rm d}Ns_{{\rm C}^{i} } } \over {{\rm d}t}} \equals r_{\rm C} \left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} }}} \right)Ns_{\rm C} \minus \beta _{\rm C} \tau _{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus \lpar 1 \minus \upsilon _{{\rm ing}} {\rm \lpar }t{\rm \rpar }\rpar \gamma \lpar Ns_{\rm C} \plus Nr_{\rm C} \rpar \minus \gamma Ns_{\rm C} {\rm \comma }\hfill$$
$${ {{{\rm d}Nr_{{\rm C}^{i} } } \over {{\rm d}t}} \equals r_{\rm C} \lpar 1 \minus \alpha \rpar \left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} }}} \right)Nr_{\rm C} \plus \beta _{\rm C} \tau _{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus \upsilon _{{\rm ing}} {\rm \lpar }t{\rm \rpar }\gamma {\rm \lpar }Ns_{\rm C} \plus Nr_{\rm C} {\rm \rpar } \minus \gamma Nr_{\rm C} . }\hfill $$The values of variables Nr W, N W, Nr F, N F, Nr E and N E from the solutions of equations (1)–(6), while 0<t⩽reten_tot were used as the initial values to calculate υing(t) for equations (10) and (11).
As each animal contributed the same amount C out to the total faecal deposits, the number of antimicrobial-sensitive E. coli/ml of the deposits was 
$Ns_{\rm C} \equals \mathop{\sum\limit^{A}_{i \equals \setnum{1}} Ns_{{\rm C}^{i} } } \sol A$ and the number of resistant E. coli was 
$Nr_{\rm C} \equals \mathop{\sum^{A}_{i \equals \setnum{1}} Nr_{{\rm C}^{i} } } \sol A$.
In the presence of intervention
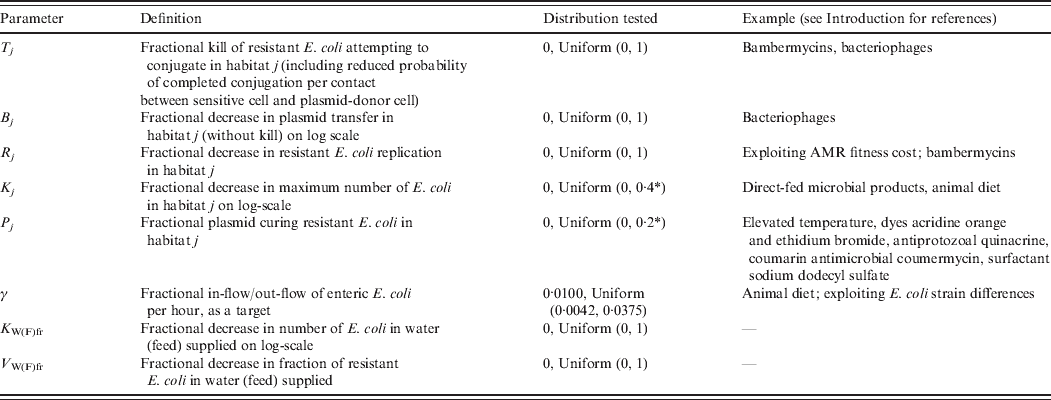
Definitions and values of parameters reflecting the targeted effects of interventions are given in Table 2. For an intervention in habitat j, Rj denotes fractional reduction in net rate of replication of resistant E. coli. Tj denotes fractional reduction in probability of completed conjugation per contact between sensitive cell and plasmid-donor cell due to death of the latter, and Bj is the fractional reduction in the plasmid transfer rate via any other mechanism. Kj is the fractional reduction in maximum number of E. coli. Pj is the fractional rate of plasmid-curing resistant E. coli (the sensitized cells did not differ from the originally sensitive cells in replication rate or propensity to receive plasmids), with ζj the maximum rate of 1 per hour. The change in rates of fractional in-flow and out-flow of enteric E. coli was modelled by varying the corresponding parameter, γ [Reference Volkova, Lanzas, Lu and Grohn34]. V Wfr denotes a fractional decrease in υWfr, and V Ffr in υFfr.
Table 2. Definitions and values of parameters representing targeted effects of interventions. Examples of existing and potential biological intervention approaches that have been shown, based on empirical data for E. coli in vitro or enteric E. coli in vivo, or are hypothesized to produce such effects
AMR, Antimicrobial resistance.
aFurther increasing the parameter value for an intervention in the enteric habitat did not lead to a further reduction in the number of resistant enteric E. coli.
The ordinary differential equations (12)–(17) describe the change in Ns j and Nr j at a given time in the pen's non-animate habitats in the presence of intervention:
Water in troughs
$$\eqalign{ {{{\rm d}Ns_{\rm W} } \over {{\rm d}t}} \equals \tab r_{\rm W} \left( {1 \minus {{N_{\rm W} } \over {N_{{\rm maxW}} {\rm \lpar }1 \minus K_{\rm w} {\rm \rpar }}}} \right)Ns_{\rm W} \minus \beta _{\rm W} {\rm \lpar }1 \minus B_{\rm W} {\rm \rpar }\tau _{\rm W} {\rm \lpar }1 \minus T_{\rm W} {\rm \rpar }{{Nr_{\rm W} Ns_{\rm W} } \over {N_{\rm W} }} \plus P_{\rm W} \zeta _{\rm W} Nr_{\rm W} \cr \tab \vskip 12pt\plus {{M_{{\rm CW}} Ns_{\rm C} \plus M_{{\rm EW}} Ns_{\rm E} \minus M_{{\rm WC}} Ns_{\rm W} \minus M_{{\rm WE}} Ns_{\rm W} } \over {V_{\rm W} }} \cr \tab \plus \left( {{{M_{{\rm WC}} \plus M_{{\rm WE}} } \over {V_{\rm W} }}} \right){\rm \lpar }1 \minus \upsilon _{{\rm Wfr}} {\rm \lpar }1 \minus V_{{\rm Wfr}} {\rm \rpar \rpar }N_{{\rm Wfr}} {\rm \lpar }1 \minus K_{{\rm Wfr}} {\rm \rpar \comma } \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{\rm W} } \over {{\rm d}t}} \equals \tab r_{\rm W} \left( {1 \minus \alpha } \right)\left( {1 \minus R_{\rm W} } \right)\left( {1 \minus {{N_{\rm W} } \over {N_{{\rm maxW}} {\rm \lpar }1 \minus K_{w} {\rm \rpar }}}} \right)Nr_{\rm W} \plus \beta _{\rm W} {\rm \lpar }1 \minus B_{\rm W} {\rm \rpar }\tau _{\rm W} {\rm \lpar }1 \minus T_{\rm W} {\rm \rpar }{{Nr_{\rm W} Ns_{\rm W} } \over {N_{\rm W} }} \cr \tab \vskip 8pt\minus \beta _{\rm W} {\rm \lpar }1 \minus B_{\rm W} {\rm \rpar }\tau _{\rm W} T_{\rm W} {{Nr_{\rm W} Ns_{\rm W} } \over {N_{\rm W} }} \minus P_{\rm W} \zeta _{\rm W} Nr_{\rm W} \plus {{M_{{\rm CW}} Nr_{\rm C} \plus M_{{\rm EW}} Nr_{\rm E} \minus M_{{\rm WC}} Nr_{\rm W} \minus M_{{\rm W}{\rm E}} Nr_{\rm W} } \over {V_{\rm W} }} \cr \tab \vskip 8pt\plus \left( {{{M_{{\rm WC}} \plus M_{{\rm WE}} } \over {V_{\rm W} }}} \right)\upsilon _{{\rm Wfr}} {\rm \lpar }1 \minus V_{{\rm Wfr}} {\rm \rpar }N_{{\rm Wfr}} {\rm \lpar }1 \minus K_{{\rm Wfr}} {\rm \rpar }{\rm .} \cr}\hfill $$Feed in bunks
$$\eqalign{ {{{\rm d}Ns_{\rm F} } \over {{\rm d}t}} \equals \tab r_{\rm F} \left( {1 \minus {{N_{\rm F} } \over {N_{{\rm maxF}} {\rm \lpar }1 \minus K_{\rm F} {\rm \rpar }}}} \right)Ns_{\rm F} \minus \beta _{\rm F} {\rm \lpar }1 \minus B_{\rm F} {\rm \rpar }\tau _{\rm F} {\rm \lpar }1 \minus T_{\rm F} {\rm \rpar }{{Nr_{\rm F} Ns_{\rm F} } \over {N_{\rm F} }} \plus P_{\rm F} \zeta _{\rm F} Nr_{\rm F} \cr \tab \plus {{M_{{\rm CF}} Ns_{\rm C} \minus M_{{\rm FC}} Ns_{\rm F} } \over {V_{\rm F} }} \plus {{M_{{\rm FC}} } \over {V_{\rm F} }}{\rm \lpar }1 \minus \upsilon _{{\rm Ffr}} {\rm \lpar }1 \minus V_{{\rm Ffr}} {\rm \rpar \rpar }N_{{\rm Ffr}} {\rm \lpar }1 \minus K_{{\rm Ffr}} {\rm \rpar }\comma \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{\rm F} } \over {{\rm d}t}} \equals \tab r_{\rm F} {\rm \lpar }1 \minus \alpha {\rm \rpar \lpar }1 \minus R_{\rm F} {\rm \rpar }\left( {1 \minus {{N_{\rm F} } \over {N_{{\rm maxF}} {\rm \lpar }1 \minus K_{\rm F} {\rm \rpar }}}} \right)Nr_{\rm F} \plus \beta _{\rm F} {\rm \lpar }1 \minus B_{\rm F} {\rm \rpar }\tau _{\rm F} {\rm \lpar }1 \minus T_{\rm F} {\rm \rpar }{{Nr_{\rm F} Ns_{\rm F} } \over {N_{\rm F} }} \cr \tab \minus \beta _{\rm F} {\rm \lpar }1 \minus B_{\rm F} {\rm \rpar }\tau _{\rm F} T_{\rm F} {{Nr_{\rm F} Ns_{\rm F} } \over {N_{\rm F} }} \minus P_{\rm F} \zeta _{\rm F} Nr_{\rm F} \plus {{M_{{\rm CF}} Nr_{\rm C} \minus M_{{\rm FC}} Nr_{\rm F} } \over {V_{\rm F} }} \cr \tab \plus {{M_{{\rm FC}} } \over {V_{\rm F} }}\upsilon _{{\rm Ffr}} {\rm \lpar }1 \minus V_{{\rm Ffr}} {\rm \rpar }N_{{\rm Ffr}} {\rm \lpar }1 \minus K_{{\rm Ffr}} {\rm \rpar }{\rm .} \cr}\hfill $$Environment
$$\eqalign{ {{{\rm d}Ns_{\rm E} } \over {{\rm d}t}} \equals \tab r_{\rm E} \left( {1 \minus {{N_{\rm E} } \over {N_{{\rm maxE}} {\rm \lpar }1 \minus K_{\rm E} {\rm \rpar }}}} \right)Ns_{\rm E} \minus \beta _{\rm E} {\rm \lpar }1 \minus B_{\rm E} {\rm \rpar }\tau _{\rm E} {\rm \lpar }1 \minus T_{\rm E} {\rm \rpar }{{Nr_{\rm E} Ns_{\rm E} } \over {N_{\rm E} }} \plus P_{\rm E} \rmzeta _{\rm E} Nr_{\rm E} \cr \tab \vskip 8pt\plus {{M_{{\rm CE}} Ns_{\rm C} \plus M_{{\rm WE}} Ns_{\rm W} \minus M_{{\rm EC}} Ns_{\rm E} \minus M_{{\rm EW}} Ns_{\rm E} } \over {V_{\rm E} }}{\rm \comma } \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{\rm E} } \over {{\rm d}t}} \equals \tab r_{\rm E} {\rm \lpar }1 \minus \alpha {\rm \rpar \lpar }1 \minus R_{\rm E} {\rm \rpar }\left( {1 \minus {{N_{\rm E} } \over {N_{{\rm maxE}} {\rm \lpar }1 \minus K_{\rm E} {\rm \rpar }}}} \right)Nr_{\rm E} \plus \beta _{\rm E} {\rm \lpar }1 \minus B_{\rm E} {\rm \rpar }\tau _{\rm E} {\rm \lpar }1 \minus T_{\rm E} {\rm \rpar }{{Nr_{\rm E} Ns_{\rm E} } \over {N_{\rm E} }} \cr \tab \vskip 8pt \minus \beta _{\rm E} {\rm \lpar }1 \minus B_{\rm E} {\rm \rpar }\tau _{\rm E} T_{\rm E} {{Nr_{\rm E} Ns_{\rm E} } \over {N_{\rm E} }} \minus P_{\rm E} \zeta _{\rm E} Nr_{\rm E} \plus {{M_{{\rm CE}} Nr_{\rm C} \plus M_{{\rm WE}} Nr_{\rm W} \minus M_{{\rm EC}} Nr_{\rm E} \minus M_{{\rm EW}} Nr_{\rm E} } \over {V_{\rm E} }}. \cr}\hfill $$The ordinary differential equations (18) and (19) describe the change in NrCi and NrCi at a given time in faecal masses in the large intestine of steer i in the presence of intervention while 0<t⩽reten_tot:
$$\eqalign{ {{{\rm d}Ns_{C^{i} } } \over {{\rm d}t}} \equals \tab r_{\rm C} \left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} {\rm \lpar }1 \minus K_{\rm C} {\rm \rpar }}}} \right)Ns_{\rm C} \minus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\tau _{\rm C} {\rm \lpar }1 \minus T_{\rm C} {\rm \rpar }{{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus P_{\rm C} \zeta _{\rm C} Nr_{\rm C} \cr \tab \plus {\rm \lpar }1 \minus \upsilon _{{\rm start}} {\rm \rpar }\gamma \lpar Ns_{\rm C} \plus Nr_{\rm C} \rpar \minus \gamma Ns_{\rm C} {\rm \comma } \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{{\rm C}^{i} } } \over {{\rm d}t}} \equals \tab r_{\rm C} {\rm \lpar }1 \minus \alpha {\rm \rpar \lpar }1 \minus R_{\rm C} {\rm \rpar }\left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} {\rm \lpar }1 \minus K_{\rm C} {\rm \rpar }}}} \right)Nr_{\rm C} \plus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\rmtau _{\rm C} {\rm \lpar }1 \minus T_{\rm C} \rpar {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \cr \tab \vskip 10pt\minus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\tau _{\rm C} T_{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \minus P_{\rm C} \zeta _{\rm C} Nr_{\rm C} \plus \upsilon _{{\rm start}} \rmgamma {\rm \lpar }Ns_{\rm C} \plus Nr_{\rm C} {\rm \rpar } \minus \rmgamma Nr_{\rm C} . \cr}\hfill $$The delay differential equations (20) and (21) describe the change in NrCi and NrCi at a given time in faecal masses in the large intestine of steer i in the presence of intervention when t > reten_tot[the values of variables Nr W, N W, Nr F, N F, Nr E and N E from the solutions of equations (12)–(17) while 0<t⩽reten_tot were used as the initial values to calculate υing(t) for equations (20) and (21)]
$$\eqalign{ {{{\rm d}Ns_{{\rm C}^{i} } } \over {{\rm d}t}} \equals \tab r_{\rm C} \left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} {\rm \lpar }1 \minus K_{\rm C} {\rm \rpar }}}} \right)Ns_{\rm C} \minus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\tau _{\rm C} {\rm \lpar }1 \minus T_{\rm C} {\rm \rpar }{{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \plus P_{\rm C} \zeta _{\rm C} Nr_{\rm C} \cr \tab \plus {\rm \lpar }1 \minus \upsilon _{{\rm ing}} {\rm \lpar }t{\rm \rpar \rpar }\gamma {\rm \lpar }Ns_{\rm C} \plus Nr_{\rm C} {\rm \rpar } \minus \gamma Ns_{\rm C} {\rm \comma } \cr}\hfill $$
$$\eqalign{ {{{\rm d}Nr_{{\rm C}^{i} } } \over {{\rm d}t}} \equals \tab r_{\rm C} {\rm \lpar }1 \minus \alpha {\rm \rpar \lpar }1 \minus R_{\rm C} {\rm \rpar }\left( {1 \minus {{N_{\rm C} } \over {N_{{\rm maxC}} {\rm \lpar }1 \minus K_{\rm C} {\rm \rpar }}}} \right)Nr_{\rm C} \plus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\tau _{\rm C} {\rm \lpar }1 \minus T_{\rm C} {\rm \rpar }{{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \cr \tab \vskip 8pt\minus \beta _{\rm C} {\rm \lpar }1 \minus B_{\rm C} {\rm \rpar }\tau _{\rm C} T_{\rm C} {{Nr_{\rm C} Ns_{\rm C} } \over {N_{\rm C} }} \minus P_{\rm C} \zeta _{\rm C} Nr_{\rm C} \plus \upsilon _{{\rm ing}} {\rm \lpar }t{\rm \rpar }\gamma {\rm \lpar }Ns_{\rm C} \plus Nr_{\rm C} {\rm \rpar } \minus \gamma Nr_{\rm C} . \cr}\hfill $$Model parameterization
The base parameter values were adopted or estimated from the published literature (Table 1) with the following exceptions. The number of E. coli in animal feed supply was taken to be equal to a value reported in the literature for watersheds of grazed cattle pastures and feedlots [Reference Savageau11]. The plasmid transfer term (thought of as the rate of contact of sensitive cells with resistant cells attempting to conjugate) in E. coli in the pen's environment was taken to be equal to a reported value for water [Reference Cernat37]. A lower term was assumed for transfer in feed, because of a likely larger degree of separation of bacteria in this matrix.
Steer body weight, bw(t), was approximated with a published model of body weight of male beef cattle by day of rearing [Reference Hassen38]. The durations of ingesta retention in the rumen, and between the rumen and large intestine, were estimated as the averages of those reported in beef steers for high-concentrate grain-based diets [Reference Martin, Philippeau and Michalet-Doreau39].
Low fractions of E. coli with bla CMY-2 plasmids are present on cattle farms even in the absence of ceftiofur use [Reference Daniels32, Reference Morley40]. The plasmidic genes coding for cephalosporin resistance are also present in E. coli in surface and drinking water [Reference Mataseje41–Reference Hamelin43]. Reflecting these field data, model simulations were started, at the time of steer placement into the pen, with a base 2·0% fraction of resistant E. coli in all four within-pen habitats, υstart, as well as in fresh water, υWfr, and feed, υFfr, supplies. The model was simulated with 150 steers reared in the pen for 360 days from age 6 to 18 months.
Model solutions and analysis
Solutions of model equations were approximated numerically using the embedded fourth-order Runge–Kutta method implemented in Vensim® PLE Plus software (Ventana Systems Inc., USA). The model analysis included three steps:
Step 1. Sensitivity of the fraction of resistant enteric E. coli and of the fraction of resistant E. coli in steers' ingesta by slaughter age (by the end of 12-month feedlot rearing) to variability in parameter values of bacterial ecology (Table 1, parameters of E. coli populations) in the absence of intervention was evaluated. For this, 200 model simulations were performed with the parameter values obtained by Latin hypercube sampling [Reference McKay, Beckman and Conover44]. Due to a paucity of empirical data on the parameters' distributions, each was assumed to follow a uniform (with boundaries at ±50% of the base value) or a log-uniform (with boundaries at ±10% of the base value on log-scale) distribution (Table 1). With the simulation output, a multiple linear regression model with standardized regression coefficients was built for each outcome as the dependent variable and the parameters as candidate predictors. The regression models were built in SAS® v. 9·1 software for Windows (SAS Institute Inc., USA), and used partial type III sum of squares to test the significance of association between the predictor values and dependent variable given the effects of the other predictors. Backward elimination was the predictor selection routine with the 0·05 significance level to stay in the model. Additionally, sensitivity of the final fractions of resistance to the starting fraction, υstart (in the range 0·00001–0·5), was investigated.
Step 2. Intervention parameters Rj, Kj, Bj, Tj, Pj, V Wfr or V Wfr were introduced into the mathematical model one at a time, and taken to follow a uniform (0, 1) (except for Kj and Pj; see Table 2). In another simulation, parameter γ was sampled with the boundaries corresponding to a 10% and 90% daily replacement of enteric E. coli (Table 1). Cross-habitat interventions, acting on the same parameter in E. coli in water in troughs or feed in bunks and in the intestines, were also simulated. When simulating each intervention, the rest of the parameters' distributions were set and 100 model simulations performed as in step 1. With the simulation output, for each intervention parameter and each of the two outcome resistance fractions: (a) relationships were explored graphically; (b) correlation, given outcome variability introduced by the other parameters of bacterial ecology, was estimated with Spearman's correlation coefficient (ρ) and considered significant if P ⩽ 0·05; and (c) a multiple linear regression model was built as in step 1 to check that the intervention was significantly associated (P ⩽ 0·05) with the outcome after accounting for the effects of the other parameters of bacterial ecology.
Step 3. For each significant intervention target identified in step 2, uncertainty in the effects on the outcome given variability introduced by the other parameters of bacterial ecology was explored graphically with a box-and-whisker plot. The data for each value of the intervention parameter were obtained with the rest of the parameters' distributions set and 100 model simulations performed as in step 1. Figures were made in SigmaPlot™ (Systat Software Inc., USA).
RESULTS
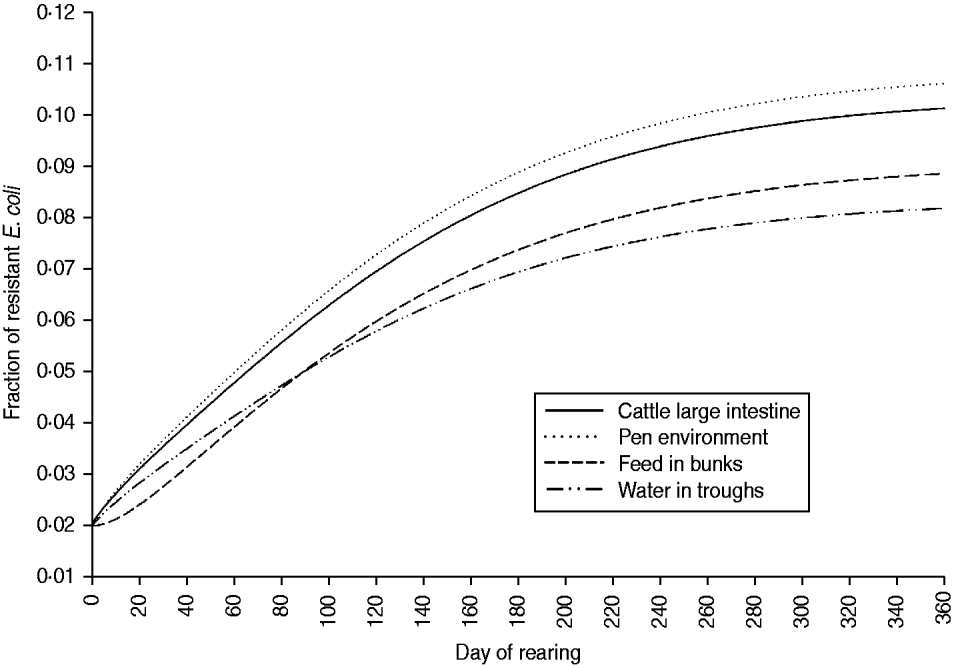
Fraction of resistant E. coli in the absence of intervention
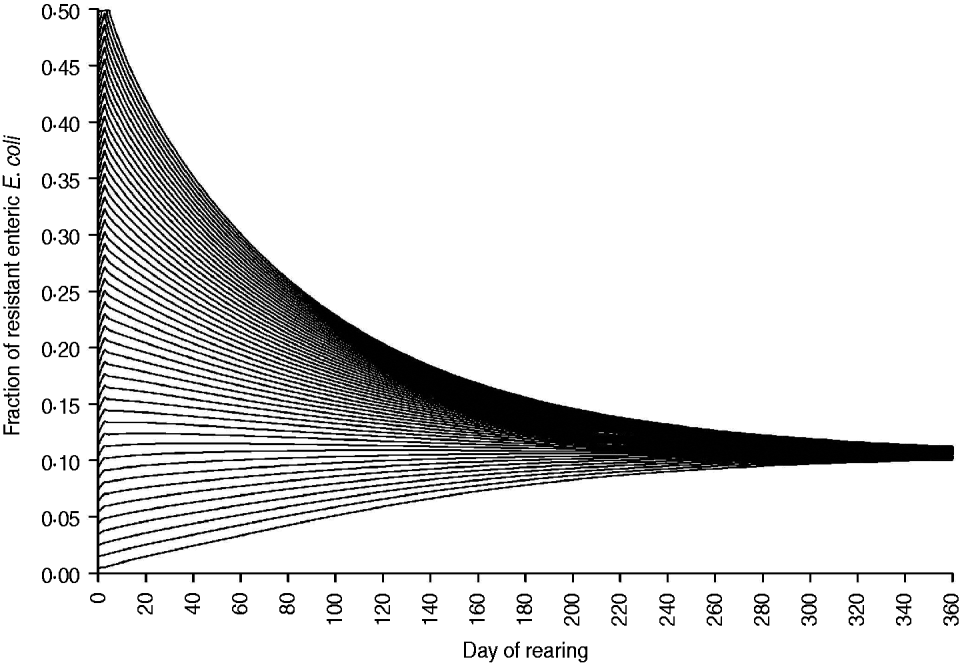
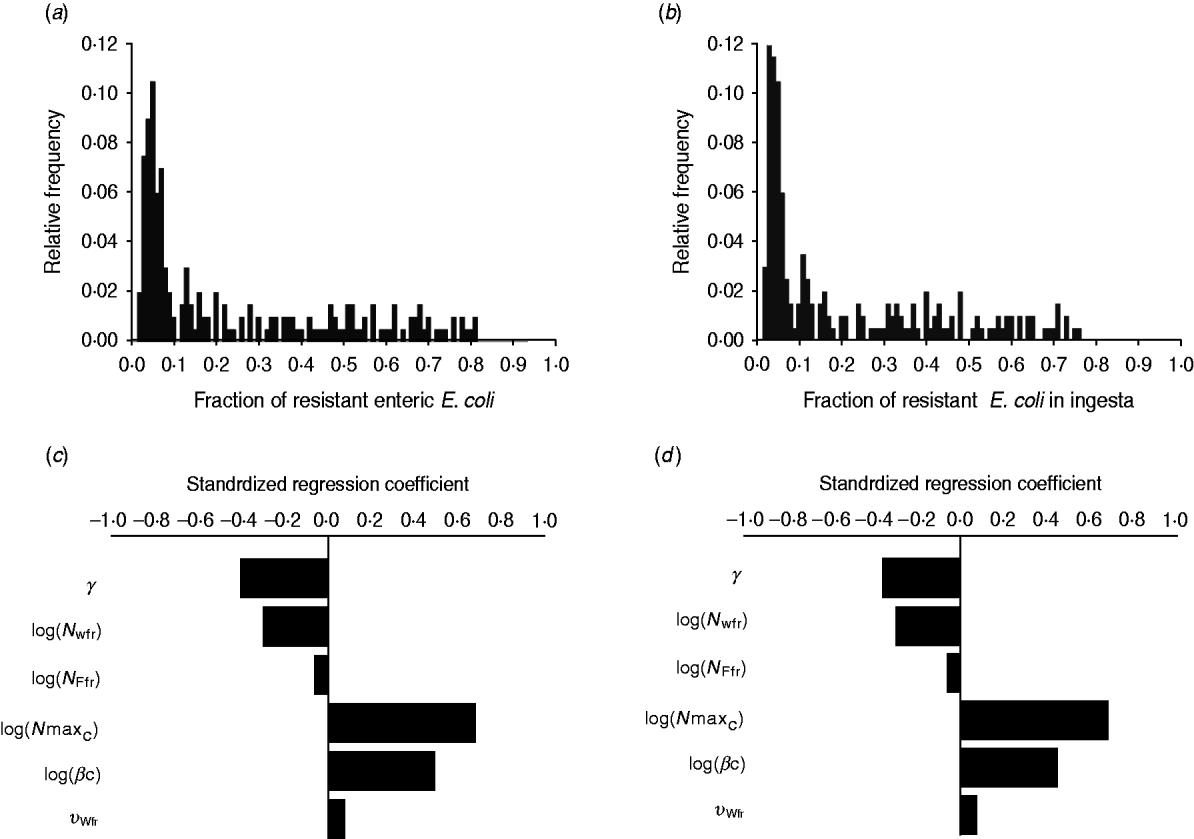
The fraction of resistant enteric E. coli by the end of feedlot rearing did not depend on the starting fraction (Fig. 3), as long as at least some AMR-plasmid-bearing E. coli (e.g. 0·001% of total cells) were present at the start. Equilibrium of the fraction of resistant E. coli was reached in a 12-month rearing period; this was independent of the starting fraction of resistance (Fig. 3). In the base scenario with 2% of resistant E. coli at the start, the fractions of resistance in all the habitats steadily rose throughout the rearing period (Fig. 4). Beyond the 5th day of rearing, the fraction of resistant E. coli in the pen's environment was slightly higher than that in enteric E. coli, where it rose from 2·0% at steer placement to 10·1% at slaughter age (Fig. 4). In terms of uncertainty in the outcome in the absence of intervention, of 200 model simulations, 48% produced the final fraction of resistant enteric E. coli of ⩽0·10, with a wide distribution of the outcome across the other half of simulations (Fig. 5 a). This outcome was positively associated with rate of plasmid transfer and maximum possible E. coli numbers in the enteric habitat, and less so with fraction of resistant E. coli in the water supplied (Fig. 5 c). The outcome was negatively associated with rate of replacement of enteric E. coli and E. coli numbers in fresh water and, to a lesser extent, feed supplies (Fig. 5 c). The final fraction of resistant enteric E. coli was not highly sensitive to the total ingesta retention time prior to the large intestine, varying between 10 and 100 hours (data not shown).
Fig. 3. Fraction of resistant enteric E. coli throughout the 12-month feedlot rearing period depending on the starting value.
Fig. 4. Model solutions with base parameter values. Fractions of resistant commensal E. coli in the within-pen habitats throughout the 12-month feedlot rearing period.
Fig. 5. Uncertainty in and sensitivity of the outcomes to variation in the parameters of bacterial ecology in the absence of intervention. Uncertainty: fraction of resistant (a) enteric E. coli or (b) E. coli in ingesta by the end of feedlot rearing (over 200 model simulations). Sensitivity: standardized regression coefficients for parameters (P ⩽ 0·05) in the multiple linear regression model where the dependent variable was the fraction of resistant (c) enteric E. coli or (d) E. coli in ingesta by the end of rearing. Parameters: γ, fractional regular replacement rate of enteric E. coli; log(N Wfr), log(N Ffr), log c.f.u. E. coli/ml in fresh water and feed supplied, respectively; log(N maxC), log(βC), maximum log c.f.u. E. coli/ml and the rate of plasmid transfer in the enteric habitat, respectively; υWfr, fraction of resistant E. coli in fresh water supplied.
We then considered if any additional parameters influenced the fraction of resistant E. coli in the steer's ingesta by the end of the feedlot rearing period, given the build-up of resistance in the pen's non-animate habitats (Fig. 4). Uncertainty in this outcome was similar to that in the final fraction of resistant enteric E. coli (Fig. 5 b). The fraction of resistant E. coli in ingesta was also associated with the same parameters of bacterial ecology (Fig. 5 d).
Potential efficacy of interventions
The efficacy of interventions delivered throughout feedlot rearing in reducing the fraction of resistance in enteric E. coli or in E. coli in the steer's ingesta by the end of rearing varied depending on the targeted parameter of bacterial ecology (Fig. 6). Twenty-one interventions targeting a single parameter in a given E. coli habitat, along with four acting on the same parameter in water in troughs and intestines or feed in bunks and intestines, and four acting on E. coli in water or feed supplies were evaluated. Six one-habitat interventions were significantly correlated with a reduction in the final fractions of resistance after accounting for the effects of the other parameters of bacterial ecology. Five of these six acted on enteric E. coli (B C, T C, P C, K C, y); the magnitude of the effects was not sizably enhanced by simultaneous action on E. coli in water or feed (Fig. 6). One potential intervention (K Wfr) was significantly correlated with an increase in the final fractions of resistance (Fig. 6), and is discussed below.
Fig. 6. Ranking intervention targets. Value of Spearman's correlation coefficient (P ⩽ 0·05) between parameter values and fraction of resistant (a) enteric E. coli or (b) E. coli in ingesta by the end of feedlot rearing, given outcome variability introduced by the other parameters of bacterial ecology. For each intervention parameter the data are from 100 model simulations. Parameters: B C, B W, B F, fractional reduction on log scale in plasmid transfer in E. coli in the enteric habitat, water in troughs or feed in bunks, respectively; T C, T W, T F, fractional death of the plasmid-donor cells in E. coli in the enteric habitat, water in troughs or feed in bunks, respectively; γ, fractional regular replacement rate of enteric E. coli; K C, K W, K F, fractional reduction (between 0 and 0·4) in maximum E. coli log c.f.u./ml enteric habitat, water in troughs or feed in bunks, respectively; K Wfr, fractional reduction in E. coli log c.f.u./ml fresh water supplied; P C, P W, P F, P E, fractional plasmid curing (between 0 and 0·2) resistant E. coli in the enteric habitat, water in troughs, feed in bunks or the pen's environment, respectively.
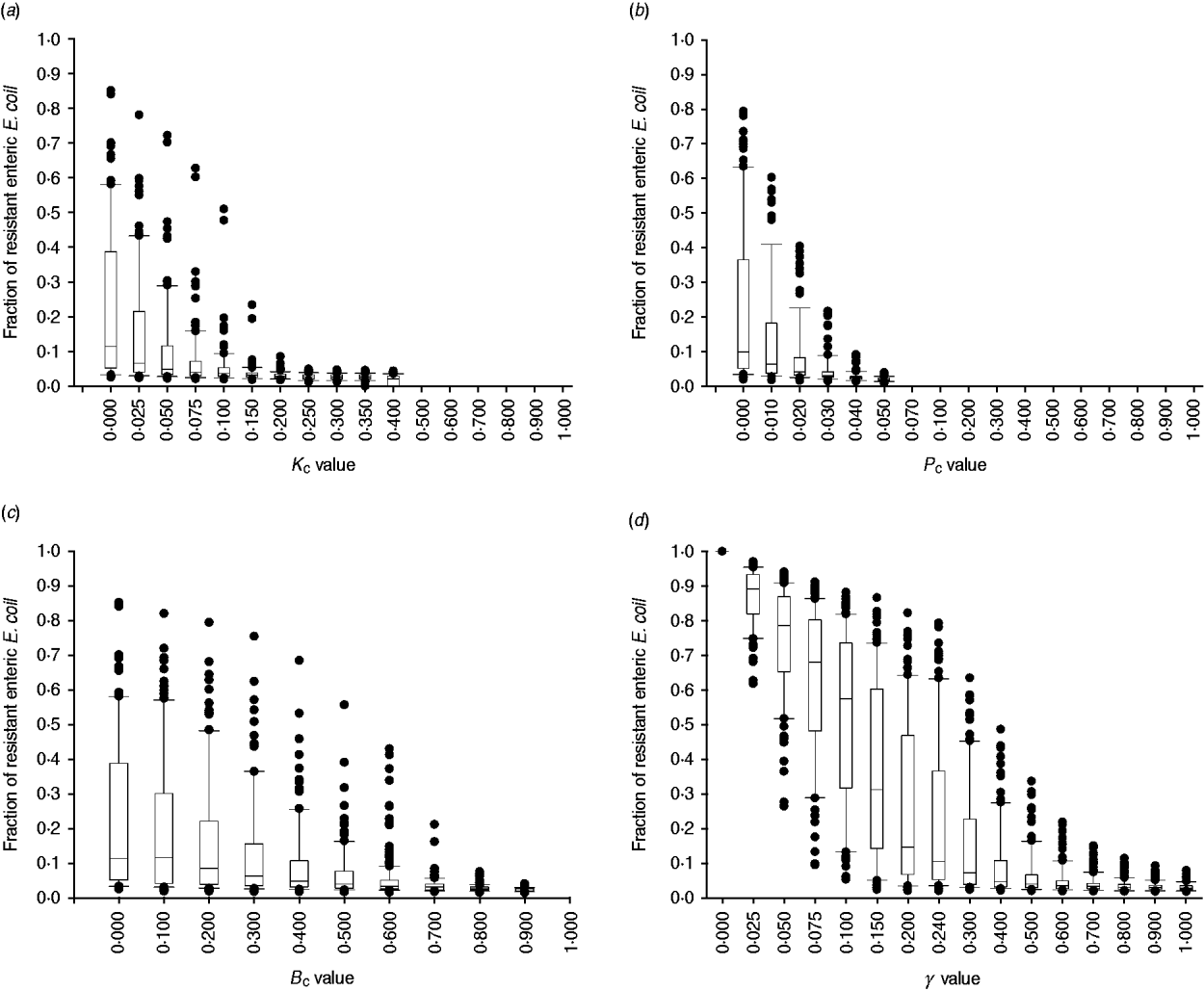
The degree of uncertainty in the effects due to variability in the other parameters of bacterial ecology varied between the interventions (Fig. 7). Highly effective were interventions capable of plasmid-curing enteric E. coli or reducing their maximum number (Fig. 7 a, b). The effects of reducing the rate of plasmid transfer or increasing the rate of replacement of enteric E. coli, although also significant, were more gradual (Fig. 7 c, d).
Fig. 7. Uncertainty in interventions lowering the fraction of resistant enteric E. coli by the end of feedlot rearing due to outcome variability introduced by the other parameters of bacterial ecology. For each value of intervention parameter the data are from 100 model simulations. The box-and-whisker plot is included for each value until the median outcome of 100 simulations ⩽0·02 (starting fraction of resistance). The effects of an intervention that in the enteric habitat (a) reduces maximum E. coli log c.f.u./ml by fraction K C, (b) induces plasmid curing of P C fraction of resistant E. coli, (c) reduces plasmid transfer rate on log scale by fraction B C; or (d) alters fractional daily replacement rate of enteric E. coli, γ.
DISCUSSION
Within-pen ecology of commensal E. coli during the rearing period determined what fraction of steers' enteric E. coli bear AMR plasmids by the end of rearing, as long as AMR plasmids were present at the start. The final fraction of resistance was insensitive to that at steer placement and, in terms of supplies, lightly sensitive to the frequency of resistance in E. coli in fresh water supplied. Values of individual parameters of the within-pen ecology are likely to vary between the feedlots; this was addressed by considering uncertainty in the outcome in the absence (Fig. 5 a, b) and presence (Fig. 7) of intervention. Similarity between the parameters associated with fractions of resistance in enteric E. coli and in E. coli in steers' ingesta (Fig. 5 c, d) showed that circulation of commensal E. coli between the enteric and non-animate habitats within the pen is an important component in determining the final frequencies of resistance across the habitats. In further discussion we simply refer to the final fraction of resistant enteric (faecal) E. coli as a representative within-pen outcome, and because of the significance of faeces as a vehicle of transmission of microbial AMR genes beyond the farm systems.
In the absence of intervention, a higher fraction of resistant enteric E. coli was associated with higher plasmid transfer rate and maximum E. coli number in this habitat, and, to a much lesser extent, with a higher frequency of resistance in the water supplied (Fig. 5 c). The former two were significant because the rate of plasmid transfer in E. coli in faecal masses in the large intestines was the highest of all the habitats. Consequently, an intervention targeted at lowering the number of enteric E. coli throughout rearing was highly efficient (Figs 6, 7 a). Reducing maximum E. coli numbers in the large intestines' faecal masses by 20% on log-scale (from 316 000 to 25 000/ml) led to a marked decrease in the final fraction of resistance; the effect was relatively insensitive to other variations in bacterial ecology (Fig. 7 a). This was because lowering enteric E. coli led to fewer resistant E. coli shed in faeces (K C, varying from 0 to 0·4, and the number of resistant E. coli/ml of the steers' faecal deposits by the end of rearing: ρ = −0·91, P < 0·001). This reduced the plasmid transfer in the non-animate habitats (e.g. K C and the number of sensitive E. coli in water in troughs receiving plasmids per hour: ρ = −0·59, P < 0·001), and so ultimately reduced ingestion of resistant E. coli (K C and the fraction of resistant E. coli in ingesta: ρ = −0·50, P < 0·001). The magnitude of the effect was not sizably enhanced if maximum E. coli numbers were simultaneously reduced in water in troughs or in feed in bunks (Fig. 6).
Plasmid-curing resistant enteric E. coli (without a reduction in their propensity to receive new AMR plasmids) was also highly efficient (Figs 6, 7 b). There was a very minor synergistic effect if the intervention was simultaneously applied to E. coli in the feed bunks (Fig. 6 a). The sensitizing significantly decreased faecal shedding of resistant E. coli (P C, varying from 0 to 0·2, and the number of resistant E. coli/ml of the steers' faecal deposits by the end of rearing: ρ = −0·78, P < 0·001); a consistently low fraction of resistant E. coli in ingesta with a P C intervention did not contain enough variability to estimate the degree of correlation with this outcome (data not shown). Plasmid-curing E. coli in the feed bunks by itself was associated with lower E. coli fractions in ingesta and the intestines; however, the degree of effect was modest compared with that when targeting enteric E. coli (Fig. 6). A similar effect was not observed for plasmid-curing E. coli in the water in troughs, because of the high degree of turnover of water due to consumption and re-fill.
An intervention lowering the rate of plasmid transfer in E. coli in the enteric habitat was also efficient (Fig. 7 c). Killing the plasmid-donor cells did not sizably enhance this effect (Fig. 6). Because of a relatively low number of resistant E. coli attempting to conjugate, the main impact of killing these cells was a reduction in plasmid transfer. The effects of lowering the transfer rate, whether by killing the donor cells or via another mechanism, by less than 40% were sensitive to variation in the other parameters of bacterial ecology and therefore uncertain. The effects were stable if the transfer rate was reduced further (Fig. 7 c).
Another target for an efficient intervention may be the rate of replacement of enteric E. coli with that ingested (given a lower fraction of resistant E. coli in ingesta). With a 10% daily replacement throughout rearing, the median final fraction of resistant enteric E. coli over 100 model simulations was 57·4%, with the base value used in this study of 24% daily replacement it was 10·4%, and with a 50% daily replacement it was 3·9% (Fig. 7 d). In our previous research [Reference Volkova, Lanzas, Lu and Grohn34], with the enteric plasmid transfer rates adopted from in vivo experiments [Reference Daniels32], the relatively low fractions of ceftiofur-resistant faecal E. coli in beef cattle reported by field studies could only be reproduced by allowing for regular partial replacement of enteric E. coli with that ingested (see also Fig. 7 d). Notably, then and now, we modelled enteric E. coli under ‘normal’ conditions, without disturbance by exogenous factors such as in-feed or parental antimicrobials. However, in the current model that accounted for ecology of resistance in E. coli in the pen's non-animate habitats, the final fraction of resistant enteric E. coli (median over 100 model simulations) was slightly higher, 2·7%, than that at steer placement, 2·0%, even if all enteric commensal E. coli were replaced daily (Fig. 7 d). These findings support an earlier hypothesis that controlling plasmid-mediated AMR in cattle faecal E. coli requires a more comprehensive understanding of the epidemiology of commensal E. coli, in particular its distribution and movement across hosts and habitats [Reference Daniels32].
Targeting interventions at reducing the replication rate of resistant E. coli (analogous to increasing the fitness cost to resistant E. coli) was not efficient. This may be because of a relatively slow growth of E. coli, a facultative anaerobe, in the enteric habitat, which appeared to be a crucial habitat for propagating plasmid-mediated AMR in commensal E. coli within the pen.
Lowering the total number of E. coli in the fresh water supplied to cattle (increasing intervention parameter K Wfr) was associated with a higher fraction of resistant enteric E. coli by the end of rearing (Fig. 6). Because the fractions of resistant E. coli within the pen steadily rose throughout rearing (Fig. 4) but the fraction of resistance in water supplied remained relatively low, E. coli from fresh water acted to ‘dilute’ the frequency of resistance in E. coli in cattle ingesta. On the other hand, further lowering the fraction of resistant E. coli in water or feed supply (within the ranges considered) did not significantly alter the final fraction of resistant enteric E. coli (υWfr and υFfr were not significant intervention targets).
It must be noted that given the biology of plasmid-mediated AMR (i.e. horizontal and vertical plasmid transfers) and expected variability in bacterial ecology in the field realm, one cannot state achieving which frequency of resistance in enteric E. coli would constitute a ‘success’. Hence, comparison of relative rather than absolute efficacy of interventions was the only feasible goal for this modelling study, and the model analysis was designed correspondingly (the non-parametric Spearman's correlation coefficient and the standardized regression coefficients). To better visualize the relative efficacies, we opted to present in Figure 7 box-and-whisker plots for all values of an intervention parameter until such value that the median fraction of resistant enteric E. coli at the end of rearing over 100 model simulations was equal to or below that at steer placement. In other words, the intervention mitigated the propagating impact of feedlot rearing on AMR frequency in enteric E. coli. The methods also ensured that the relative comparison of intervention effects did not depend on the actual frequency of resistance. For example, with qualitative interference from Figure 7, one would expect an intervention inducing plasmid-curing to outperform the one reducing plasmid transfer rate, if both achieved the same fractional change in the targeted parameter of bacterial ecology, irrespective of the starting AMR frequency in that E. coli population.
A change in the target parameters may be induced through different biological mechanisms. Table 2 provides examples of existing and potential biological intervention approaches that have been shown or are hypothesized to affect bacterial ecology in similar ways to those modelled. The feasibility of achieving a particular reduction in a target parameter (to compare with Fig. 7) by the existing approaches in the field realm is generally unknown.
In terms of potential intervention approaches that were not considered, a recent proof of concept study shows that, at least with some AMR mechanisms, the resistant bacteria can be rendered to become sensitive by genetic material delivered by constructed phages [Reference Edgar45]. Presumably, this could sensitize bacteria without plasmid loss, with the phages essentially acting as adjuvants for antimicrobials [Reference Lu and Collins27]. Such an intervention was not included because the related research is at too early a stage to support a mathematical formulation of the resulting plasmid ecology. Introducing new plasmid types for ‘incompatibility curing’ resistant bacteria from AMR plasmids has been researched in the past [Reference Trevors28]. However, given current knowledge on plasmid ecology, it would probably not be acceptable from a safety standpoint [Reference Edgar45], and therefore was not modelled.
Another intervention that was not considered was killing E. coli without altering the size of the niche available for their population growth (the latter was represented in the model by maximum E. coli numbers in the habitat). First, it is difficult to distinguish which of the two effects a given intervention produces. For example, water sanitization may be thought of as ‘killing’ E. coli; however, essentially, it controls the density of bacteria in this habitat. Second, altering the niche by introducing competitive microflora would be a more self-sustainable intervention compared to the continuously enforced kill.
Insights from this modelling study could help understand the field observations for some of the compounds tried for application in food animals to limit AMR spread in their enteric bacteria. For example, it is unlikely that the observed effects of in-feed bambermycins [Reference Dealy and Moeller19, Reference van den Bogaard20] correspond to a mere reduction in replication of plasmid-bearing Enterobacteriaceae. More likely, the in vivo action either reduces the plasmid transfer (perhaps via selective kill of plasmid-donor cells), or both does this and reduces the replication. Given that the effect of bambermycins on the transfer rate is plasmid-dependent, variability in the efficacy observed in vivo may be due to variable plasmid profiles of field E. coli.
Results of this modelling study also suggest that plasmid-mediated AMR in commensal E. coli can persist and propagate in feedlot operations even in the absence of use of therapeutic or growth-promoting antimicrobials. This is because the concentration of animals in the closed pen supports close circulation of E. coli between the enteric and non-animate habitats throughout the rearing period; this, coupled with high rates of AMR plasmid transfer in the intestines, in the current model led to a build-up of plasmid-mediated AMR in E. coli in all habitats. Presence of fitness cost for bearing AMR plasmids (even if high in magnitude, i.e. R C parameter) was insufficient to impede the propagation of resistance. Given the ‘natural’ presence of AMR plasmids in E. coli in the enteric and non-animate habitats, this means that discontinuing the use of antimicrobials in feedlot cattle alone may not be sufficient to prevent presence of resistant enteric E. coli in animal faeces (a vector of zoonotic transmission) at slaughter age. To prevent such a presence, the no-use policies may need to be coupled with either biological interventions into bacterial ecology producing the effects found significant in this study or disrupting E. coli circulation within the pens. However, the conclusions of this study are based on deterministic modelling, albeit with robust sensitivity and uncertainty analyses. Clarifying the likelihood of resistance extinction under the scenario of no-antimicrobial use with or without further interventions would require accounting for stochasticity in bacterial propagation and movement, and this will be the subject of future research.
ACKNOWLEDGEMENTS
We thank Julia Hertl of Cornell University for help with the statistical analysis. This work was funded by USDA NIFA grant no. 2010-51110-21083.
DECLARATION OF INTEREST
None.
