INTRODUCTION
Infection with the novel influenza A(H1N1v) virus emerged in Mexico in March 2009 rapidly spreading worldwide. The WHO reports that as of 17 October 2009 there have been over 414 000 laboratory-confirmed cases of pandemic influenza and almost 5000 deaths worldwide (http://www.who.int/csr/don/2009_10_23/en/index.html). However, to date, relatively little is known about the natural history of the infection with A(H1N1v) virus. Knowledge of its incubation period, the time from infection to onset of symptoms, is crucial to the understanding of the mechanism of transmission; to the recommendation of control measures such as contact tracing and quarantine; and to the formulation of transmission models aimed at predicting the healthcare burden [Reference Fraser1–Reference Reich5].
At the beginning of the current pandemic, the incubation period had been generically quoted to be either between 1 and 4 days (CDC, 5 May 2009) or between 1 and 7 days [6]. A rigorous systematic review of the incubation period of acute respiratory viral infections then led to the adoption of a median incubation time of 1·4 days for influenza A [Reference Lessler2] in some of the work on A(H1N1v) transmission modelling (e.g. [Reference Lipsitch8]). A few attempts were also made to estimate the incubation period of the pandemic H1N1 2009 strain directly, by using information on exposure and symptom onset times from outbreaks [Reference Kar-Purkayastha9–Reference Cao12]. These attempts reported incubation times of 24 h, a mean incubation time of 2 days and a median of around 3 and 2 days, respectively. These results are, however, mainly based on limited data with no attempt at explicitly modelling them. More considered is the work by Lessler et al. [Reference Lessler13], who estimated the distribution of the incubation time from a school outbreak. The sample size is, in this case, reasonably large (n=119), but the sample is mainly composed of young adults in the 14–19 years age range. Similarly, Tuite et al. [Reference Tuite14] formally address the problem, suggesting a mean incubation time of 4·3 days; much longer than previously estimated. A thorough characterization of the distribution of A(H1N1v) incubation period is, therefore, still warranted.
In the current study, information on time of exposure to the A(H1N1v) virus and on onset of symptoms from laboratory-confirmed cases collected from the Health Protection Agency (HPA) in England and Health Protection Scotland in the period May–July 2009 is used to more fully characterize the incubation period distribution.
METHODS
Data sources
From the HPA's national influenza database used to monitor cases during the containment phase of response (FluZone), we extracted all laboratory-confirmed novel A(H1N1v) cases in England with known date of onset of symptoms and which additionally had some degree of information available on the timing of exposure to the novel A(H1N1v) virus (either date of first or last exposure or ideally both these dates). The data obtained from FluZone were checked for completeness and consistency, and clarification on apparent anomalies were sought from the HPA units that had recorded the data. Data obtained from FluZone covered the period from 22 May 2009 up to 10 July 2009, after which FluZone was no longer used for monitoring the swine influenza pandemic. Furthermore, data on other confirmed cases with onset and exposure information available, but not in FluZone, were obtained from additional sources; specifically Regional HPA units in England and from Health Protection Scotland over the same time period. These other sources included data on investigated clusters linked with schools, a social gathering and a hospital. They provided an additional 63 confirmed swine influenza cases.
Statistical analyses
Exact times (in days) to symptom onset from infection by the novel influenza A(H1N1v) virus were only known for confirmed cases who had point (i.e. single day) exposure contact with known index cases and those whose first known exposure date coincided with their date of onset (i.e. those with an exact exposure date). For the remaining cases (who were the majority) less precise data were available on the incubation time, which could only be assessed to fall within an interval (interval-censored incubation times) or to be longer (right-censored incubation times) or shorter (left-censored incubation times) than a specific length of time. We employed parametric survival analysis to analyse and characterize the data on incubation times. Models based on assuming log-normal, Weibull and gamma distributions for the incubation times were fitted and, from their estimated distributional parameters, means, medians and standard deviations for the incubation times were calculated for symptomatic swine influenza cases. A non-parametric maximum-likelihood estimator (NPMLE) of the incubation distribution was also constructed using the R package MLEcens [Reference Maathuis15] assuming that the boundaries of the interval-censored incubation times are opened on the left and closed on the right. All analyses were performed using the R statistical package [16].
Cases for which apparent inconsistencies in the data could not be resolved were excluded from analyses. Analyses were performed on various subsets of the collated data, beginning with the subset of cases for which exact incubation times could be obtained through knowledge of the exact exposure dates. This was then followed by the addition to this initial subset of those cases with both distinct first and last dates of exposure available. For these the exposure was only known to have occurred within an interval, thus producing interval-censored incubation times. Those with only a first date of exposure available (left-censored incubation times) were then added to the enlarged subset; and finally those with only a last exposure date known (right-censored incubation times) were included to constitute the full use of all available data (see Table 1). In addition, analyses based on FluZone and non-FluZone data were performed; as were age-stratified analyses in which age was dichotomized into two groups (<15 years and ⩾15 years). Note that for the cases characterized through knowledge of the exact exposure dates we treated incubation times of ⩾1 day as being ‘exact’ in the survival analysis, while for those with incubation times <1 day due to the exposure date coinciding with the onset date, we treated these incubation times as being left-censored (<1 day) in the survival analysis.
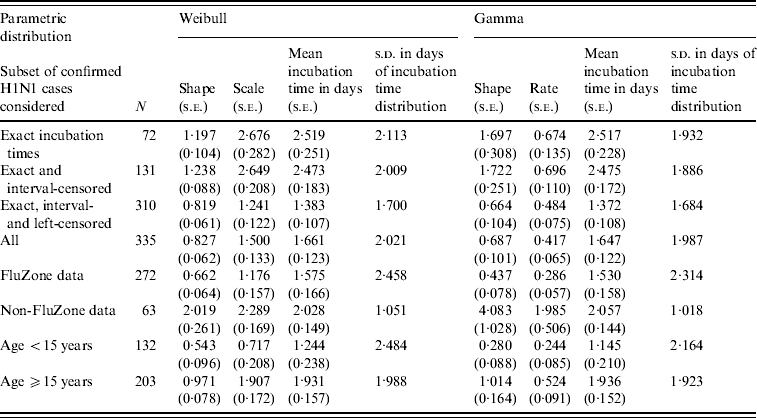
Table 1. Results from parametric time-to-event analyses of various subsets of the swine influenza dataset considered
RESULTS
Table 2 provides the background characteristics of the FluZone database, including the 323 individuals with exposure information, and for the data (n=63) from the additional sources mentioned above. The dataset collated for analysis comprised 386 individuals who were confirmed as being infected with A(H1N1v) virus and had a recorded date of onset of symptoms with additional information on probable first and/or last exposure dates. About half were male. Fifty-one of these 386 individuals had dates which were queried but remained unresolved and were therefore removed from the dataset. This left data on 335 individuals for analysis, of which 132 (39·4%) were aged <15 years. Of these 335 individuals, 72 were cases in which the exact incubation time could be ascertained, 59 had interval-censored incubation times, and 179 and 25 had left-censored and right-censored incubation times, respectively. The age distribution differed across the different types of incubation information (P<0·001), with the lowest percentage of under-15s (20·8%) found in the exact incubation time group. About half of the interval-censored group (49·7%) were aged <15 years, while 35·6% and 28% of the left-censored and right-censored groups were aged <15 years, respectively.
Table 2. Background characteristics of patients in the FluZone database and additional data sources
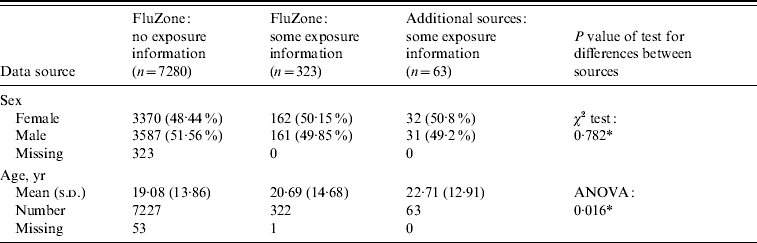
* Ignoring missing data when performing the tests for difference.
Table 1 shows the results obtained for the parametric Weibull and gamma analyses performed on the various subsets of the data. The results for log-normal are not presented as this model produced a much poorer fit to the data. There was a significant difference in the proportion of onset times ⩽1 day for the exact, interval-censored and left-censored groups (P<0·001). The left-censored group had a far greater proportion than both the exact and interval-censored groups and this difference was reflected in the estimates of the mean incubation times reported in Table 1 between the second and third subsets of confirmed cases. For the entire dataset of 335 confirmed cases, the parametric Weibull and gamma models estimated the mean incubation time to onset of symptoms to be 1·661 days (95% CI 1·420–1·902) and 1·647 days (95% CI 1·408–1·886), respectively. The estimated mean incubation times across the various subsets considered ranged from about 1·4 days to 2·5 days. The mean incubation time estimated from NPMLE was between 2·043 days and 2·137 days. The estimated median incubation times to onset of symptoms (i.e. the times by which 50% of the confirmed cases are expected to show symptoms) for the entire dataset under the Weibull and gamma models were 0·963 (95% CI 0·765–1·174) and 0·948 (95% CI 0·717–1·158) days, respectively. The corresponding 95th percentiles were 5·653 (95% CI 4·759–6·832) and 5·646 (95% CI 4·889–7·003) days, respectively.
Analysis performed using only non-FluZone data gave a mean incubation time of around 2 days (s.d.=1 day). Results from the age-stratified analyses are also shown in Table 1. From these results it appears that there is a difference between the mean incubation times for individuals aged <15 years and those aged ⩾15 years, irrespective of the model used. Mean differences from the Weibull and the gamma models were 0·688 (95% CI 0·129–1·246) and 0·792 (95% CI 0·284–1·300) days, respectively. These differences are significant at the 0·02 level. Additionally, the estimated median incubation times from these two models were 0·365 (95% CI 0·124–0·659) and 0·248 (95% CI 0·012–0·521) for those aged <15 years; and 1·308 (95% CI 1·041–1·569) and 1·350 (95% CI 1·032–1·603) for those aged ⩾15 years.
Figure 1 plots the non-parametric and parametric cumulative distribution functions obtained from analysing the full dataset of 335 confirmed cases, showing the cumulative proportion of cases developing symptoms by each day. These estimates are similar and suggest that the parametric Weibull and gamma models fit the data reasonably well. Figure 2 shows the bar plots of the probabilities of symptom onset each day after infection, up to day 10, derived from the parametric Weibull and gamma incubation models. Here it is difficult to differentiate between the models which is reflected in their similar estimates of the mean incubation time and standard deviation (Table 1). However, on fitting a three-parameter generalized gamma model [Reference Farewell and Prentice17] for which both the Weibull and gamma (as is the log-normal) models are special cases, there is an indication that the Weibull is marginally more appropriate, in terms of having similar parameter estimates to the generalized gamma model and a slightly larger log-likelihood than the gamma model.
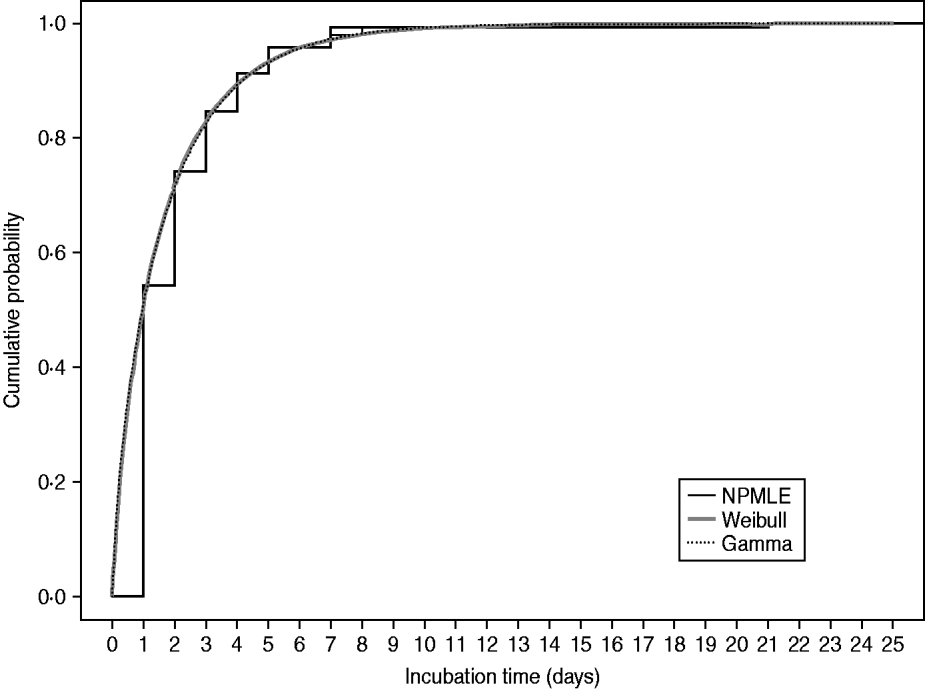
Fig. 1. Estimated cumulative distribution functions for the incubation times of the 335 confirmed symptomatic cases considered. NPMLE, Non-parametric maximum-likelihood estimator.

Fig. 2. Estimated probability of symptom onset each day after infection, up to day 10, for the 335 confirmed symptomatic cases considered.
DISCUSSION
There is still substantial amount of uncertainty regarding the incubation period for the 2009 pandemic A(H1N1v) virus. Earlier attempts to estimate the incubation period were primarily based on limited data or on peculiar samples. In this work, we have characterized the incubation distribution using data from 335 laboratory-confirmed cases, both adults and children, derived from HPA's FluZone database for England and from additional sources, including Health Protection Scotland. The size and composition of this sample and the fact that all individuals included were confirmed as having had A(H1N1v) virus allowed us the unique opportunity to more fully characterize the incubation distribution of the population of symptomatic individuals in the UK, and provide a more precise estimate of the mean incubation time. Moreover, the timing of the sample collection, early in the epidemic, might have improved the likelihood of accurate exposure reporting as the population was mostly naive and cases more directly related to travel-acquired infections.
We obtained a mean incubation time for symptomatic individuals of 1·6–1·7 days (s.d.=2 days). The median incubation time was found to be between 0·9 and 1 day. Our estimated mean and median incubation times are somewhat comparable to the median incubation time of 1·4 days obtained for influenza A [Reference Lessler2], and our results for individuals aged ⩾15 years agree with those obtained using data from a New York City school outbreak on mainly young adults aged 14–19 years [Reference Lessler13]. Additionally, our estimates are consistent with the earlier mentioned times of 24 h and 2 days for the UK pandemic, although lower than the suggested median of around 3 days reported for the pandemic in Spain [11]. On the other hand, they seem at odds with the mean incubation time of 4·3 days reported by Tuite et al. [Reference Tuite14] using a log-normal distribution but without directly accounting for the interval-censored nature of the data.
Our study may suffer from selection bias as those positive cases who were not laboratory-confirmed may be different from those positive cases whose swabs were sent for laboratory confirmation; e.g. in the severity of their illness, with those laboratory-confirmed having a more severe illness. However, there was, in general, good ascertainment and laboratory testing of suspected cases up to the 10 July 2009, after which the FluZone database was no longer used for monitoring the swine influenza pandemic. As most of our cases were from the period before 10 July 2009, we are reasonably satisfied that there were few positive cases that developed symptoms and were not tested. Another possible source of selection bias in our study was the use of laboratory-confirmed cases that provided exposure information only. This group of cases may systematically differ from those laboratory-confirmed cases that had no recorded exposure details in ways that may be associated with time to symptoms from infection. However, it is unclear how these cases without exposure information and without detailed contact information could have been used here. Moreover, no obvious difference in sex distribution was seen (Table 2) and only a very marginal statistical difference (P=0·04) of 1·6 years was noted between the mean ages.
In this study we have assumed that the date of onset of symptoms was known exactly, while the exact date of infection with A(H1N1v) virus was only known for a minority of cases. This uncertainty in infection date for the majority of cases hampers analyses, and statistical methods (such as parametric distributional models) that handle interval-censored data are required to characterize the incubation distribution. Other approaches for estimating the incubation period distribution that do not rely on the time of infection, e.g. from serial interval data [Reference Kuk and Ma18], were considered but found unfeasible. Additionally, it is quite plausible that cases may have inaccurately reported the exact date when their symptoms first arose, although it is unclear in what direction this misreporting would be. If, in addition to uncertainty in the exact infection date, the onset of symptoms date was known to fall within an interval, then methods for handling such doubly interval-censored data would be required [Reference Reich5].
Our study, with all the provisos expressed above, provides a fuller characterization of the incubation distribution for a generic group of symptomatic cases infected with the novel A(H1N1v) virus. Not only have our analyses provided an estimate of the mean (or median) incubation time, which appears to be reasonable, but they have provided us with a well fitting characterization of the entire incubation distribution, based either on the Weibull or gamma parametric models, which also appropriately accounts for interval-censoring. A parametric representation of the incubation distribution will allow us to examine different aspects of the distribution (e.g. the 95th percentile) that are important for deciding containment strategies, identifying the source of infection and for the formulation of transmission models aimed at predicting the healthcare burden, as advocated, for instance, by Lessler et al. [Reference Lessler2]. Furthermore, from our analyses we have found evidence for a difference in the mean incubation times for the <15 years and ⩾15 years age groups, with a longer mean incubation time in the older age group. This finding, which has not been shown previously for influenza, may have implications on how these two age groups are treated in terms of the prioritizing of resources.
In conclusion, our characterization of the incubation time for the novel A(H1N1v) virus will hopefully contribute to a better understanding of the spread of this pandemic and aid in its control and management.
ACKNOWLEDGEMENTS
The authors thank the epidemiologists from the various Health Protection Agency units in England for their assistance in answering queries relating to the data. Brian Tom was financially supported by the UK Medical Research Council (MRC grant U.1052.00.009). Daniela De Angelis was funded by the UK Health Protection Agency and the UK Medical Research Council (MRC grant U.1052.00.007).
DECLARATION OF INTEREST
None.






