INTRODUCTION
Humans infected with E. coli O157 may show a range of clinical outcomes including asymptomatic shedding, gastroenteritis, haemorrhagic colitis, and/or haemolytic uraemic syndrome [Reference Ochoa and Cleary1]. Infection with E. coli O157 has been associated with exposure to contaminated food [Reference MacDonald2, Reference Hilborn3], contaminated drinking and recreational water [Reference Hrudey4, Reference Bruce5], shedding humans and animals [Reference Galanis6, Reference Pritchard7], and contaminated environments [Reference Howie8]. The young and elderly are often considered to be at the greatest risk of infection and/or complications following infection with E. coli O157 [Reference Ochoa and Cleary1, Reference Havelaar9–Reference Dundas11]. Due to the potential severity of clinical symptoms, the level of underreporting of clinical cases is lower than disease associated with many other enteric pathogens [Reference Mead12, Reference Michel13]. Current knowledge concerning risk factors associated with E. coli O157 comes generally from the analysis of databases on outbreaks and sporadic cases kept by public health agencies [Reference Rangel14–Reference Locking16].
In a previous study in Alberta, Canada, we found variation in the spatial distribution of reported outbreak and sporadic cases [Reference Pearl17]. We also demonstrated that the location of areas with significantly higher rates of E. coli O157, after correcting for demographic factors, was impacted by the choice to use only sporadic cases or both sporadic and outbreak cases in our statistical analyses. Subsequently, we questioned whether the mode and site of transmission and the characteristics of individuals that became infected with E. coli O157 were different depending on whether they were identified as a sporadic or outbreak case (i.e. two or more cases related to a common exposure). Understanding these differences may have important implications for which groups and activities should be targeted for disease prevention programmes or increased surveillance. Studies on secondary transmission of E. coli O157 and a number of outbreaks dominated by children suggest young children may be at increased risk of being involved in outbreaks [Reference Galanis6, Reference Parry and Salmon18].
Comparing outbreak and sporadic cases may pose some analytical challenges. Cases associated with a particular outbreak are not independent. Ignoring this lack of independence can result in an underestimation of variability and increase the probability of making a type I error (i.e. falsely rejecting the null hypothesis) [Reference Schukken19–Reference Dohoo, Martin and Stryhn21]. It can also result in incorrect estimates of measures of association. A variety of techniques including robust variance estimates, general estimating equations (GEE), and random effects models have been created to deal with clustered data [Reference Schukken19–Reference Dohoo, Martin and Stryhn21]. However, in our study, only cases associated with outbreaks had a true hierarchical structure. Consequently, methods, such as GEE or random effects models, that correct both measures of association and measures of variance by accounting for the correlation among cases, may fail to converge or provide unreliable estimates if faced with few replications at a hierarchical level. Other possible techniques for controlling for clustering may include the random selection of one case from each outbreak to remove the clustering effect by design rather than through a statistical technique. Analytical weights could also be used to down-weight the impact of multiple cases from a single outbreak; similar approaches have been developed for dealing with complex survey designs where the probability of being sampled may vary among cases [Reference Dohoo, Martin and Stryhn21].
Using a database of reported cases of E. coli O157 from Alberta, Canada in 2000–2002, we determined whether there were significant differences between sporadic and outbreak cases in terms of age, sex, the mode of transmission (e.g. food), and the site of transmission (e.g. home). We also determined whether the following temporal, spatial, and administrative factors were significant predictors of whether a case was more likely to be part of an outbreak: a region in the province where there was a higher proportion of outbreak cases than sporadic cases (outbreak cluster) [Reference Pearl17]; a yearly period from May to October when reported cases cluster [Reference Pearl17]; year of study; and whether a case had been hospitalized. We also tested the significance of interactions between age, sex, and mode and site of transmission. We created multivariable logistic models using a variety of methods to correct for clustering for comparative purposes.
METHODS
Data
We obtained a list of all reported cases of E. coli O157 infection in Alberta during the 2000–2002 period. The data were obtained from Notifiable Disease Reports (NDR) stored electronically in the Communicable Disease Reporting System (CDRS) maintained by the Disease Control and Prevention Branch of Alberta Health and Wellness using methods designed to preserve patient anonymity. The protocol for this research was approved by the University of Guelph Research Ethics Board.
In total 875 cases were recorded during this period, but six cases were excluded from subsequent analyses because of insufficient demographic and/or spatial data [Reference Pearl17]. From the NDR we obtained/calculated the following information for each case: a unique identifier (NDR number), age at onset of clinical symptoms, year case occurred, sex, mode of transmission, site of transmission, case hospitalization (yes/no), a unique identifier used for community outbreaks (Exposure Indicator Number), cases identified through an epidemiological link that did not require definitive laboratory results (EPI-linked), the NDR numbers that connected EPI-linked cases, and a unique identifier created to identify cases sharing a common address. Mode of transmission included the following categories: food and water, animal contact, person-to-person, other, and unknown. Site of transmission included the following categories: home, food services establishment, high-contact housing (nursing home, daycare, campsite), travel, other, unknown. The categories for mode and site of transmission were slightly modified from the categories used in the NDR to avoid small cell sizes in subsequent statistical analyses. The ‘other’ category in the mode and site of transmission variables were known/suspected by the public health worker, but did not fall into the remaining categories. In the electronic database, only ‘other’ was recorded, but we added three observations, believed to be attributed to the pathogen being aerosolized, to the ‘other’ category for mode of transmission, and 20 cases believed to have occurred at the workplace to the ‘other’ category in site of transmission. Cases were classified as outbreak cases if they shared a common Exposure Indicator Number, were Epi-linked, and/or shared a common address. Based on the above definition, cases associated with an outbreak were given a unique outbreak number. In total, there were 69 outbreaks involving 185 cases. The largest outbreak recorded in the database included 10 cases. However, 53% of all outbreak cases were in outbreaks involving two individuals.
Two variables in this study were based on the results of previous analyses of these data using SaTScan version 3.1.2 [Reference Kulldorff22]. We created variables to identify a region in the province with an increased proportion of outbreak cases relative to sporadic cases based on a Bernoulli model (outbreak cluster), and a period of time variable when the rate of cases was increased based on a Poisson model (seasonal cluster) [Reference Pearl17, Reference Kulldorff22]. Cases that were classified as being part of the outbreak cluster were located in a region with an approximate latitude and longitude of 50° N and 112° W, and a radius of 78 km. Cases that were classified as being part of a seasonal cluster fell between 1 May and 31 October in 2000–2002.
Statistical analyses
All of the multivariable statistical models created for this study involved a dichotomous outcome (i.e. outbreak/sporadic). The assumed distribution of the response variable was binary, and a logit link was used between the response variable and its linear predictor. All tests performed were two-tailed tests with a statistical significance level of 5%. In addition to descriptive statistics, univariable statistics were also performed for each variable with a t test, adjusted for unequal variances, being performed for age and χ2 tests being performed for categorical variables.
Prior to beginning the model-building procedure, we determined whether there was a strong correlation among any of the predictor variables. If the correlation between two variables was ⩾0·8, based on a Pearson's or Spearman's rank correlation coefficient, only one of the variables would be used in subsequent analyses. In addition, we tested the assumption of linearity for age using three techniques: including a square term in the model; categorizing the continuous predictor to determine if the coefficients increased in a relatively uniform fashion; and plotting the log odds of the outcome against the mean of 10 categories of age divided into 10 percentiles. If any of these methods revealed that the assumption of linearity was violated, the appropriate transformation was performed or if significant, a square term was added to the model.
The initial model-building procedure began with an ordinary logistic regression model (i.e. a logistic regression model that did not account for clustering in the data). Interaction terms and square terms were added individually to the full model (i.e. a model with all the main effects) and were removed if they were not statistically significant. Main effects were removed one at a time and kept in the final model if they were statistically significant based on a likelihood ratio test or acted as a confounding variable. A confounding variable was defined as a variable that caused at least a 20% change to the coefficient of a statistically significant variable on a log odds scale when it was removed from the model. All main effects that had been removed were re-introduced to the final model one at a time to re-assess their significance and potential confounding effect. When re-introducing interaction effects to a tentative final model, all necessary base terms were also included. The Hosmer–Lemeshow goodness-of-fit test was performed to determine that the binary model was appropriate for the data. A likelihood ratio test was used to assess the significance of removed variables where the estimates were calculated using maximum-likelihood procedures. Where a quasi-likelihood method was used, significance was assessed using Wald tests.
While our initial modelling procedures involved an ordinary logistic regression model, we looked at a number of procedures to correct for the impact of clustering [Reference Schukken19, Reference Dohoo, Martin and Stryhn21]. We employed the following two techniques that adjusted the variance estimates but not the coefficient estimates themselves: robust variance estimates based on Huber–White/sandwich variance estimates that are less sensitive to the assumption of independence; and robust variance estimates with a ‘cluster’ option that specifies that observations are independent across groups (i.e. cluster) but not necessarily within groups [Reference Dohoo, Martin and Stryhn21]. The following models adjusted both the coefficient estimates and the variances: a weighted logistic regression model where a weight was applied to each observation that was the inverse of the number of cases within an outbreak or one if the case was sporadic; GEE with an exchangeable correlation structure; and random intercept models using various algorithms [Reference Dohoo, Martin and Stryhn21]. Random intercept models were performed/attempted using: various combinations of predictive quasi-likelihood (PQL) or marginal quasi-likelihood (MQL), and first- or second-order derivatives of the Taylor series expansion for linearization prior to the use of re-weighted iterative generalized least squares (RIGLS); the Monte Carlo Markov Chain (MCMC) method; and generalized linear latent and mixed models (GLLAMM) [Reference Goldstein20, Reference Skrondal and Rabe-Hesketh23]. In addition, we controlled for clustering prior to building a logistic model by randomly selecting one case from each outbreak. This procedure was performed five times to determine whether the coefficients calculated for each variable were relatively stable among iterations.
Residual analyses were performed for the ordinary logistic regression model and the random effects model produced using RIGLS, PQL, and first-order derivatives of the Taylor series expansion. Residuals were inspected for extreme standardized residuals, high leverage, and high influence. All statistical analyses were performed using Intercooled Stata 8.0 for Windows (Stata Corp., College Station, TX, USA) except for the random effects models involving quasi-likelihood or MCMC methods which were performed using MLwiN 2.02 (Institute of Education, London, UK). The weights for the weighted logistic regression were applied using an ‘iweight’ option. The weights were applied to the likelihood function in a manner similar to those used to adjust for different probabilities of being sampled [24].
RESULTS
Based on univariable statistics the following variables had a statistically significant association with the dependent variable (i.e. outbreak/sporadic): age, outbreak cluster, case year, mode and site of transmission (Table 1). The correlations among all the independent variables used in our study never exceeded 0·8. Age was log transformed (natural log) since it did not have a linear relationship with the outcome based on a log odds plot.
Table 1. Univariable statistics comparing reported outbreak and sporadic cases from Alberta, Canada in 2000–2002

For categorical variables, the number of cases and their relative proportions (in parentheses) are indicated. In the case of continuous variables (i.e. age), the mean and standard deviation (in parentheses) are indicated. t tests and χ2 statistics were used for continuous and categorical variables, respectively.
Within the ordinary logistic regression model the following variables were not statistically significant based on a likelihood ratio test (χ2=11·81, d.f.=11, P=0·38) and were removed from the full model: sex, hospitalization, case year, temporal cluster, and site of transmission. These terms did not have a confounding effect on the remaining significant variables. A square term for the log of age in years (χ2=3·13, d.f.=1, P=0·077), and interaction terms among age and sex (χ2=0·02; d.f.=1; P=0·90), age and mode of transmission (χ2=3·54, d.f.=4, P=0·47), sex and mode of transmission (χ2=3·23, d.f.=4, P=0·52), age and site of transmission (χ2=4·13, d.f.=5, P=0·53), and sex and site of transmission (χ2=6·47, d.f.=5, P=0·26) were also statistically non-significant when added to the full ordinary logistic regression model. The model-building process for the various logistic models designed to control for clustering resulted in models with the same fixed effects.
The final main effects models included the following variables: log of age in years, outbreak cluster, and mode of transmission (Table 2). The Hosmer–Lemeshow goodness-of-fit test for the ordinary logistic regression model was non-significant (Hosmer–Lemeshow χ2=5·20, d.f.=10, P=0·74) indicating that the binary model was appropriate. The direction of odds ratios for all the variables was the same among all the models (Table 2). The confidence intervals were generally larger for all models using methods designed to account for clustering (Table 2). However, applying the robust option to relax the assumption of independence among observations often resulted in narrower confidence intervals (Table 2) than those produced by our ordinary logistic regression model. Among methods designed to adjust the odds ratios and variance estimates, the random effects model employing PQL and the weighted regression model had almost identical odds ratios and 95% confidence intervals (Table 2). The odds ratios estimated using MQL were closer to the null among the statistically significant coefficients. The direction of odds ratios for significant variables was similar among the five models (Random 1–5) where a single case was randomly selected from each outbreak, although there was some variation in the point estimates and confidence intervals (Table 2). The model using GEE with an exchangeable correlation structure failed to converge. Estimates obtained using GLLAMM and MCMC methods when converted to an odds scale were several orders of magnitude greater or smaller, depending on the direction of the association, from those obtained using the other methods.
Table 2. The odds ratios and 95% confidence intervals (in parentheses) for all variables in our final multivariable models, using various methods to deal with clustering, comparing reported outbreak and sporadic cases from Alberta, Canada in 2000–2002
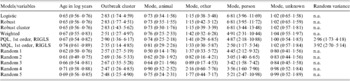
n.a., Not applicable; Logistic, an ordinary logistic regression; Robust, robust variance estimates; Robust cluster, robust variance estimates accounting for the hierarchical structure; Weighted, weighted regression; PQL, predictive quasi-likelihood; RIGLS, re-weighted iterative generalized least squares; MQL, marginal quasi-likelihood; 1st order, first order derivative of the Taylor series expansion; Random (1–5), five iterations of a logistic regression where one case is randomly selected from each outbreak; Random variance, variance component of the random intercept.
Increasing age appeared to have a statistically significant sparing effect, while cases found within the Bernoulli cluster were at increased risk of being outbreak cases (Table 2). Using food and water as the referent category, individuals believed to have obtained their infection from another person were at increased risk of being in an outbreak (Table 2). We also found significant differences in animal (χ2=27·10, d.f.=1, P<0·001), other (χ2=9·24, d.f.=1, P=0·002), and unknown (χ2=43·23, d.f.=1, P<0·001) modes of transmission relative to person-to-person spread based on Wald tests applied to the ordinary logistic regression model. However, there was no significant difference between person-to-person transmission and the ‘other’ category for transmission when the following models/methods were employed to adjust for clustering: weighted regression (χ2=2·53, d.f.=1, P=0·11); random effects model with PQL (χ2=2·22, d.f.=1, P=0·14); random effects model with MQL (χ2=0·68, d.f.=1, P=0·41); randomly selecting a case from each outbreak (χ2=0·52–2·46, d.f.=1, P=0·12–0·47). There was no statistically significant relationship among the other modes of transmission. The residual analyses based on the ordinary and random effects logistic regression models did not identify any observations that were highly unusual or that had a large impact on the model when removed.
DISCUSSION
Age, mode of transmission, and a variable marking the spatial location of a cluster of outbreak cases (i.e. outbreak cluster) were the only significant variables in our final models. The proportion of female and summer cases appeared to be higher than male and non-summer cases respectively during the 2000–2002 period (Table 1), but there appears to be no strong association between these variables and whether a case is sporadic or part of an outbreak. This suggests that the mechanisms behind determining whether a case is independent or part of an outbreak are not simply a reflection of risk factors associated with disease.
On a log scale, increasing age appeared to have a sparing effect on the risk of a case being linked to another case in the CDRS. This could be explained by the increased tendency of young children to sample their environment orally and practice poorer personal hygiene. There are many examples of outbreaks of E. coli O157 among young children associated with secondary transmission among children or exposure to shedding animals in farms or petting zoos [Reference Galanis6, Reference Pritchard7, Reference Crump25]. A potential alternative hypothesis could be that the severity of disease in young children increases the effort or ability of health workers to make epidemiological links among cases [Reference Rowe26]. However, cases that were hospitalized were not more likely to be linked to an outbreak, and there was no evidence to suggest that the risk of being linked to an outbreak increased again with advanced age when the impact of infection with E. coli O157 can be more severe [Reference Strausbaugh, Sukumar and Joseph27].
Within the mode of transmission, only person-to-person transmission was significantly different from other categories. Depending on the model, a case was almost five times more likely to be within an identified outbreak if the public health worker believed that the mode of transmission was person-to-person compared to cases where the mode of transmission was related to food or water. Based on our definition of an outbreak (i.e. two or more cases linked epidemiologically), this finding was not surprising. In fact, it may be more important to note that nearly a third of cases where the mode of transmission was believed to be person-to-person remained unlinked to another case in the CDRS (Table 1). This may suggest that many outbreaks or cases associated with an outbreak remain unlinked or undetected. However, it is important to recognize that the sensitivity and specificity of questions concerning the mode and site of transmission of disease are likely to be different between truly sporadic and outbreak cases (i.e. differential misclassification bias). By virtue of being independent, the investigation of sporadic cases cannot be supported with statistical measures used to investigate outbreaks [Reference MacDonald2, Reference Galanis6, Reference Duffell28]. As a result, we may be less certain about these classifications for sporadic cases.
Clustering or the lack of independence among observations is an important issue for obtaining appropriate measures of association and variance. In our study, clustering was an issue in terms of space and the grouping of cases into outbreaks. The inclusion of a variable to control for cases located within a spatial cluster of outbreak cases, identified in an earlier study [Reference Pearl17], removed the possibility that our results were simply being driven by the clustering of 27% of our outbreak cases into a relatively small geographical area. A variety of more complex techniques are available to adjust for spatial autocorrelation [Reference Fotheringham, Brunsdon and Charlton29], but we were able to create a simpler model using a fixed effect that was well delineated from our previous study [Reference Pearl17]. On the other hand, modelling our outbreaks as fixed effects would have resulted in the introduction of a large number of variables into our model and the parameter estimates would have become unstable with relatively few observations per group [Reference Dohoo, Martin and Stryhn21]. In addition, we were faced with the unusual circumstance where sporadic cases, unlike outbreak cases, did not have a true hierarchical structure. Consequently, we wanted to compare a number of options for handling clustered data.
To create the most extreme scenarios, we created an ordinary logistic regression model that did not control for clustering, and five models where each time we only selected one case per outbreak (Table 2). Both types of models gave us reasonable expectations concerning the direction and relative size of the measures of association. Consequently, we were able to reject models generated by MCMC methods and GLLAMM that had strikingly different measures of association. However, these two models had measures of association that were effectively reaching positive and negative infinity and would not have been accepted as biologically plausible. In addition, the GEE model and the random effects model using the second-order derivative of the Taylor series expansion failed to converge. The poor performance of some of the models was expected by virtue of the structure of the data. Random effects and GEE models are often used to adjust for a correlation structure among grouped observations. Typically, all the data have a hierarchical structure although the number of observations within a higher level of the hierarchy may vary. However, more than half of our data (i.e. sporadic cases) had no true hierarchical structure, although they were each assigned a grouping variable to perform these procedures. In addition, the correlation structure among observations within an outbreak was defined by our dependent variable (i.e. all cases in an outbreak are classified as outbreak cases).
Among the models that produced reasonable estimates, the confidence intervals associated with the model using robust variance estimates tended to be equal to or somewhat smaller than those produced by an ordinary logistic model that ignored clustering. Once the clustering effect was accounted for in the variance estimates, the more conservative confidence intervals, that were expected, were achieved (Table 2). The random effects models based on pseudo-likelihood methods worked reasonably well, although, as expected, the model using MQL for linearization tended to have odds ratios closer to the null [Reference Rasbash30]. Surprisingly, the random effects model using PQL and the weighted logistic regression had unusually similar estimates for the odds ratios and confidence intervals of the significant variables in the final model (Table 2). These values also fell within the ranges predicted using a technique that only included one case per outbreak. Our attempt to weight cases by the inverse of the number of cases associated with an outbreak appears to be a valid approach based on these results. Unlike random effects models, this technique does not provide variance estimates for the different levels in the hierarchy of the data, however, understanding this structure does not have biological meaning in the context of this study.
The results of our study have both epidemiological and methodological implications. The increased risk for young children to be in outbreaks suggests that more attention needs to be paid to issues that place children at greater risk of exposure to point sources of infection that cause outbreaks. Unfortunately, our inability to find interaction effects between age and mode or site of transmission does not provide a specific activity or area to target. Even with 3 years of data, it is obvious that our power to detect interaction effects may be limited when comparing age to a variable with a large number of categories. In terms of methodology, we have found that using weights to account for the size of an outbreak is a useful and robust approach for dealing with clustering when comparing outbreak (i.e. clustered) to sporadic (i.e. independent) cases.
ACKNOWLEDGEMENTS
We thank Ian Dohoo and Henrik Stryhn for providing a number of useful suggestions for analysing our data. D.L.P. has been supported by fellowships and awards from the Canadian Institutes of Health Research and the Ontario Veterinary College. We also acknowledge the support of the Wellcome Trust through the International Partnership Research Award in Veterinary Epidemiology.
DECLARATION OF INTEREST
None.




