INTRODUCTION
The influenza virus causes widespread morbidity and mortality in various populations: an average of 250 000–500 000 deaths occur every year worldwide [1]. In subtropical regions like Taiwan, this impact is felt predominantly during the winter months, and the epidemics recur with a highly predictable seasonal pattern. Seasonal variation in disease transmission thus plays an important role in the transmission dynamics of influenza. Since schools are centres for the spread of influenza, the probability of disease transmission is considerably higher due to increased mixing level of people during school terms compared to school holidays [Reference Ridenhour2].
Our previous studies [Reference Liao, Chang and Liang3–Reference Chen and Liao5] have focused on both the theoretical and empirical aspects of the transmission dynamics of indoor respiratory infections. These were aimed at both understanding observed epidemiological patterns and predicting the consequences of introduced public health interventions along with effective engineering control measures to contain infectious diseases.
A Wells–Riley mathematical model was employed for modelling indoor respiratory infection [Reference Liao, Chang and Liang3–Reference Chen and Liao5] to estimate the exposure concentrations (q) in indoor environments and to estimate the basic reproduction number (R 0) in a shared indoor airspace. Riley et al. [Reference Riley, Murphy and Riley6] developed a Wells–Riley mathematical equation to estimate the probability of airborne transmission of an infectious agent indoors. The key parameter is the quantum generation rate (q) of infectious quanta by an infected person. The q value was defined by Wells [Reference Wells7] who conducted a series of experiments to estimate the response and reaction to inhaled infectious droplets, indicating that a quantum (or infectious dose) can infect 63·2% of susceptibles tested. Hence, exposure to one quantum of infection gives an average probability of 63% of becoming infected [Reference Wells7]. The R 0 value is the key epidemiological determinant that characterizes the transmission potential of a disease, which is defined as the average number of successful secondary infection cases generated by a typical primary infected case in an entirely susceptible population [Reference Anderson and May8]. R 0 essentially determines the rate of spread of an epidemic and how intensive a policy will need to be to control the epidemic. R 0>1 implies that the epidemic is spreading within a population and that incidence is increasing, whereas R 0<1 means that the disease is dying out. An average R 0 = 1 means the disease is in endemic equilibrium within the population.
We also adopted the competing-risks model [Reference Brookmeyer, Johnson and Bollinger9–Reference Brookmeyer, Johnson and Barry11] to understand the dynamics of the interplay in different enhanced engineering control measure strategies. The competing-risks model is a probabilistic model by which the dynamics of interplay in different enhanced engineering control-measure strategies can be described. The basic assumption of the probabilistic calculations on the competing-risks model was based on an underlying Poisson model, i.e. different control efficacies act independently of each other. The selected optimal control measures include environmental controls by ventilation and air filtration, as well as respiratory protection. The inclusion of competing risks in the model recognized the fact that an individual might gain substantial benefits in risk reduction of airborne infection from many different control measures including technological controls at the source (by surgical masking and treatment booths), environmental controls (by ventilation, air filtration and ultraviolet germicidal irradiation), and receptor controls (by respiratory protection via respirators) [Reference Nardell12–Reference Rudnick and Milton14].
We linked the competing-risks model and Wells–Riley mathematical equation in order to estimate the reduction of the potential infectious force of R 0. Finally, a susceptible-exposed-infected-recovery (SEIR) model was used for quantitatively explaining the dynamics of an epidemic. However, in our study, we ignored the control measure effectiveness variation and unit cost estimations.
The cost benefits of influenza vaccination were assessed for many countries; the methods of assessment and unit cost of control measures were different in each country [Reference Baguelin15, Reference Velasco16]. Published studies provide the cost analysis methods and consider the direct (hospitalization or vaccination) and indirect costs (parent work loss) of disease burden for comparison with different scenarios, such as the vaccinated coverage rate [Reference Acedo17] and school closure policies of varying length [Reference Brown18]. However, in Taiwan, the major efficacy and cost-effectiveness evaluations of control measures against influenza were focused on vaccination [Reference Wang, Wang and Chou19, Reference Wang20]. However, other control measures using engineering approaches [i.e. ventilation, high-efficiency particulate air (HEPA) filtration, and ultraviolet germicidal irradiation (UVGI)], personal protection equipment (i.e. respiratory protection masks), and public health interventions (i.e. isolation and hand washing) were lacking. Thus, it is worthwhile to study the cost-effectiveness analysis of potential control-measure combinations. The control of infectious diseases is often a compromise between the desire for large-scale implementation of control measures and what is logically or economically feasible. The use of cost-effectiveness analysis can help organizations like Medicare to target its healthcare resources more efficiently, and it must be part of a comprehensive strategy [Reference Edmunds, Medley and Nokes21, Reference Neumann, Rosen and Weinstein22]. Cost-effectiveness analysis in healthcare involves the identification of all relevant alternative uses of a resource (cost) in concert with the evaluation of expected health gains derived by implementing that resource.
In this paper, we integrated control-measure modelling as a new dimension of cost-effectiveness analysis to systematically quantify the combinations of control-measure efficacies as well as to understand what is required for seasonal-specific influenza control. Thus, the purpose of this study was to examine the potential health outcomes and cost-effectiveness of different combinations of influenza control strategies in a school setting. The results of this study may be used to maximize health benefits per dollar spent and may be used as an aid to rational public health decision making. Policymakers may need information on the epidemiological and economic impact of different potential control-measure combinations, pertaining to seasonal influenza, in order to formulate tentative guidelines.
MATERIALS AND METHODS
Influenza epidemiology characteristics
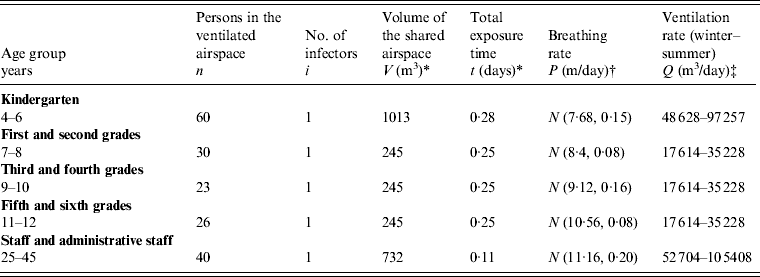
Our study was conducted at Ming-Chuan Elementary School located in southern Taipei. A total of 494 students, including 60 kindergarten and 434 elementary students, were housed in four buildings. The school has two kindergarten classes and 19 elementary classes with grades ranging from 1 to 6. Within those classes, schoolchildren were classified into four age groups: kindergarten (aged 4–6 years) and elementary students (7–8, 9–10, 11–12 years). Teaching and administrative staff aged 25–45 years were also included. Detailed descriptions of the study population have been presented in Chen et al. [Reference Chen, Chang and Liao4]. We adopted the elementary school setting based on weekly seasonal influenza epidemiological data from the Taiwan Center for Disease Control (CDC) databank from 2003 to 2005 (http://www.cdc.gov.tw/en/index.asp). We pooled data into spring/winter and summer/autumn to reflect the seasonal average incidences (Fig. 1a). The estimated spring average incidence rates were 110·94, 57·03, and 72·07/10 000 persons for 2003, 2004, and 2005, respectively; whereas the winter average incidence rates were estimated as 71·78, 53·50, and 71·49/10 000 persons for 2003, 2004, and 2005, respectively (Fig. 1b–d).

Fig. 1 [colour online]. (a) Seasonal influenza epidemiological data from 2003 to 2005 in Taiwan. The number of cases of seasonal influenza are illustrated for winter, spring, summer, and autumn, respectively. (b–d) represents 2003 to 2005 influenza incidence rates in schoolchildren, respectively.
Control measure modelling
Here we used a R 0−θ control curve to formulate the cost-effectiveness analysis, where R 0 represents the basic reproduction number and θ represents the asymptomatic proportion of infected persons. The R 0−θ control curve, denoted as R 0=f(θ), can be derived from an equation-based control model [Reference Chen and Liao5, Reference Fraser23]. Based on the R 0−θ control curve, if a given infectious agent localizes below the curve (area A 1), the outbreak is always controlled eventually; however, if an infectious agent localizes above the curve (area A 2), additional control measures would be required to control spread. The uncontrollable ratio (f uc) used to examine the effectiveness of the control measure adopted can be determined from the R 0=f(θ) curve as (Fig. 2):
where A 1 and A 2 are areas under (representing the controllable area) and above (representing the uncontrollable area) the R 0=f(θ) curve, respectively.

Fig. 2 [colour online]. Illustration of the R 0−θ criteria for outbreak control. The critical line represents the combination of R 0, θ, and certain efficacies of control measures that can be shown in equations (T3)–(T5) (Table 1).
Table 1 summarizes the mathematical models used to calculate R 0 with and without control measures and R 0=f(θ) functions based on different public health interventions. The proposed control measures included engineering approaches such as natural ventilation (G), high-efficiency particulate air (HEPA, H) filtration, and ultraviolet germicidal irradiation (UVGI, U) and personal protection equipment such as utilization of respiratory protection masks (M). The public health interventions were isolation (I), vaccination (V), and hand washing (HW).
Table 1. Mathematical expressions for basic reproduction number (R0) without control measures, with engineering and personal protection control measures, and R0=f( θ ) functions with i public health interventions and personal control measures

n is the population size; I is the number of infectors; q is the quantum generation rate by an infected person (quanta/day); p is the breathing rate per person (m3/day); t is the total exposure time (days); Q is the fresh air supply rate (m3/day); V is the volume of the ventilated space (m3); Q r is the air flow rate through a recirculation HEPA filter (m3/h); η δ is the efficiency of respiratory protection masking used by an infected person (dimensionless); η r is the single-pass removal efficiency for an infectious droplet nuclei passing through the recirculation HEPA filter (dimensionless); ACH is the air change rate (/h); ACH r is the air change rate through a recirculation HEPA filter (/h); λ is the inactivation rate of an infectious droplet nuclei due to UVGI (/h); and ε 1, ε 2, and ε 3 denote the efficacies of isolation, vaccination, and hand washing, respectively.
Parameter estimates for θ can be determined by the specific biological characteristics of the aetiological agents, where θ= (incubation period−latent period)/infectious period. We calculated the distribution of θ using the Monte Carlo simulation to quantify the uncertainty concerning θ, which was attributable to the large variance of the incubation, latent, and infectious periods for a specific airborne infection. Utilizing previous work, we were able to obtain range values for the incubation, latent, and infectious periods as 1–4, 1–3, and 4–8 days, respectively, for influenza [Reference Anderson and May8].
Unit cost estimations
Table 2 summarizes the unit cost per year for engineering control measures, personal protection, and public health interventions. The costs of outpatient treatment were estimated to be US$11.55 per person [Reference Neumann, Rosen and Weinstein22]. The costs of UVGI were separated into equipment (lamp) and consumption (UV) costs. The lifespan of one lamp was estimated to be around 8000–10 000 hours; hence, the costs of UVGI per year were estimated to be US$182. The costs of HEPA filtration were also separated into equipment and consumption costs based on the available market price, resulting in a consumption cost estimated at US$137 per year.
Table 2. Unit cost of control measures including engineering, personal protection, and public health interventions

UVGI, Ultraviolet germicidal irradiation; HEPA, high-efficiency particulate air; NT$, New Taiwan dollar.
Average exchange rates between NT$ and US$ in March 2007. (https://ebank.bot.com.tw).
The costs of isolation per year were reasonably assumed to be US$3040 based on expert opinion. The costs of inactivated influenza vaccination per year were estimated by the cost of one vaccine (US$12.50) plus the administrative fee (US$6.25), resulting in a cost of US$18.75 per person [Reference Edmunds, Medley and Nokes21]. The costs of respiratory masking (i.e. using surgical masks) were estimated to be US$27.36 per year based on the 60 masks used per year at Ming-Chung Elementary School. The costs of hand washing were calculated to be US$1605 per year, which was estimated based on the advertised cost of US$1520 plus the cost of water consumption. Detailed descriptions are listed in Table 2.
Cost-effectiveness analysis
Our proposed cost-effectiveness analyses involved four scenarios. Scenario 1 represented no control measures. Scenario 2 represented a combination of engineering approaches and personal protection equipment. Our costs only reflected the outpatient treatment costs due to a lack of information in the questionnaire and other related information such as the costs associated with work loss. Scenario 3 involved a combination of public health interventions and personal protection equipment. Scenario 4 represented several engineering approaches and public health interventions associated with personal protection. Detailed descriptions of the cost estimation for scenarios 1–4 are presented in Appendix 2. Finally, the cost-effectiveness analysis tended to quantify the unit cost per person per year. In other words, we used average cost burden per year divided by all populations (in units of US$/year per person) in order to evaluate the optimal control measures.
RESULTS
Estimates of basic reproduction number
A Wells–Riley mathematical model [equation (T1), Table 1] of indoor respiratory infection [Reference Liao, Chang and Liang3–Reference Chen and Liao5] was employed to estimate the exposure concentrations (q) in indoor environments and to estimate the basic reproduction number (R 0) in a shared indoor airspace. The exposure concentrations (q) were calculated with input parameters of N = 50, V = 600 m3, t = 6 h, P = 0·38 m3/h, f = 0·00119, I = 1, P = LN (0·0073, 1·22) and LN (0·0048, 1·44) for winter and summer, respectively (Table 3). The Monte Carlo simulation results show the best fitted lognormal distributions of q with geometric means of 33·92 and 51·62 and geometric standard deviations of 1·14 and 1·22 for summer and winter, respectively.
Table 3. Input parameters used in the Wells–Riley mathematical equation for five age groups in an elementary school

* Estimated from the measurement and course programme at Ming-Chuan Elementary School.
† Adopted from ICRP [30].
‡ Assuming that the ACH = 2–3/h and 4–6/h for kindergarten students and other age groups, respectively.
The box-and-whisker plots of the median basic reproduction numbers (R 0) were estimated to be 3·22, 2·14, 1·71, 2·15, 2·85 for summer and 7·32, 3·78, 4·30, 5·43, 5·98 for winter, respectively, for the five age groups at Ming-Chuan Elementary School (Fig. 3a, b). Figure 3(c, d) shows the median risks of infection (P) in the five age groups for summer and winter, respectively. Grades 5 and 6 gave the highest risk of infection for all seasons. Kindergarten had the highest R 0 estimates, implicating that the density of the population affects age group-specific R 0.

Fig. 3 [colour online]. (a, b) Box-and-whisker plots of the seasonal basic reproduction number (R 0) and (c, d) risk of infection (P) for summer and winter, respectively. Five age groups, including kindergarten, grades 1–2, 3–4, and 5–6, and staff/administrative staff, respectively, are defined.
Predicting the effects of engineering and personal protection
We used equation (T2) (Table 1) to calculate the basic reproduction number (R 0E) under multiple engineering and personal protection control measures. We inputted the inactivation rate of infectious droplets due to UVGI (λ = 12/h) [Reference Beggs24], single-pass removal efficiency for infectious droplet nuclei passing through the recirculation HEPA filter (η r = 99·97%), and air change rate through a recirculation HEPA filter (Q r = 3·499 m3/h) into equation (T2).
The effects of engineering and personal protection are shown in Figure 4. For one control measure (G, natural ventilation) in winter, the median R 0E estimates notably decreased from 7·32, 4·5, and 5·98 (Fig. 3b) to 1·35, 2·11, and 1·33 (Fig. 4b) for kindergarten, elementary, and staff and administrative staff, respectively. For two control measures, it produced an order of G+U > G+M > G+H. Finally, using combinations of G+M+H, G+M+U, and G+H+U produced an order of efficacy of G+M+U > G+H+U > G+M+H (Fig. 4).

Fig. 4 [colour online]. Under multiple control measures of natural ventilation (G), respiratory masking (M), ultraviolet germicidal irradiation (UVGI, U), and high-efficiency particulate air (HEPA, H) filtration, estimates of seasonal R 0E were produced and are shown for (a) summer and (b) winter. Three age groups of kindergarten, elementary students, and staff/administrative staff are included.
Effectiveness of public health interventions and personal protection
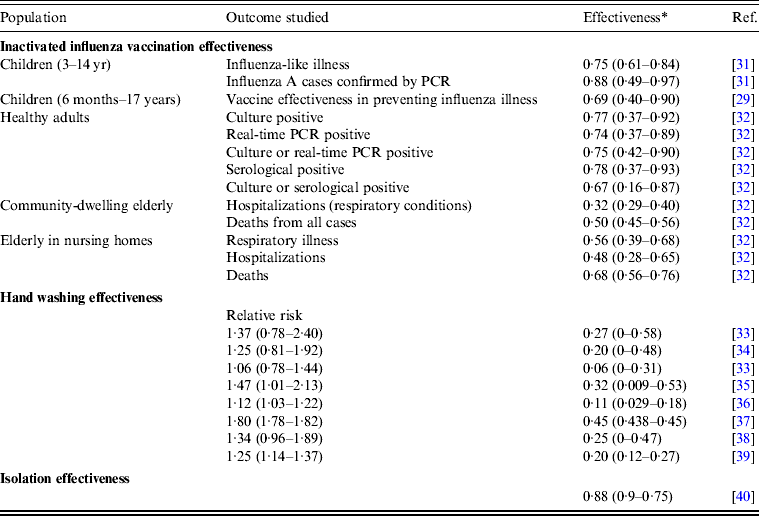
Table 4 summarizes the available published effectiveness data for inactivated influenza vaccination (V), hand washing (HW), and isolation (I). We deduced that the average vaccination effectiveness estimates were 0·70, 0·62, and 0·50 with standard deviations of 0·06, 0·06, and 0·03 for children, adults, and the elderly, respectively, by using 10 000 Monte Carlo simulations. On the other hand, the average effectiveness of hand washing and isolation were estimated to be 0·24 and 0·82 with standard deviations of 0·03 and 0·06, respectively.
Table 4. Published effectiveness (median with 95% confidence interval) of selected public health interventions of vaccination, hand washing, and isolation

PCR, Polymerase chain reaction.
* Effectiveness = 1 – (1/relative risks) × 100% [Reference Jefferson40].
The impact of the different combinations of public health interventions (V, HW, I) were assessed by R 0−θ control models [equations (T3)–(T5)] (Table 1). Parameter estimates for θ of influenza were determined by the specific biological characteristics of the aetiological agents. The uniform distributions [represented as mean (min-max)] that best fit the incubation, latent, and infectious periods were estimated to be 2·5 (1·0–4·0), 2·0 (1·0–3·0), and 6·0 (4·0–8·0) days, respectively. In the uniform distribution, all values between the minimum and maximum occur with equal likelihood. Hence, we assumed the ranges were minimum and maximum and all values between the minimum and maximum occur with equal likelihood. The 95% confidence intervals (CIs) for the proportion of people with asymptomatic infection ranged from 0·19 to 0·44 by the definition of θ. Finally, Figure 5 shows that the effectiveness of public health intervention followed the order of I > V > HW and I+V > I+HW > V+HW across all age groups, indicating that isolation had the greatest effect on influenza control without considering the cost effects.

Fig. 5 [colour online]. Modelling the impact of the combinations of public health intervention and personal protection, including isolation (I), vaccination (V), and hand washing (HW). Panels (a)–(e) represent the five age groups of the R 0−θ critical control model based on I, V, HW, I+V, I+HW, V+HW, and I+V+HW in winter and associated with the estimates of the basic reproduction number (R 0) and the proportion of asymptomatic infection (θ).
Cost-effectiveness analysis
Cost-effectiveness analysis for scenario 1 is presented in Figure 6(a, b). The box-and-whisker plots without any control measures in summer show that the average cost for a kindergarten student was US$2.64/year per person (95% CI 2·39–2·84), indicating that the costs are higher than those of elementary students (US$1.40/year per person; 95% CI 1·00–1·85) and teaching and administrative staff (US$2.32/year per person; 95% CI 2·23–2·40) (Fig. 6a). Similarly, the costs for kindergarten students in winter (US$4.5/year per person; 95% CI 4·23–4·77) were also higher than those of elementary students (US$3.4/yr per person; 95% CI 2·69–4·13) and teaching and administrative staff (US$4.13/year per person; 95% CI 4·01–4·27) (Fig. 6b). The costs in winter were 41% higher than in summer for the kindergarten age group.

Fig. 6 [colour online]. (a, b) Cost-effectiveness analyses for scenario 1 (without any control measures) for the three age groups of kindergarten, elementary, and staff/administrative staff. (c, d) Cost-effectiveness analysis for scenario 2 (multiple engineering and personal protection control measures) are presented.
Cost-effectiveness analysis for scenario 2 was estimated to be US$0.67 (G+M), US$3.23 (G+U), and US$3.92/year per person (G+H) for kindergarten students (Fig. 6c). Costs in winter were 68%, 10%, and 30% higher than those in summer for kindergarten students for the G+M, G+U, and G+H combinations, respectively (Fig. 6d). For cost-effectiveness analysis in scenario 3, the results showed that US$31.25/year per person for hand washing was the highest cost-effectiveness control measure compared to isolation (US$55.16/year per person) and vaccination (US$85.75/year per person) (Fig. 7).

Fig. 7 [colour online]. (a) Cost-effectiveness analysis for scenario 3 (multiple public health intervention and personal protection control measures) in summer and winter for the three age groups, respectively.
DISCUSSION
This study attempted to examine the potential health outcomes and cost-effectiveness of different combinations of influenza control strategies in a school setting. This information may be useful to maximize the health benefits per dollar spent and can be used as an aid to rational public health decision making.
We found a set of intervention strategies that gave the highest reduction in basic reproductive number. For multiple engineering approaches and personal control measures, G+M+H+U strategies were the most effective interventions with a corresponding R 0E estimate of 0·22 (95% CI 0·15–0·33) for kindergarten students in winter. G+U and G+M+U strategies had an R 0E estimation of 0·45 (95% CI 0·30–0·66) and 0·22 (95% CI 0·15–0·33), respectively (Fig. 4b). For multiple public health interventions, the R 0 estimates for kindergarten students in winter decreased to 6·88 (95% CI 5·98–8·12), 7·19 (95% CI 6·25–8·49), and 7·32 (95% CI 6·36–8·64) for I+V+HW, I+V, and I+HW, respectively [equations (T3)–(T5)]. Regarding our dynamic transmission model and economic evaluation, this study indicated that the optimal cost-effective strategy for all scenarios was the combination of natural ventilation and respiratory masking. The estimated costs were US$10/year per person in winter for one kindergarten student. The cost for hand washing was estimated to be US$32/year per person, which was much lower than isolation (US$55/year per person) and vaccination (US$86/year per person) costs in containing seasonal influenza.
The main strength of this study was that it provides a new perspective on methods to integrate the maximum estimation for infected numbers of people, unit cost of outpatients, and cost estimations of control measures. We used the R 0=f(θ) function to describe the control impact on the basic reproduction number (R 0) through the use of isolation, vaccination, and hand washing. This study also simulated engineering approaches (using HEPA filtration and UVGI) and respiratory protection masking in a school setting by use of a modified Wells–Riley equation. Most cost-effectiveness studies are focused on vaccination of high-risk populations, including the elderly [Reference Edmunds, Medley and Nokes21, Reference Maciosek25–Reference Hoshi27] and children [Reference Weycker28, Reference Prosser29], because many countries have an established Medicare system, and hospital databases that can offer methods to evaluate the (in)direct costs when influenza vaccination is adopted. Many of these studies did not consider the effects of engineering approaches or respiratory protection masking on cost-effectiveness analysis for influenza epidemics. For seasonal-specific analysis, results indicate that it was not possible to provide an exact prediction of cost-effectiveness because several model inputs were uncertain. For example, the frequency of hand washing in 1 day or the cost per 1 litre of water was variable. Other model inputs such as the replacement frequency of respiratory masks and the types of masks used were different. There are two limitations to our study. A potential weakness of the analysis was that it only considered the costs of outpatient treatment for people who became infected. The indirect costs for work and productivity loss, even the hospitalization costs that arise from illness, were not taken into account. Hence, the burden of disease could be underestimated in our study. In other words, the total costs for each scenario were largely derived from the costs of control measures and not the costs of outpatient treatment. The second potential weakness of our study is that engineering methods may not be feasible. Natural ventilation represents a cost-effective approach; however, the ventilation conditions were not easy to quantitate and adjust.
In conclusion, this study provides important baseline information on the costs and effectiveness of control strategies that can be used to judge the overall impact of communicable disease on the health of the population. For seasonal-specific cost-effectiveness analysis, the cost in winter was slightly higher than in summer, implying that we need more efforts on school health promotion programmes in the winter season. Our study also demonstrates that model-based, cost-effectiveness analysis can be useful to explore infectious disease trends and health consequences of interventions in a population over time, providing insight into the impacts of economic factors and health benefits on certain prevention combinations against seasonal influenza transmission. In the future, cost-effectiveness analysis must be part of a comprehensive strategy that involves changing incentives at multiple levels.
APPENDIX 1. The SEIR model
The parameters S, E, I, and R were used for the epidemiological classes. The SEIR model can provide a basic description of the transmission dynamics of pandemic influenza by using a simple parameterized set of ordinary differential equations:
where N(t), S(t), E(t), I(t), and R(t) represent the number of total persons, susceptible, exposed, infected, and recovered at time t for specific age groups, respectively. β represents the transmission coefficient for the probability that an infected person will have contact with and successfully infect a susceptible person, which can be estimated by R 0=(β × N)/(μ+ν) [Reference Anderson and May8]. σ represents the rate at which an exposed individual becomes infectious per unit time, which is equal to 0·333/day [Reference Anderson and May8]. υ represents the rate at which an infectious individual recovers per unit time (per day) and is equal to 0·143 (1/average infectiousness periods of 7 days). μ represents the birth rate and death rate, which is equal to 0·013/year (http://www.mio.gov.tw/stat/).
APPENDIX 2. Cost estimations for scenarios 1–4
The costs (in US$/year per person) for scenario 1 (costWC) and scenario 2 (costEC) are represented as:
where I max–WC and I max–EC represent the maximum infected number of people without intervention and with intervention (engineering and personal protection control), respectively. C f represents the unit cost per person of the outpatient treatment. C EC represents the cost associated with the combination of engineering and personal protection control strategies. The estimated basic reproduction numbers in scenarios 1 and 2 are respectively denoted as R 0 and R 0E. A classic SEIR model (see Appendix 1) can be used to estimate the maximum infected number in a population (I max).
The costs in scenarios 3 and 4 are given as:
where I max–PI is the maximum infected number of people with intervention (public health interventions and personal protection strategies). C PI represents the cost of specific public health interventions and personal protection in a population. For scenario 3, R 0 estimates can be obtained based on R 0=f(θ) functions as varied with different public health interventions and personal protection as: R 0 × f uc. For scenario 4, the total costs of control measure combinations (costPE) are given in equation (A9). The I max–PE is the maximum infected number of people with intervention (public health interventions and the combination of engineering and personal protection controls). R 0 estimates can then be estimated from R 0E × f uc.
DECLARATION OF INTEREST
None.