Impact Statement
This paper addresses the challenge of developing universally transferable hydrological modeling approaches using machine learning by investigating the feature space and demonstrating the case for more ubiquitous physics-based proxy variables. The authors propose an approach that utilizes only meteorological variables to force a streamflow model with proxies for measurements of internal mechanics without a loss of predictive performance. Such an approach could enable more effective general hydrological machine learning models to assess climate change impact on global hydrological systems.
1. Introduction
Artificial neural aetworks (ANNs) in various forms have been studied in hydrology over a significant period of time with a high level of model skill in many cases (Aichouri et al., Reference Aichouri, Hani, Bougherira, Djabri, Chaffai and Lallahem2015; Ali and Shahbaz, Reference Ali and Shahbaz2020; ASCE Task Committee on Application of Artificial Neural Networks in Hydrology, 2000; Ayzel and Heistermann, Reference Ayzel and Heistermann2021; Dawson et al., Reference Dawson, Abrahart, Shamseldin and Wilby2006; Gao et al., Reference Gao, Huang, Zhang, Han, Wang, Zhang and Lin2020; Govindaraju et al., Reference Govindaraju, Ramachandra Rao and Singh2000; Kumar et al., Reference Kumar, Raju and Sathish2004). However, they have not been widely taken up for operational use, perhaps due to the perceived lack of interpretability of model mechanics, and a lack of consistency in data frameworks and model specification (Abrahart et al., Reference Abrahart, Anctil, Coulibaly, Dawson, Mount, See, Shamseldin, Solomatine, Toth and Wilby2012). When compared with established mechanistic models, such as the Système Hydrologique Européen (SHE) (Abbott et al., Reference Abbott, Bathurst, Cunge, O’Connell and Rasmussen1986a, Reference Abbott, Bathurst, Cunge, O’Connell and Rasmussen1986b) or the Soil and Water Assessment Tool (SWAT) (Arnold et al., Reference Arnold, Srinivasan, Muttiah and Williams1998; Srinivasan et al., Reference Srinivasan, Ramanarayanan, Arnold and Bednarz1998), which have been used extensively (Refsgaard et al., Reference Refsgaard, Storm and Clausen2010), there is no widely accepted machine learning framework, despite the relative maturity of the algorithms themselves.
Mechanistic methods requiring extensive calibration and large amounts of hydromorphological data (Devi et al., Reference Devi, Ganasri and Dwarakish2015; Jaiswal et al., Reference Jaiswal, Ali and Bharti2020) can, therefore, be difficult to apply globally. This is partly due to the inequity of meteorological and hydrological data collection (Kidd et al., Reference Kidd, Becker, Huffman, Muller, Joe, Skofronick-Jackson and Kirschbaum2017; Krabbenhoft et al., Reference Krabbenhoft, Allen, Lin, Godsey, Allen, Burrows, DelVecchia, Fritz, Shanafield, Burgin, Zimmer, Datry, Dodds, Jones, Mims, Franklin, Hammond, Zipper, Ward, Costigan, Beck and Olden2022) (many flood events have little or no observational data associated with them (Robson and Reed, Reference Robson and Reed2008)), but looking to the future, climate nonstationarity driven by anthropogenic climate change (Wilby and Quinn, Reference Wilby and Quinn2013) could cause issues in precalibrated models. However, we might perhaps learn patterns from areas of extensive measurement and extrapolate toward those without. It is in this case that machine learning might be best applied (Bishop, Reference Bishop2016).
On other empirical methods, such as those described in the Flood Estimation Handbook (Calver et al., Reference Calver, Stewart and Goodsell2009; Faulkner et al., Reference Faulkner, Francis and Lamb2012; Institute of Hydrology, 2008; Samuels et al., Reference Samuels, Huntington, Allsop and Harrop2008), our concern is that their utility may diminish in the face of the aforementioned nonstationarity, which may cause a shift in flood event distributions through an increase in the frequency of extreme events, and the tighter demands that might be expected of predictions in response to climate change.
If data availability is a problem for many locations, we might wish to rule out approaches that use measurements of internal processes within a catchment. This could rule out the application of autoregressive approaches that require prior knowledge of runoff or flow values (Aichouri et al., Reference Aichouri, Hani, Bougherira, Djabri, Chaffai and Lallahem2015; Ali and Shahbaz, Reference Ali and Shahbaz2020). In this work, we posit that “external” measurements (those that do not require direct observation inside a catchment, for example, gridded output from a meteorological model) are the only ones that we can assume reliably available, making our adopted position an approach that has to be an input–output model but still explainable.
To achieve this, we aim to find a way to represent the internal state of a catchment, in terms of water storage as soil moisture, using more easily attainable “external” variables. The representation of internal soil moisture state we will approximate through statistical parameterizations of the histories of meteorological variables, resulting in what we term antecedent proxies. We use these antecedent proxies to force the machine learning model alongside the other input variables and compare to outputs from a model of the same architecture that takes soil moisture as input instead of the proxies. We hope that this highlights how machine learning models can be used to reframe a problem while remaining faithful to the established understanding of science in the field.
Our goal, therefore, is to lay a foundation for maximizing the generalization capability (in terms of region of applicability) of hydrological machine learning models by minimizing the data burden. We have three objectives. First, we aim to create a model that responds only to “external” climatic variables (those that can be accessed without measurement within the catchment). Second, we aim for model parsimony by balancing the number of input variables against model skill. We base this on the premise that using fewer variables leads to a more explainable model and one that is easier to apply. Third, our variable choices must be physically reasoned. This is particularly true of the proxy variables that we choose to represent those internal processes of a catchment that we do not observe.
2. Theory and methods
2.1. Catchment conceptualization
In terms of the inputs and outputs that will form the basis of a machine learning model, we consider a crude representation of an inland catchment, one we assume is not affected by tidal inflows, with water entering the catchment through precipitation and exiting through evaporation, transpiration, and through the streamflow outflow, our target variable. We think of the internal processes as ones that move water toward one of the outflow processes or into internal storage.
More formally, the sum total of water that leaves a catchment via river discharge, that enters or leaves through climatic, or other, processes, and any changes to water stored within a catchment must be equal to zero, as per the integral form of continuity in Equation (2.1)) (Yilmaz et al., Reference Yilmaz, Gupta and Wagener2008), where the cumulative precipitation over a time period with length
![]() $ T $
in the catchment is given by
$ T $
in the catchment is given by
![]() $ {\int}_{t=0}^T{\Psi}_t dt $
, the water leaving the catchment through evapotranspiration is
$ {\int}_{t=0}^T{\Psi}_t dt $
, the water leaving the catchment through evapotranspiration is
![]() $ {\int}_{t=0}^T Edt $
, the target streamflow exiting through the river is
$ {\int}_{t=0}^T Edt $
, the target streamflow exiting through the river is
![]() $ \therefore {\int}_{t=0}^T{Y}_t $
, and the change in water storage is
$ \therefore {\int}_{t=0}^T{Y}_t $
, and the change in water storage is
![]() $ \Delta S $
.
$ \Delta S $
.
 $$ {\displaystyle \begin{array}{l}\hskip6em 0=\int_{t=0}^T{\Psi}_t dt-\int_{t=0}^T{Y}_t dt-\int_{t=0}^T Edt-\Delta S\\ {}\therefore \int_{t=0}^T{Y}_t dt=\int_{t=0}^T{\Psi}_t dt-\int_{t=0}^T Edt-\Delta S\end{array}} $$
$$ {\displaystyle \begin{array}{l}\hskip6em 0=\int_{t=0}^T{\Psi}_t dt-\int_{t=0}^T{Y}_t dt-\int_{t=0}^T Edt-\Delta S\\ {}\therefore \int_{t=0}^T{Y}_t dt=\int_{t=0}^T{\Psi}_t dt-\int_{t=0}^T Edt-\Delta S\end{array}} $$
We further simplify the hydrological system by considering the meteorological inputs and outputs as acting at a single point, rather than being spatially distributed. This single point we take is the center of the catchment, or, more concretely, the centroid of the catchment, being the geometric center of a catchment’s two-dimensional surface, equivalent to its center of mass for a congruent shape of uniform weight density. Assuming that a catchment is a shape in two dimensions with area,
![]() $ A $
, its centroid, with coordinates
$ A $
, its centroid, with coordinates
![]() $ \left(\overline{x},\overline{y}\right) $
, is given by taking first moments of area in both axes, with respect to some frame of reference, divided by the shape’s area, as in Equation (2.2)):
$ \left(\overline{x},\overline{y}\right) $
, is given by taking first moments of area in both axes, with respect to some frame of reference, divided by the shape’s area, as in Equation (2.2)):
 $$ \overline{x}=\frac{\int_Ax\; dA}{\int_A dA};\hskip1em \overline{y}=\frac{\int_Ay\; dA}{\int_A dA} $$
$$ \overline{x}=\frac{\int_Ax\; dA}{\int_A dA};\hskip1em \overline{y}=\frac{\int_Ay\; dA}{\int_A dA} $$
where, for the purposes of this calculation, we will consider the catchment as a surface that exists in a flat, two-dimensional plane, effectively removing elevation and reducing the dimensionality of its boundary,
![]() $ B $
, such that
$ B $
, such that
![]() $ B\in {\mathrm{\mathbb{R}}}^2 $
rather than
$ B\in {\mathrm{\mathbb{R}}}^2 $
rather than
![]() $ B\in {\mathrm{\mathbb{R}}}^3 $
and treating that boundary as the continuous edge of an irregular shape with uniform density.
$ B\in {\mathrm{\mathbb{R}}}^3 $
and treating that boundary as the continuous edge of an irregular shape with uniform density.
As we focus on catchment-specific models, we therefore do not use catchment descriptors as inputs. The predicted flow dynamics are dependent in a nonlinear way on the contemporaneous catchment descriptors, rather than stationary catchment descriptors, and the precipitation response function is not constant; rather, it is learned as a function of the antecedent conditions, captured through soil moisture or its proxies. Furthermore, many catchment descriptors within the United Kingdom are relatively stable; for example, the total amount of agricultural land, representing 72.8% of the UK’s total land cover, only varied by 1.3% in a 30-year period from 1990 to 2020 (Department for Environment, Food, and Rural Affairs, 2024; Department for Levelling Up, Housing and Communities, 2023).
2.2. Artificial neural networks
2.2.1. Overview
The multilayer perceptron (MLP) is composed of multiple, interconnected neuron units, each combining inputs linearly before an activation function is applied; depending on the choice for that activation function, nonlinearity can be introduced. A single neuron along the structure for an arbitrary MLP is shown in Figure 1, where the output,
![]() $ y $
, from a single neuron with respect to its inputs,
$ y $
, from a single neuron with respect to its inputs,
![]() $ \mathbf{x} $
, is a general linear combination of those inputs, with weights
$ \mathbf{x} $
, is a general linear combination of those inputs, with weights
![]() $ \mathbf{w} $
and bias
$ \mathbf{w} $
and bias
![]() $ b $
, prior to the activation function,
$ b $
, prior to the activation function,
![]() $ \alpha $
, being applied.
$ \alpha $
, being applied.
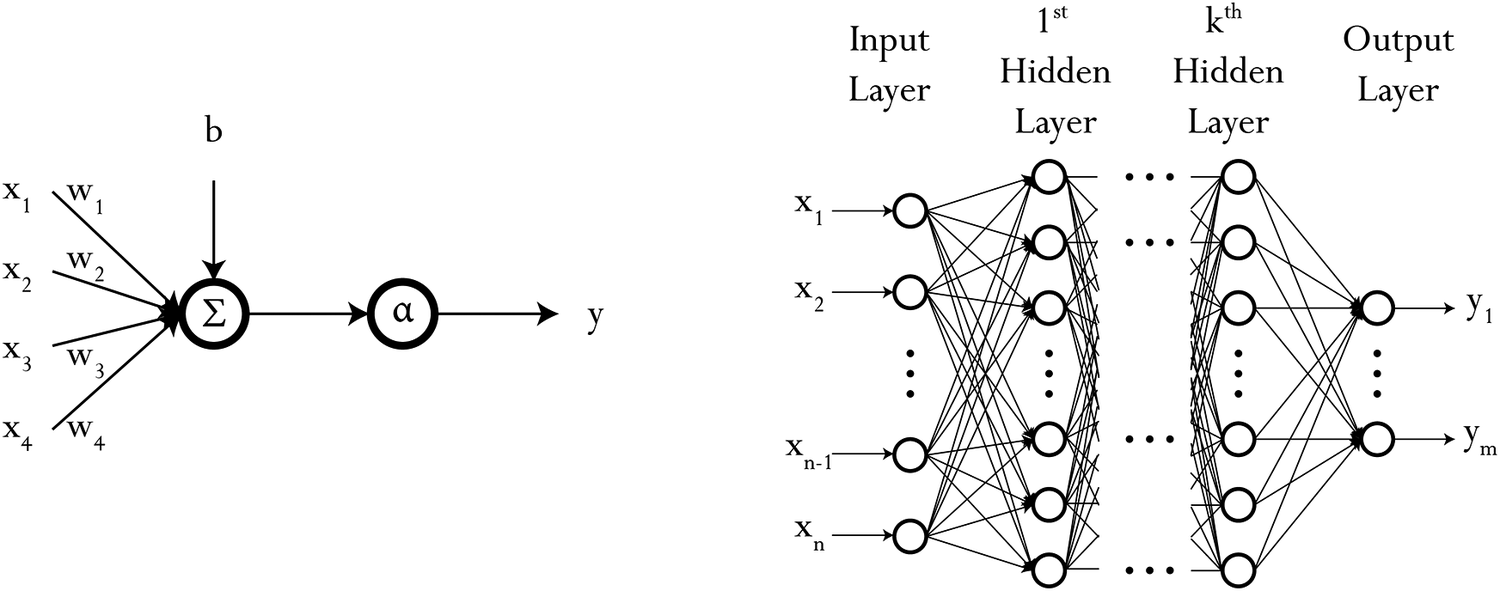
Figure 1. Graphical representation of a single neuron unit and an arbitrary neural network with
![]() $ l $
layers.
$ l $
layers.
If we let
![]() $ \Phi $
represent the set of all parameters to be learned, then we can use the difference between a prediction made with the network,
$ \Phi $
represent the set of all parameters to be learned, then we can use the difference between a prediction made with the network,
![]() $ {y}^{\prime } $
, and the target value,
$ {y}^{\prime } $
, and the target value,
![]() $ y $
, through a cost function,
$ y $
, through a cost function,
![]() $ J\left(\Phi \right) $
, such as the root-mean-squared error (RMSE) form in Equation 2.3.
$ J\left(\Phi \right) $
, such as the root-mean-squared error (RMSE) form in Equation 2.3.
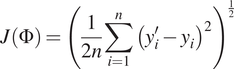 $$ J\left(\Phi \right)={\left(\frac{1}{2n}\sum \limits_{i=1}^n{\left({y}_i^{\prime }-{y}_i\right)}^2\right)}^{\frac{1}{2}} $$
$$ J\left(\Phi \right)={\left(\frac{1}{2n}\sum \limits_{i=1}^n{\left({y}_i^{\prime }-{y}_i\right)}^2\right)}^{\frac{1}{2}} $$
To minimize the value of the cost function, with respect to the parameters
![]() $ \Phi $
, we typically use gradient descent to update each parameter,
$ \Phi $
, we typically use gradient descent to update each parameter,
![]() $ {\phi}_j $
, according to the sign and magnitude of the gradient, controlled by the learning rate hyperparameter
$ {\phi}_j $
, according to the sign and magnitude of the gradient, controlled by the learning rate hyperparameter
![]() $ \eta $
, as per Equation 2.4.
$ \eta $
, as per Equation 2.4.
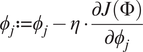 $$ {\phi}_j:= {\phi}_j-\eta \cdot \frac{\partial J\left(\Phi \right)}{\partial {\phi}_j} $$
$$ {\phi}_j:= {\phi}_j-\eta \cdot \frac{\partial J\left(\Phi \right)}{\partial {\phi}_j} $$
The Backpropagation algorithm (Rumelhart et al., Reference Rumelhart, Hinton and Williams1986) enables the application of gradient descent in networks by propagating the derivatives backward between layers; for the parameters at the
![]() $ {l}^{th} $
layer of a network with
$ {l}^{th} $
layer of a network with
![]() $ L $
layers, the update gradient for that layer is chained back through all previous layers and activation functions,
$ L $
layers, the update gradient for that layer is chained back through all previous layers and activation functions,
![]() $ {\alpha}_L,\dots, {\alpha}_l $
, as in Equation 2.5.
$ {\alpha}_L,\dots, {\alpha}_l $
, as in Equation 2.5.
2.2.2. Implementation
The model we define here is applied individually to each catchment: instances of the model learn from and predict for each catchment separately. The MLP structure is relatively simple, comprising only two hidden layers with unitary output, where the number of nodes in the first hidden layer is half the dimension of the input space and the number of nodes in the second hidden layer is halved again. The activation function is the sigmoid linear unit (Ramachandran et al., Reference Ramachandran, Zoph and Le2017), and the optimization algorithm we use is the Adam algorithm, its name coming from adaptive moment estimation (Kingma and Ba, Reference Kingma and Ba2017; Ruder, Reference Ruder2017). Inputs to the model are also normalized, using values from the training set only, to smooth training.
An advantage of MLPs is that they offer a simple baseline neural network that, as a universal function approximator, is still capable of learning complex nonlinear relationships. Given that MLPs have demonstrated high predictive skill in extensive application to hydrological problems (Aichouri et al., Reference Aichouri, Hani, Bougherira, Djabri, Chaffai and Lallahem2015; Ali and Shahbaz, Reference Ali and Shahbaz2020; ASCE Task Committee on Application of Artificial Neural Networks in Hydrology, 2000; Ayzel and Heistermann, Reference Ayzel and Heistermann2021; Dawson et al., Reference Dawson, Abrahart, Shamseldin and Wilby2006; Gao et al., Reference Gao, Huang, Zhang, Han, Wang, Zhang and Lin2020; Govindaraju et al., Reference Govindaraju, Ramachandra Rao and Singh2000; Kumar et al., Reference Kumar, Raju and Sathish2004), this learning capability includes the relationship between the catchment state and the response to precipitative forcing. Furthermore, extracting the sensitivity of the model to individual variables is a straightforward process that enables the analysis of the relative importance of each variable.
2.3. Error metrics
To assess the performance of the equation, we employ the following metrics: RMSE, expressed in Equation 2.6; mean percent relative error (MPRE), expressed in Equation 2.7; relative bias (RB), expressed in Equation 2.8; Nash-Sutcliffe efficiency (NSE), expressed in Equation 2.9; and Kling-Gupta efficiency (KGE), expressed in Equation 2.10. The RMSE and MPRE both give an indication of the absolute magnitude of the absolute error and, accordingly, have a range of
![]() $ \left[0,\infty \right) $
, where
$ \left[0,\infty \right) $
, where
![]() $ 0 $
indicates a perfect score. RB, on the other hand, identifies whether or not a model is on average under- or overpredicting and has a range of
$ 0 $
indicates a perfect score. RB, on the other hand, identifies whether or not a model is on average under- or overpredicting and has a range of
![]() $ \left(-\infty, \infty \right] $
. NSE and KGE, through normalization, enable the model’s accuracy to be compared across catchments more easily and are commonly used in hydrology to do so (Gupta et al., Reference Gupta, Kling, Yilmaz and Martinez2009; Nash and Sutcliffe, Reference Nash and Sutcliffe1970), each with a range of
$ \left(-\infty, \infty \right] $
. NSE and KGE, through normalization, enable the model’s accuracy to be compared across catchments more easily and are commonly used in hydrology to do so (Gupta et al., Reference Gupta, Kling, Yilmaz and Martinez2009; Nash and Sutcliffe, Reference Nash and Sutcliffe1970), each with a range of
![]() $ \left(-\infty, 1\right] $
. While both metrics provide a sense of how the model is performing compared to the mean, where an NSE of 0 and a KGE of −0.41 would indicate performance equivalent to the mean flow benchmark (Wouter et al., Reference Wouter, Knoben, Freer and Woods2019), KGE is intended to capture the discrepancy between the variability and timing of the compared datasets. While obtaining a score of 1
$ \left(-\infty, 1\right] $
. While both metrics provide a sense of how the model is performing compared to the mean, where an NSE of 0 and a KGE of −0.41 would indicate performance equivalent to the mean flow benchmark (Wouter et al., Reference Wouter, Knoben, Freer and Woods2019), KGE is intended to capture the discrepancy between the variability and timing of the compared datasets. While obtaining a score of 1
![]() $ 1 $
for the NSE and KGE would be ideal, obtaining scores of NSE
$ 1 $
for the NSE and KGE would be ideal, obtaining scores of NSE
![]() $ \ge 0.5 $
(Moriasi et al., Reference Moriasi, Arnold, Van Liew, Bingner, Harmel and Veith2007) and KGE
$ \ge 0.5 $
(Moriasi et al., Reference Moriasi, Arnold, Van Liew, Bingner, Harmel and Veith2007) and KGE
![]() $ \ge 0.5 $
(Rogelis et al., Reference Rogelis, Werner, Obregón and Wright2016) are thresholds of suitable model performance.
$ \ge 0.5 $
(Rogelis et al., Reference Rogelis, Werner, Obregón and Wright2016) are thresholds of suitable model performance.


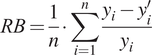

 $$ KGE=1-\sqrt{{\left(r-1\right)}^2+{\left(\frac{{\overline{y}}^{\prime }}{\overline{y}}-1\right)}^2+{\left(\frac{\sigma_{y^{\prime }}}{\sigma_y}-1\right)}^2} $$
$$ KGE=1-\sqrt{{\left(r-1\right)}^2+{\left(\frac{{\overline{y}}^{\prime }}{\overline{y}}-1\right)}^2+{\left(\frac{\sigma_{y^{\prime }}}{\sigma_y}-1\right)}^2} $$
All of these metrics are expressed in terms of the
![]() $ n $
pairwise observations,
$ n $
pairwise observations,
![]() $ {y}_i $
, and model predictions,
$ {y}_i $
, and model predictions,
![]() , with the KGE also relying on the use of the linear correlation between observations and simulations,
, with the KGE also relying on the use of the linear correlation between observations and simulations,
![]() $ r $
, and the standard deviation of predictions,
$ r $
, and the standard deviation of predictions,
![]() $ {\sigma}_{y^{\prime }} $
, and observations,
$ {\sigma}_{y^{\prime }} $
, and observations,
![]() $ {\sigma}_y $
.
$ {\sigma}_y $
.
2.4. Sensitivity and comparative analysis
To make a comparison of the impact that the soil moisture and antecedent proxy variables have, we utilize an additional pair of methodologies. The first is the correlation between variables, specifically the Pearson Correlation Coefficient,
![]() $ {r}_{xy} $
, in Equation 2.11, which we use to determine the information similarity between the soil moisture variables and the proxies.
$ {r}_{xy} $
, in Equation 2.11, which we use to determine the information similarity between the soil moisture variables and the proxies.
 $$ {r}_{x_1{x}_2}=\frac{\sum_i\left({x}_i-\overline{x}\right)\left({y}_i-\overline{y}\right)}{\sqrt{\sum_i{\left({x}_i-\overline{x}\right)}^2{\sum}_i{\left({y}_i-\overline{y}\right)}^2}} $$
$$ {r}_{x_1{x}_2}=\frac{\sum_i\left({x}_i-\overline{x}\right)\left({y}_i-\overline{y}\right)}{\sqrt{\sum_i{\left({x}_i-\overline{x}\right)}^2{\sum}_i{\left({y}_i-\overline{y}\right)}^2}} $$
The second methodology is on the sensitivity of a network to the input variables, for which various methodologies exist. Commonly employed methods for doing so include, but are not limited to: input perturbation analysis, weight analysis, and gradient analysis (Cao et al., Reference Cao, Alkayem, Pan, Novák and Rosa2016; Cao and Qiao, Reference Cao and Qiao2008; Gevrey et al., Reference Gevrey, Dimopoulos and Lek2003; Pizarroso et al., Reference Pizarroso, Portela and Muñoz2022). The method that we employ here is the input perturbation algorithm, where for each input variable,
![]() $ {x}_i $
, we add some increment,
$ {x}_i $
, we add some increment,
![]() $ {\delta}_i $
, that we can vary and then measure the change in output, where
$ {\delta}_i $
, that we can vary and then measure the change in output, where
![]() $ {\delta}_i $
is a proportion of the input value.
$ {\delta}_i $
is a proportion of the input value.
3. Data
The UK Centre for Ecology and Hydrology provides extensive records of hydrometric data from across the UK, with 1602 gauge station records available through the UK National River Flow Archive (NRFA) (UK Centre for Ecology and Hydrology, 2022). For this study, we select representative catchments at difference area scales. Our exemplar catchments are the River Severn at Haw Bridge, selected randomly from the largest 0.5% of catchments with an area of 9895 km2, the Bedford Ouse at Roxton, from the largest 5% of catchments at 1660 km2, and the Findhorn at Shenachie, from the largest 50% of catchments at 416 km2. The elevation, land use, and geology characteristics of these catchments are shown in Figure 2.
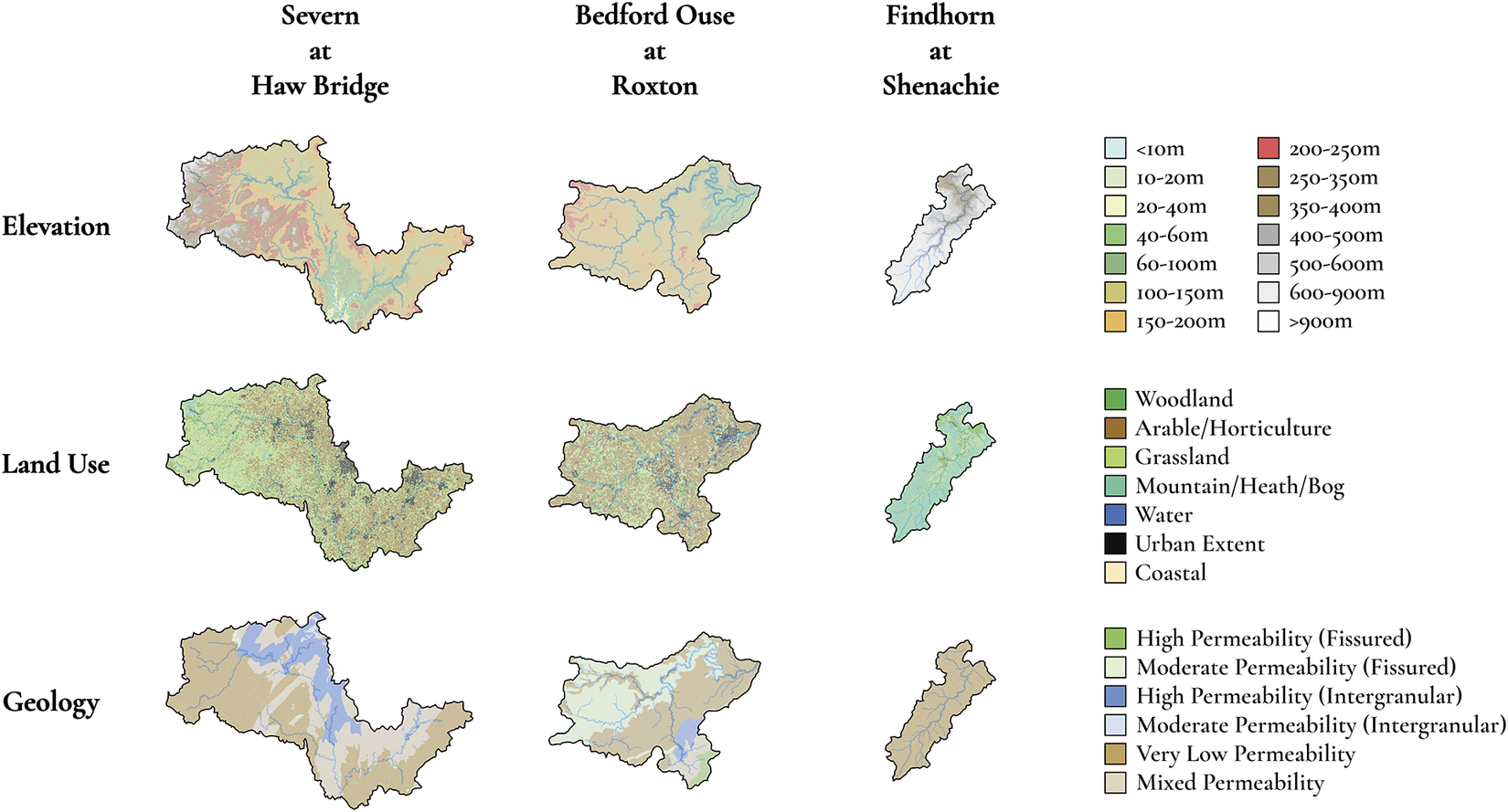
Figure 2. Elevation, land use, and geology maps for the three study catchments; corresponding keys represent the proportion of each catchment that falls under the respective subcategories. Note that the catchments are shown at different scales for visibility. Adapted from the National River Flow Archive (UK Centre for Ecology and Hydrology, 2022).
The three catchments cover highland, lowland, and mixed elevation catchments that also feature a range of different land use scenarios, with the Findhorn at Shenachie being predominantly mountainous, at 74.32% of land cover, and the Bedford Ouse at Roxton featuring a heavy proportion of arable or horticultural farmland and grassland, 51.33% and 29.66%, respectively. The range of geological representation is less pronounced but still significant, with the Findhorn at Shenachie being 100% very low permeability bedrock and the other two catchments having more mixed compositions.
The input meteorological data are extracted from The European Centre for Medium-Range Weather Forecast’s (ECMWF) fifth generation of global climate reanalysis data, ERA5, a modeled data product that utilizes observational data through data assimilation (Hersbach et al., Reference Hersbach, Bell, Berrisford, Biavati, Horányi, Muñoz-Sabater, Nicolas, Peubey, Radu, Rozum, Schepers, Simmons, Soci, Dee and Thépaut2018). This data product is widely used, including in hydrological studies, due to its accuracy and comparability with observations (Hersbach et al., Reference Hersbach, Bell, Berrisford, Hirahara, Horányi, Muñoz-Sabater, Nicolas, Peubey, Radu, Schepers, Simmons, Soci, Abdalla, Abellan, Balsamo, Bechtold, Biavati, Bidlot, Bonavita, Chiara, Dahlgren, Dee, Diamantakis, Dragani, Flemming, Forbes, Fuentes, Geer, Haimberger, Healy, Hogan, Hólm, Janisková, Keeley, Laloyaux, Lopez, Lupu, Radnoti, Rosnay, Rozum, Vamborg, Villaume and Thépaut2020; Nogueira, Reference Nogueira2020; Tarek et al., Reference Tarek, Brissette and Arsenault2020). Soil moisture from ERA5, critical to this study, has also been observed to have a high degree of correlation with observations globally, more so than other data products (Dong et al., Reference Dong, Lai, Wang, Dong, Zhu, Dong and Cen2022; Lal et al., Reference Lal, Singh, Das, Colliander and Entekhabi2022; Li et al., Reference Li, Wu and Ma2020). Although the spatial resolution of ERA5 is relatively coarse, at a grid size of 31 km, its ubiquity is highly compatible with our overarching aim of enabling a globally applicable, physics-informed machine learning approach, one for transfer to regions where rainfall and soil moisture gauges are not routinely, or at all, available (Kidd et al., Reference Kidd, Becker, Huffman, Muller, Joe, Skofronick-Jackson and Kirschbaum2017; Krabbenhoft et al., Reference Krabbenhoft, Allen, Lin, Godsey, Allen, Burrows, DelVecchia, Fritz, Shanafield, Burgin, Zimmer, Datry, Dodds, Jones, Mims, Franklin, Hammond, Zipper, Ward, Costigan, Beck and Olden2022).
The input variables used are precipitation at the surface, four levels of soil moisture, and the variables that affect evapotranspiration: daily average temperature, relative humidity, and the components of wind speed parallel to the earth’s surface, all of which have been taken at a height just above the surface at 1000 hPa. Up to 28 days worth of meteorological data are used per prediction. We also define a set of proxy variables that serve as a replacement for soil moisture inputs. To encapsulate the antecedent conditions in the catchment and to capture seasonal trends we use the 30, 90, and 180 day moving averages for precipitation and temperature.
Catchment boundaries are provided through the NRFA, derived from the Centre for Ecology & Hydrology’s Integrated Hydrological Digital Terrain Model (Morris and Flavin, Reference Morris and Flavin1990, Reference Morris and Flavin1994), with the centroid calculated as we describe in Section 2. Meteorological data are then interpolated at this point using a cubic spline fitting method (Balog et al., Reference Balog, Caputo, Iatauro, Signoretti and Spinelli2023; De Boor, Reference De Boor2001; Tabor and Williams, Reference Tabor and Williams2010).
The streamflow data that form our target output are mean daily gauged data. Though these data are readily available, streamflow response to climatic conditions is smoothed at the daily time step, with the maximum instantaneous peak flow not fully represented (Bartens and Haberlandt, Reference Bartens and Haberlandt2021; Ding et al., Reference Ding, Haberlandt and Dietrich2015; Fill and Steiner, Reference Fill and Steiner2003). This is potentially a greater issue for smaller catchments, where the time for runoff to reach the river is similarly small, causing the instantaneous peak flow to diverge considerably from the mean daily flow (Fill and Steiner, Reference Fill and Steiner2003; Fuller, Reference Fuller1914; Gray, Reference Gray1973). While this issue is apparent, it is not something that we intend to address here and does not diminish the comparison we make in this study.
Finally, the split between training and test data is kept consistent across all three model applications, with the period from 1979 to 2008 used to train model instances, the year 2009 used as a validation set, and the period 2010 to 2019 used to test the model.
4. Results and discussion
4.1. Variable comparison
We first provide analysis of the correlation between the antecedent proxies with the soil moisture variables, in accordance with the methods as described in Section 2, to highlight the information value of these variables and the potential utility of the antecedent proxies. The correlation between soil moisture and the antecedent proxies is shown in Table 1, where
![]() $ {SM}_{Lx} $
is the soil moisture at the level
$ {SM}_{Lx} $
is the soil moisture at the level
![]() $ x $
and
$ x $
and
![]() $ {\mu}_{v:d} $
is the antecedent proxy for a variable
$ {\mu}_{v:d} $
is the antecedent proxy for a variable
![]() $ v $
, either precipitation or temperature, taken over a number of days
$ v $
, either precipitation or temperature, taken over a number of days
![]() $ d $
.
$ d $
.
Table 1. Pearson correlation coefficients between soil moisture-level variables and antecedent proxies, averaged over the three study catchments
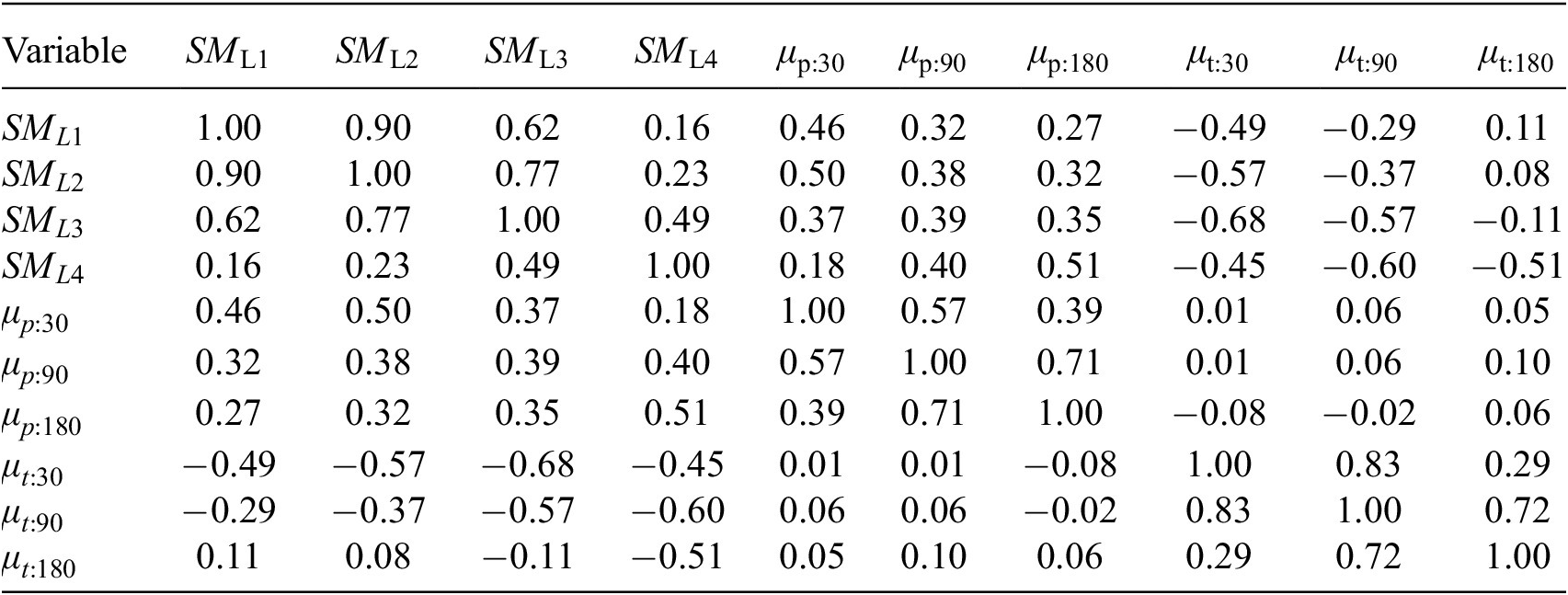
While the soil moisture-level variables exhibit positive correlation among themselves, the correlation between the deepest level, 4, and the shallowest level, 1, is weak. This suggests that there is significant information gain in utilizing all soil moisture levels simultaneously. (This does not mean that the trained neural network will respond to all variables equally: that quantification is shown in the subsequent sensitivity analysis.)
Key to the premise of this work is the strength of correlation between the antecedent proxies and the soil moisture levels. The results are intuitive: shorter-term antecedent proxies have high correlation (positive for precipitation and negative for temperature) with the shallow soil moisture levels; longer-term antecedent proxies exhibit high correlation with the deeper soil moisture levels. It is clear that different information is contained within the antecedent proxies across the timescales. Because we can reason physically that both shallow and deep soil moisture states are important for flow prediction (though the weighting of importance will be catchment dependent) due to their relationship to surface runoff and groundwater recharge, we are justified in selecting antecedent proxy timescales that correlate strongly with both deep and shallow soil moisture states.
4.2. Model results
Our results for the three catchments across all metrics are shown in Table 2, respectively, including results for the models using a meteorological input sequence length of 28 days, 7 days, 7 days with soil moisture, and 7 days with proxy variables. The performance measured by RMSE and MPRE indicates that the highest performing models are those that use the 7-day meteorological input with the inclusion of either the antecedent proxies or soil moisture variables. Increasing the number of days in the meteorological input space continued to increase performance, although we found that the gains in performance started to taper off beyond 28 days and came at the expense of numerical stability during training. From the RB, all models had a tendency to underpredict, though the evidence for which underpredicts the least was inconclusive.
Table 2. MLP model performance in terms of Nash-Sutcliffe efficiency for meteorological input sequence length of 28 days (28), 7 days (7), 7 days with soil moisture (7 + SM), and 7 days with proxy variables (7 + P) (bold typeface indicates highest performance)
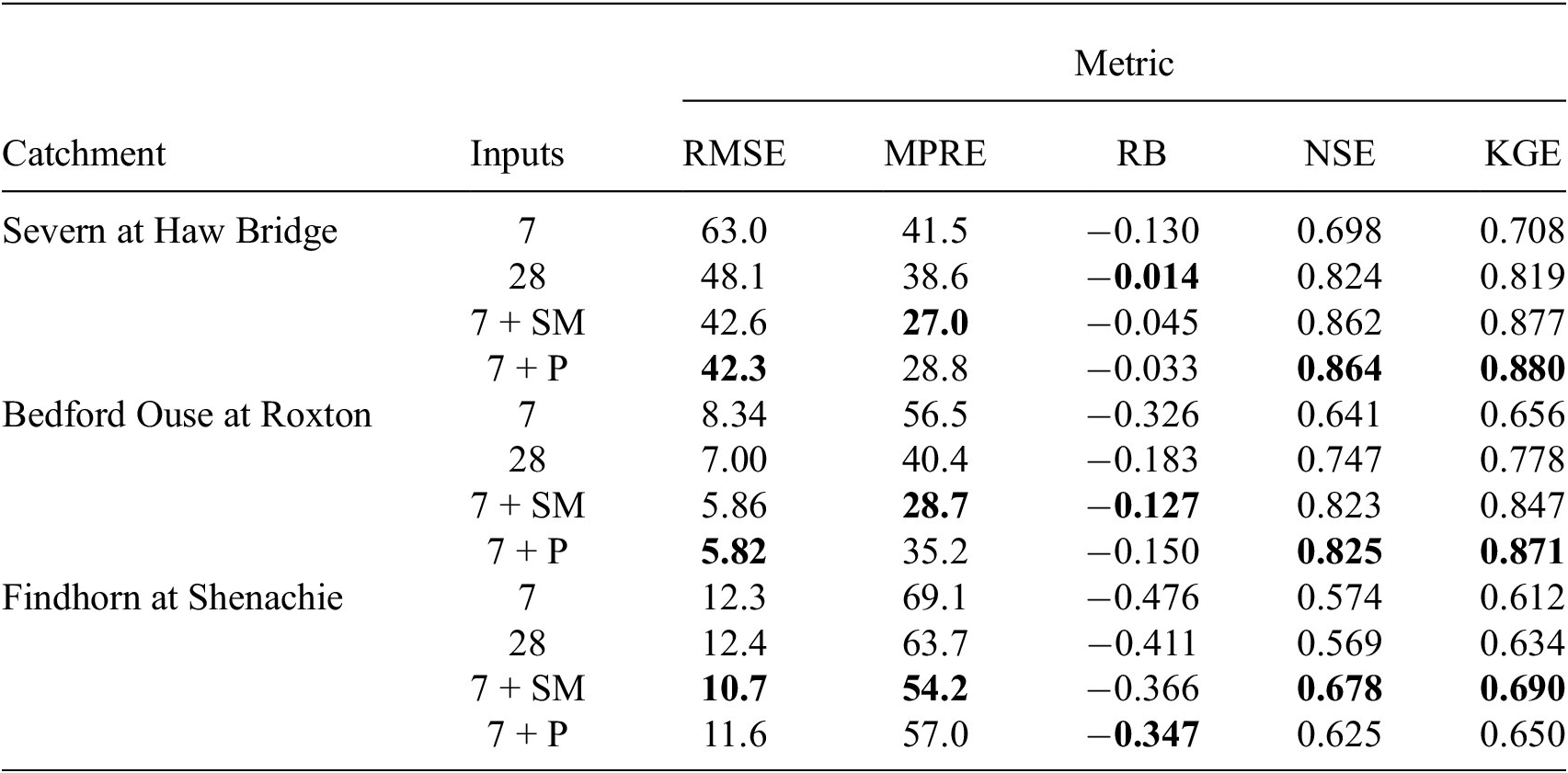
Through examination of the NSE and KGE, however, the overall performance for the Findhorn at Shenachie is clearly lower than that for the other catchments. This was expected due to the smaller size of the catchment potentially leading to a more rapid flow response. Compared to the Bedford Ouse at Roxton, the Findhorn at Shenachie is smaller yet the mean flow rate is higher. The inference is that the response from the catchment requires a finer temporal scale than the daily scale used here. Regardless, we can still see the same pattern emerging that the short variable record in conjunction with either soil moisture or the antecedent proxies results in a model with a high degree of skill. Furthermore, all models exceed our benchmarks and the higher KGE relative to the NSE indicates that the models are predicting peaks and are representing the variability of the flow patterns well.
We present a subset of the results, those for the Severn at Haw Bridge: with the predictions against observations in Figure 3; exemplar streamflow time series observations and predictions for the year 2012 (from the test set) in Figure 4; and the percentage relative error for different percentile bands in Figure 5. The figures for the other catchments are shown in the Supplementary Materials.

Figure 3. Predictions against observations for the Severn at Haw Bridge from the test set of predictions generated using different feature sets as inputs to the MLP model.
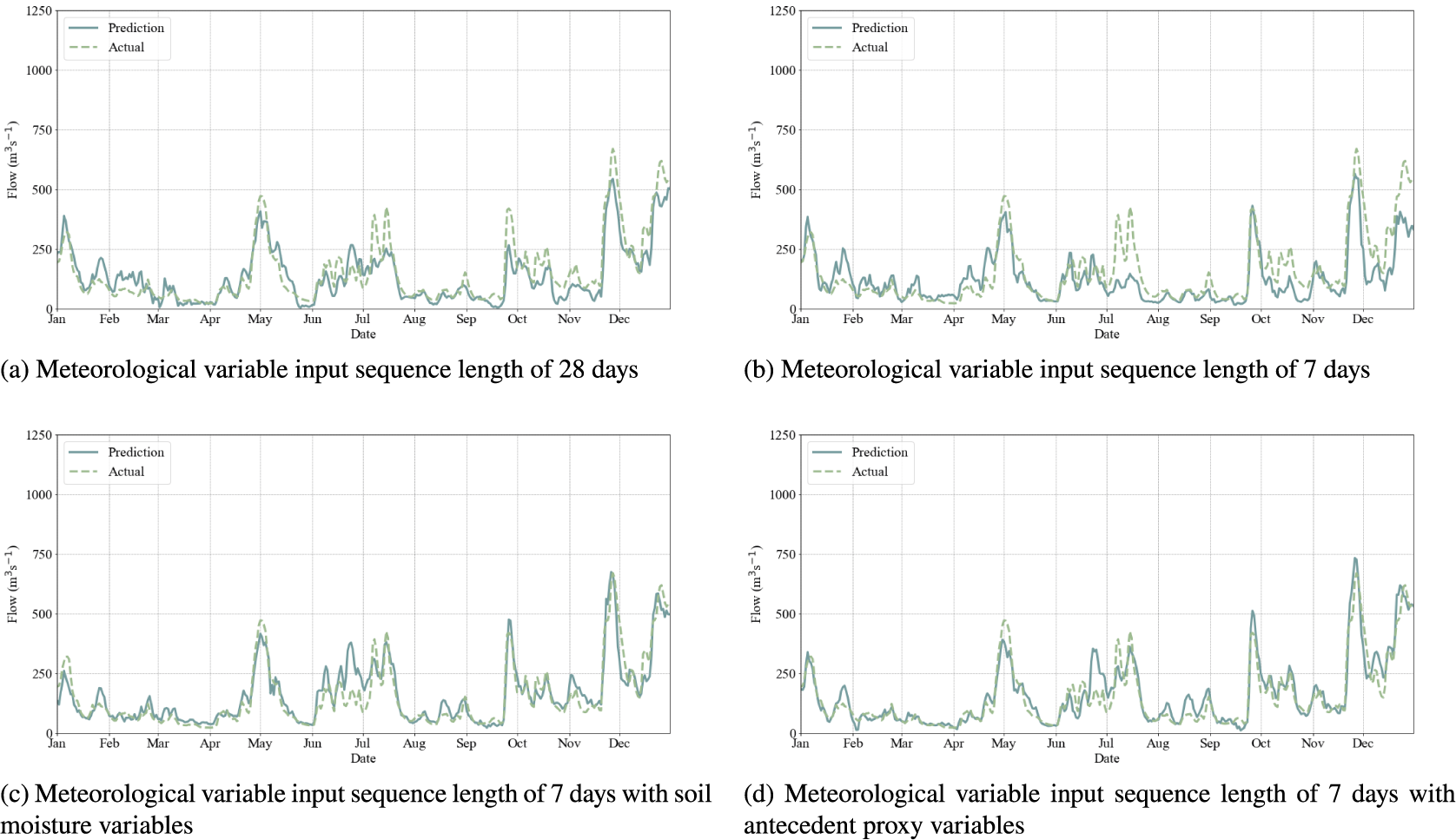
Figure 4. Comparative streamflow time series for the Severn at Haw Bridge in the year, 2012, with both predictions and observations using different feature sets as inputs to the MLP model.
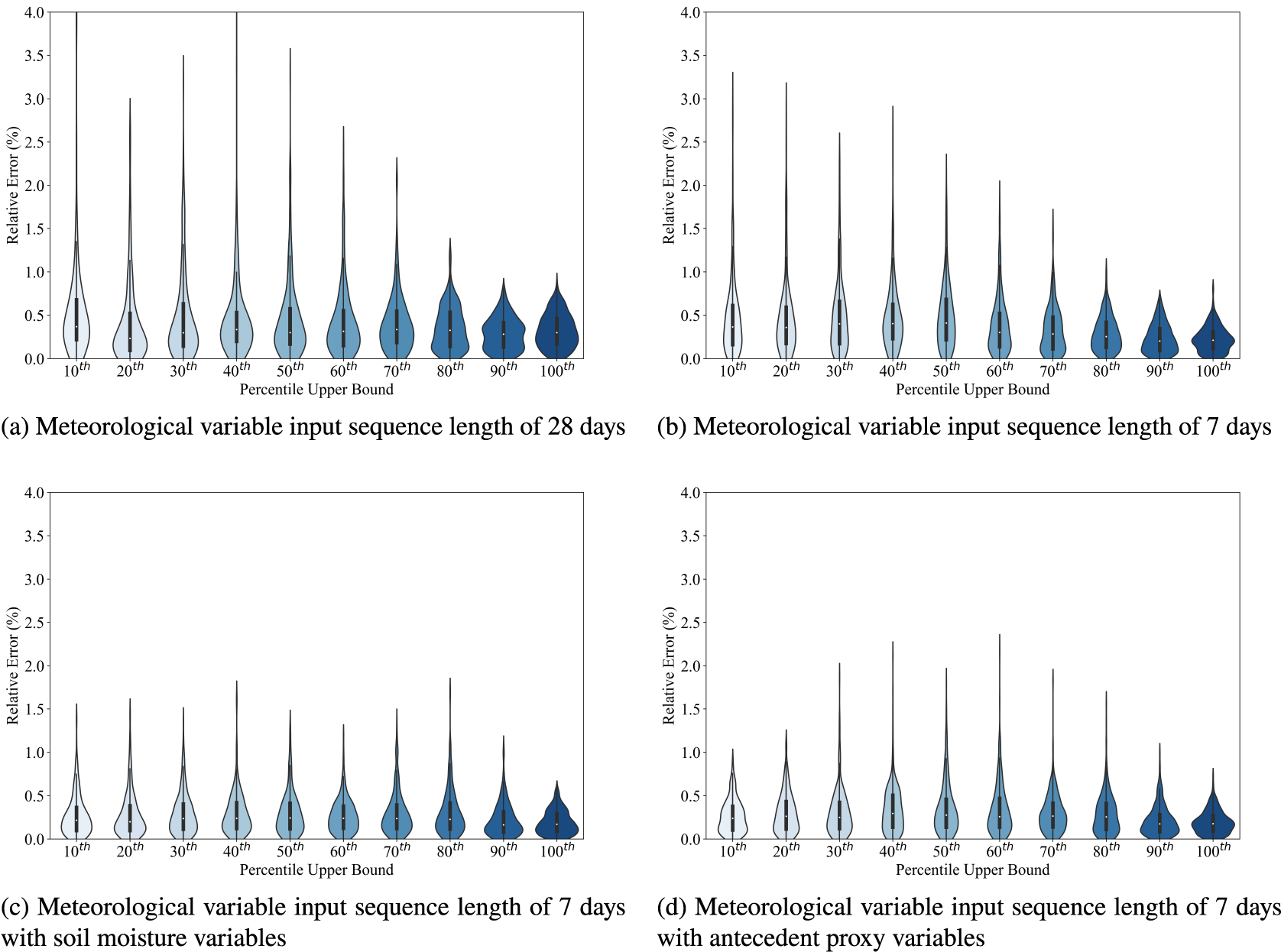
Figure 5. Violin plots of percentage relative error for each of the 10
![]() $ {}^{th} $
percentile bands of flow magnitude (with the upper bound marked on the scale and the lower bound being the preceding upper bound to the left) between observations and predictions for the Severn at Haw Bridge using different feature sets as inputs to the MLP model.
$ {}^{th} $
percentile bands of flow magnitude (with the upper bound marked on the scale and the lower bound being the preceding upper bound to the left) between observations and predictions for the Severn at Haw Bridge using different feature sets as inputs to the MLP model.
Across all three catchments, baseflow and peak flow events are less well captured in the 28-day and 7-day models; whereas this is noticeable for winter peaks in the larger two catchments, all model implementations struggle with the summer peaks for the Findhorn at Shenachie. Using the soil moisture and proxy variable models result in a significant improvement in the representation of baseflow and a more modest improvement in the representation of peak flow events. Model results, while not perfect, are approaching a level of performance that would be considered robust. The set of catchments tested here is, obviously, small and further work may be required to refine the approach further. Having said that, with this framework in place, an alternative departure point from this work might be to move into the multiple catchment setting to prove that this is a suitable climatic framework for constructing a generalizing model; in that context, the catchment descriptors would come into play and, perhaps with more data, enable the learning of small catchment response versus larger catchment response.
4.3. Network sensitivity
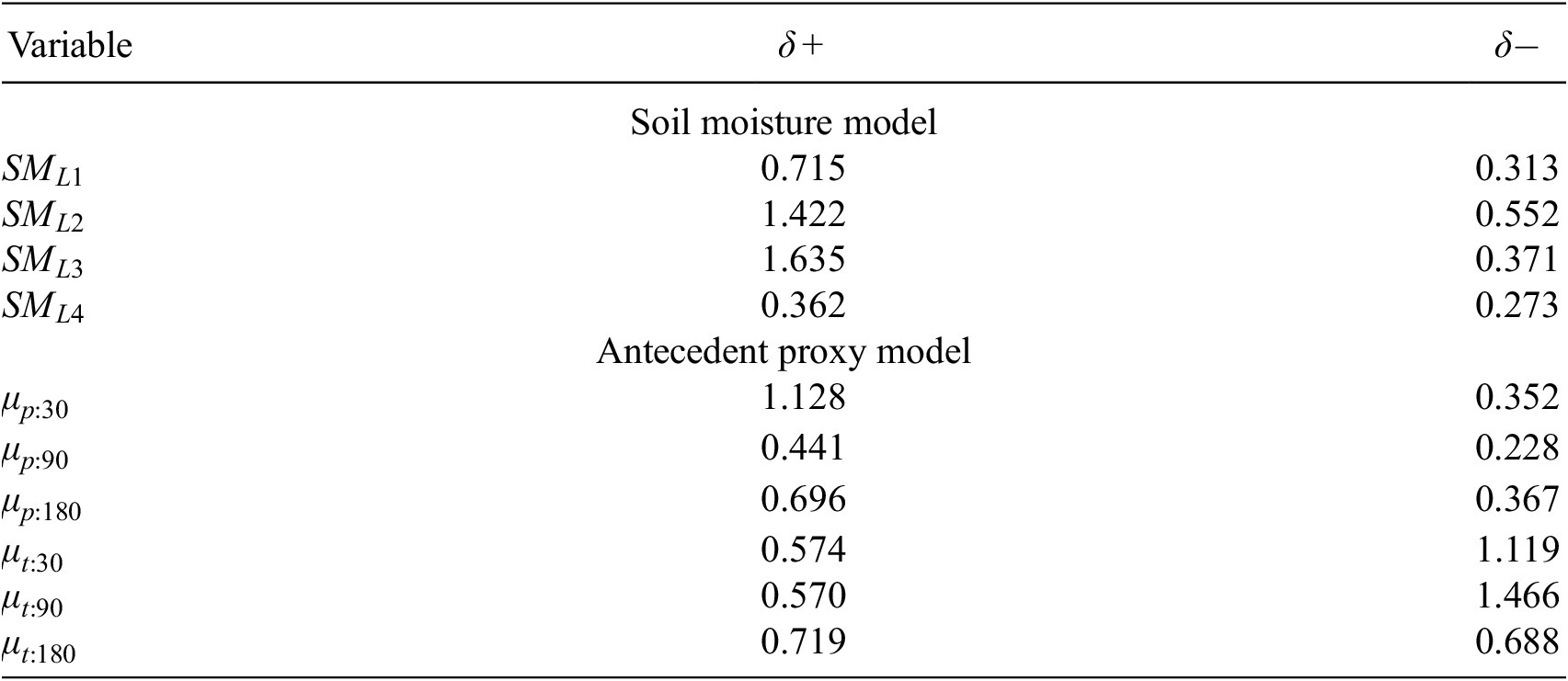
Using the input perturbation algorithm, we assess the sensitivity of the two separate networks trained on either the soil moisture variable set or the antecedent proxy variable set. Sensitivity has been calculated with perturbations in either direction, to account for the varying response to lower temperatures and higher precipitation when compared with lower precipitation and higher temperatures; arguably, utilization of the gradient method of sensitivity analysis might avoid this issue and will be explored in further work. A subset of results averaged across the three study catchments is presented in Table 3. Model sensitivity to the soil moisture variables and the antecedent proxy variables is of a similar order of magnitude; if we consider the aggregate sensitivity to these variable sets, then it is roughly equivalent over these two variable sets for the positive perturbation but higher for the antecedent variable set for the negative perturbation. Essentially, the response of the network to these variables appears to be similar. In terms of whether or not all the proxies or soil moisture levels are required to force the model, due to the varying information represented and the relative sensitivities, then it would be hard to argue that any one variable was not required in either the soil moisture to antecedent proxy variable sets, though soil moisture Level 1 might perhaps be well represented by and surplus to soil moisture Level 2 and short-term precipitation.
Table 3. Average model sensitivity to individual soil moisture and antecedent proxy inputs using positive and negative perturbations for the two different model setups
When examining the response due to the daily meteorological variables, it is worth noting that the Findhorn at Shenachie, as a smaller, less permeable and therefore flashier catchment, is far more sensitive to the most recent 24 hours worth of rainfall when compared to the larger catchment that feeds the Severn at Haw Bridge. Overall, the closer to the flow event, the more impactful the perturbation. The network sensitivity drops off substantially after 5 days (backward from the event), as shown in Figure 6, and sensitivity to daily meteorological forcing is superseded by sensitivity to the soil moisture levels or antecedent proxies after this point. Thus, the antecedent proxies are capable of replacing longer meteorological records and the soil moisture levels, likely encapsulating much of the information encoded within the aforementioned variables.
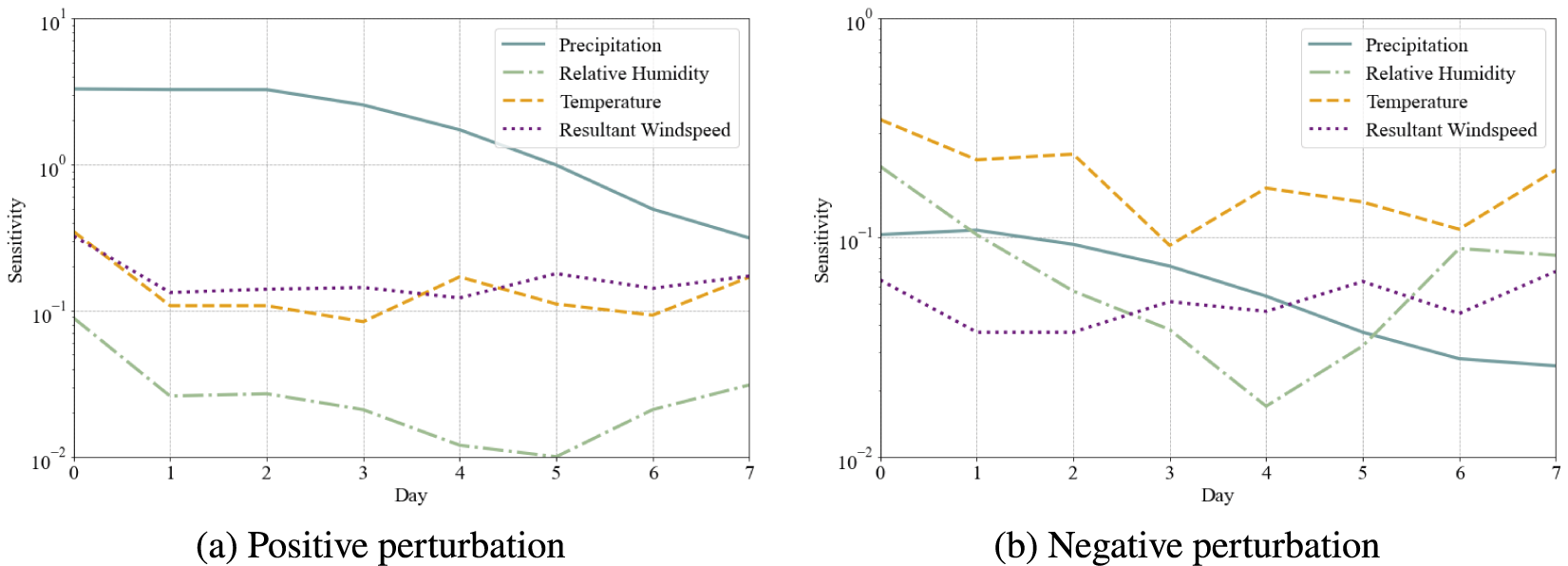
Figure 6. Average network sensitivity to daily meteorological variables under a positive perturbation (left) and negative perturbation (right), with logarithmic scales on the y axis.
4.4. Study limitations
We note two areas in particular that were beyond the scope of this paper but are worth future exploration. The first being that, although we have quantified the error across percentile ranges, we have not developed the model to allow for prediction and reconstruction of the flow volume into base and peak flows. Though the output data we used were average daily flow, empirical methods exist for the reconstruction of base and peak flows that can be parameterized or trained on a per catchment basis (Fathzadeh et al., Reference Fathzadeh, Jaydari and Taghizadeh-Mehrjardi2017; Jimeno-Sáez et al., Reference Jimeno-Sáez, Senent-Aparicio, Pérez-Sánchez, Pulido-Velazquez and Cecilia2017). The second area is on the quantification of uncertainty, in terms of both the aleatoric and epistemic uncertainty. Inadequate quantification of uncertainty can hinder the utilization of artificial intelligence approaches in decision and policy-making processes (Borrego et al., Reference Borrego, Monteiro, Ferreira, Miranda, Costa, Carvalho and Lopes2008; Cabaneros and Hughes, Reference Cabaneros and Hughes2022) and provision of model uncertainty therefore aids adoption.
5. Conclusion
Through our approach, we have minimized the internal measured data burden by replacing relatively inaccessible variables with more accessible proxies. Subsequent model development can focus on more readily obtainable data in addition to offering a reduction in input space dimensionality that reduces the total number of model parameters. Our belief is that model parsimony helps improve model interpretability and could increase adoption of machine learning methods in operational hydrology. Leveraging domain knowledge, in this case through physically reasoned variable selection, can deliver high performance in conjunction with, rather than at the expense of, model parsimony.
While more modern neural network architectures may offer performance improvements and even uncertainty predictions (for example, Gaussian or Neural Processes (Garnelo et al., Reference Garnelo, Rosenbaum, Maddison, Ramalho, Saxton, Shanahan, Teh, Rezende, Eslami, Dy and Krause2018; Rasmussen, Reference Rasmussen, Bousquet, von Luxburg and Rätsch2004)), it was not our intention here to obtain best in class performance. Instead, we have highlighted how it is possible to limit the number of variable records required as input; and use a shortened temporal subset of forcing variables alongside climatological proxies to represent the longer-term hidden state of a catchment (here, the water storage as soil moisture). This in turn enables a more generic, yet still expressive, input space with which to force hydrological models that is easily generalized to other catchments.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/eds.2024.48.
Author contribution
Conceptualization: R.E.R., A.M.; Data curation: R.E.R.; Funding acquisition: R.E.R., S.H., A.M., E.S.; Methodology: R.E.R., A.M., D.K.; Project administration: R.E.R., S.H., A.M., E.S.; Software: R.E.R., S.H.; Supervision: S.H., A.M., E.S.; Visualization: R.E.R., A.M.; Writing—Original draft: R.E.R., D.K.; Writing—Review and editing: R.E.R., D.K.
Competing interest
The authors declare no competing interests exist.
Data availability statement
The data required to reproduce these results are available at the NRFA (Dixon et al., Reference Dixon, Hannaford and Fry2013) using the data portal https://nrfa.ceh.ac.uk/data/search or API https://nrfaapps.ceh.ac.uk/nrfa/nrfa-api.html and from the Copernicus Climate Data Store https://doi.org/10.24381/cds.143582cf. We have made the code to run the model available at https://doi.org/10.5281/zenodo.13861688.
Ethics statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by a grant from the Engineering and Physical Sciences Research Council (EP/R512461/1). This research was supported by a Fellowship from the Royal Commission for the Exhibition of 1851.
Supplementary material
The supplementary material for this article can be found at http://doi.org/10.1017/eds.2024.48.














Comments
Dear Professor Monteleoni,
We wish to submit an original research article, entitled Streamflow Prediction Using Artificial Neural Networks & Soil Moisture Proxies, for consideration by Environmental Data Science. We confirm that this work is original and has not been published elsewhere, nor is it currently under consideration for publication elsewhere.
In this paper, we demonstrate how internal variables of hydrological systems can be represented within the feature set of a machine learning model, resulting in a modelling approach more easily applied to different geographies where data availability might not support complex modelling approaches whilst also enabling practitioners to hold a higher level of confidence in machine learning models.
Given the potential impacts of climate change, both in terms of flooding and water resources, being able to rapidly develop modelling approaches with greater global applicability and, subsequently, to generate projections of said impacts under different scenarios is of high importance and likely to be of interest to hydrologists and decision makers around the world. This paper helps to provide a parsimonious modelling foundation that we might hope to build upon to generalise between catchments and generate hydrological predictions in the absence of data.
We have no conflicts of interest to disclose. Please address all correspondence concerning this manuscript to me at rer44@cam. ac.uk.
Thank you for your consideration of this manuscript.
Yours Sincerely,
Robert Edwin Rouse,
Doran Khamis,
Scott Hosking,
Allan McRobie,
Emily Shuckburgh