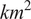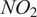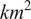Impact Statement
Data fusion is commonly employed with the assumption of having access to a substantial volume of data. Unfortunately, measurement campaigns of complex phenomena in isolated areas often result in significantly reduced amount of information. We show that combining geostatistical tools and deep learning models into a distance attention overcomes this issue. We applied our method to static environmental phenomena using synthetic sensor devices of different measurement characteristics representative of real sensors. The encouraging results suggest that such methods can be applied to space-time environmental phenomena.
1. Introduction
Monitoring real-time environmental phenomena enables experts to detect unusual events such as abnormal air quality, greenhouse gas emission sources, and extreme meteorological events, among others. For this purpose, numerical modeling tools are developed and networks of monitoring stations as well as satellite-based remote sensing provide data. Nonetheless, providing highly accurate information at high spatial and temporal resolution on vast areas requires heavy numerical processing, high-technology sensors, and an expensive maintenance that only national organizations and large companies can afford. To reduce these costs, high quality sensor devices are deployed more sporadically, and, given suitable data quality, low-cost sensors (Castell et al., Reference Castell, Dauge, Schneider, Vogt, Lerner, Fishbain, Broday and Bartonova2017; Hassani et al., Reference Hassani, Bykuć, Schneider, Zawadzki, Chaja and Castell2023; Schneider et al., Reference Schneider, Vogt, Haugen, Hassani, Castell, Dauge and Bartonova2023; Van Poppel et al., Reference Van Poppel, Schneider, Peters, Yatkin, Gerboles, Matheeussen, Bartonova, Davila, Signorini, Vogt, Dauge, Skaar and Haugen2023) can complement these. In addition, numerical models are run from global to local scale with highly variable spatial resolution. Finally, a combination of these sources is processed to retrieve the target information, for instance, low-cost sensor calibration (De Vito et al., Reference De Vito, Esposito, Salvato, Popoola, Formisano, Jones and Di Francia2018, Reference De Vito, Esposito, Castell, Schneider and Bartonova2020; Ionascu et al., Reference Ionascu, Castell, Boncalo, Schneider, Darie and Marcu2021) and land-use regression (Hong et al., Reference Hong, Pinheiro, Minet, Hatzopoulou and Weichenthal2019; Weichenthal et al., Reference Weichenthal, Dons, Hong, Pinheiro and Meysman2021) for air quality, atmospheric temperature downscaling (Chau et al., Reference Chau, Bouabid and Sejdinovic2021), downscaling of satellite data for air quality (Stebel et al., Reference Stebel, Stachlewska, Nemuc, Horálek, Schneider, Ajtai and Zehner2021), and multi-sensor data fusion to estimate evapotranspiration (Semmens et al., Reference Semmens, Anderson, Kustas, Gao, Alfieri, McKee, Prueger, Hain, Cammalleri, Yang and Xia2016).
In environmental science, data fusion based on neural networks and machine learning is used to combine regularly spaced gridded datasets, such as satellite data (Schneider et al., Reference Schneider, Hamer, Kylling, Shetty and Stebel2021, Shetty et al., Reference Shetty, Schneider, Stebel, Hamer, Kylling and Berntsen2024) and images from unmanned aerial vehicles, thereby enabling resolution space-time enhancement, pansharpening, and classification (Ghamisi et al., Reference Ghamisi, Rasti, Yokoya, Wang, Hofle, Bruzzone, Bovolo, Chi, Anders, Gloaguen and Atkinson2019). For datasets with dense and irregular point cloud data, such as hyperspectral imaging and lidar, point fusion (Xu et al., Reference Xu, Anguelov and Jain2018) enables classification, clustering, and point enrichment.
In the case of sparse point clouds, data fusion is often based on geostatistical techniques such as kriging (Wackernagel, Reference Wackernagel2003; Rue et al., Reference Rue, Riebler, Sørbye, Illian, Simpson and Lindgren2017) (both with and without spatial auxiliary variables), for example, for spatiotemporal mapping of air quality (Schneider et al., Reference Schneider, Castell, Vogt, Dauge, Lahoz and Bartonova2017, Reference Schneider, Castell, Dauge, Vogt, Lahoz, Bartonova, Bordogna and Carrara2018). In addition, data assimilation approaches, such as Kalman filter, Optimal Interpolation, 3D-Var, and 4D-Var (Miyoshi et al., Reference Miyoshi, Sato and Kadowaki2010; Wattrelot et al., Reference Wattrelot, Caumont and Mahfouf2014; Lussana et al., Reference Lussana, Tveito, Dobler and Tunheim2019; Mijling, Reference Mijling2020; Hassani et al., Reference Hassani, Schneider, Vogt and Castell2023; Schneider et al., Reference Schneider, Vogt, Haugen, Hassani, Castell, Dauge and Bartonova2023), in which deep learning has been recently integrated (Arcucci et al., Reference Arcucci, Zhu, Hu and Guo2021; Peyron et al., Reference Peyron, Fillion, Gürol, Marchais, Gratton, Boudier and Goret2021), use the uncertainty of each data source to determine their weight while fusing. While kriging requires solving the kriging equation system, other less computational processing demanding kernel regression approaches enable the prediction of space-time phenomena such as a graph convolution network (Appleby et al., Reference Appleby, Liu and Liu2020) and a GRNN (Specht, Reference Specht1991; Robert et al., Reference Robert, Foresti and Kanevski2013).
This research work is carried out in the context of advancements in measurement campaigns, where heterogeneous, mobile, and autonomous devices (Jońca et al., Reference Jońca, Pawnuk, Bezyk, Arsen and Sówka2022; Samad et al., Reference Samad, Alvarez Florez, Chourdakis and Vogt2022; Scheller et al., Reference Scheller, Mastepanov and Christensen2022) monitor local phenomena in isolated areas (Miner et al., Reference Miner, Turetsky, Malina, Bartsch, Tamminen, McGuire, Fix, Sweeney, Elder and Miller2022) for prediction purposes, for instance, spatial mapping (Hassani et al., Reference Hassani, Castell, Watne and Schneider2023). We limit our paper to sensors being preprocessed at level 1, following (Schneider et al., Reference Schneider, Bartonova, Castell, Dauge, Gerboles, Hagler, Huglin, Jones, Khan, Lewis, Mijling, Müller, Penza, Spinelle, Stacey, Vogt, Wesseling and Williams2019). We have thus observation devices providing sparse measurements at different spatial and temporal resolutions, with different measurement qualities, and possibly at non-regular sampling frequencies. In this context, data fusion of environmental sensor devices faces two challenges: i) fusing nonoverlapping multiple sources of information with heterogeneous characteristics and ii) predicting complex phenomena with sparse data. To overcome these challenges, we propose a methodology based on three axes: i) the use of a priori information about measurement characteristics and its quality to weight their influence in data fusion, ii) an inclusion of deep neural networks into ordinary kriging (OK) and GRNN, and iii) determining an attention framework as Vaswani et al. (Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017) to enable inter-comparison between the prediction approaches.
Our paper is structured as follows. Section 2 describes the materials and methods used in this study. Section 2.1 describes the measurement characteristics in a network of sparse, heterogeneous, and mobile sensors devices. Section 2.2 describes the adaptive distance attention, Section 2.3 describes the GRNN and OK as adaptive distance attention, Section 2.4 describes the data fusion model architecture, Section 2.5 describes the three cases studies of this study, and Section 2.6 describes the experimentation plan. Section 3 presents the results and the discussion. Section 3.1 presents the metrics for the different data fusion models applied to the three case studies, Section 3.2 presents the effect of the data fusion model and the measurement campaign on the learnable parameters, and Section 3.3 presents a discussion of the results. Finally, the conclusion is presented in Section 4.
2. Materials and methods
2.1. Measurement characteristics in a network of sparse, heterogeneous, and mobile sensors devices
In this section, we describe the characteristics that are common to measurements from several heterogeneous sensor devices.
Let us assume a network of several sensor devices measuring the same physical phenomena. We assume all sensor devices to be at level 1 according to Schneider et al. (Reference Schneider, Bartonova, Castell, Dauge, Gerboles, Hagler, Huglin, Jones, Khan, Lewis, Mijling, Müller, Penza, Spinelle, Stacey, Vogt, Wesseling and Williams2019) and provide measurements with an identical unit. In this article, we use the term sensor device to describe any instrumentation that provides observations in space and time.
The measurements of these sensor devices are described by five characteristics: their spatial and temporal resolution, their location, their sampling frequency, and their quality. These characteristics are intrinsic to the device, for example, the quality of the sensor, the electronic hardware, the mechanical structure, the programmatic procedures, and the telecommunication method, to name a few. In our study, we assume sensor devices to be mobile, and being able to provide, for each sampling, a constant measurement over an area surrounding their location. The characteristics of the measurements used in this study are schematically presented in Figure 1.
Figure 1. Sequence of two timesteps of a network of heterogeneous sensors measuring spatial phenomena. A crossed circle represents a sensor device whose measurement is representative at this point. A square represents a sensor whose measure represents an average of the phenomena surrounding this area. The quality of the measurement goes from high (color green), to medium (color orange) and to low (color red). Sensor device might be mobile and not providing measurement at every timestep.
2.1.1. Measurement resolution
Without losing generality, we focus here on the spatial resolution of measurement characterized by a shape in Figure 1. A crossed circle represents a sensor device whose measure is representative at this point, and a square represents a sensor whose measure represents an average of the phenomena surrounding this area. The larger the size of the shape the larger the domain of the average and the lower is the spatial resolution. We assume each type of sensor device having an area representative of their measurement to be of any shape. Instead of using measurement resolution as key, and to increase the amount of information, we assume any points located under this shape to be constant. Each value within the shape is then characterized by the same measurement quality.
2.1.2. Measurement quality
As illustrated in Figure 1, the quality of the measurement ranges from high (color green), to medium (color orange), and finally to low (color red). For example, sensor devices designed as green crossed circle can be seen as reference monitoring stations and red crossed circle as low-cost sensor devices. Accuracy and precision are used in this study to quantify the quality of the measurements, and are schematically explained in Figure 2. A comparison of several sensor devices is possible by incorporating their specific accuracy and precision as depicted in Figure 3. The higher the accuracy and the precision, the closer is the measure to ground truth. Both accuracy and precision are considered as metrics processed over time. Because the ground truth is unknown, these metrics are determined with the measurements of the sensor device against the ones of a reference device whose measurements are of high quality. We assume that several items of a specific sensor device provided by one manufacturer get identical accuracy and precision. Realistically, we assume each type of sensor device to be tested beforehand either in laboratory conditions or by co-location with a reference sensor device (Castell et al., Reference Castell, Dauge, Schneider, Vogt, Lerner, Fishbain, Broday and Bartonova2017; Schneider et al., Reference Schneider, Castell, Dauge, Vogt, Lahoz, Bartonova, Bordogna and Carrara2018; Vogt et al., Reference Vogt, Schneider, Castell and Hamer2021). Accuracy and precision are thus a priori information about a sensor device.
Figure 2. Schematic description of accuracy and precision for three identical sensor devices measuring one phenomenon. The center of each target represents the phenomena to be measured. Case (a) sensor devices with high accuracy and high precision, cases (b) and (c) sensor devices with low accuracy and high precision, and case (d) sensor devices with high accuracy and low precision.
Figure 3. Accuracy-precision diagram representing the measurement quality of three types of sensor devices: a reference station, a medium-cost sensor device, and a low-cost sensor device.
In our study, we use root mean square error (RMSE) as accuracy and variance as precision. Large values of RMSE imply low accuracy and small values of RMSE implies high accuracy. In addition, large values of variance imply low precision, and small values of variance imply high precision. The expression of RMSE reads:
$$ RMSE\left(\hat{V},V\right)=\sqrt{\frac{1}{N}\sum \limits_i^N{\left({\hat{V}}_i-{V}_i\right)}^2} $$
with
$ {\hat{V}}_i $
the measurement of the sensor device at time
$ i $
and
$ {V}_i $
, the measurement of the reference sensor device, and
$ N $
the amount of timesteps.
And the expression of variance reads:
$$ variance\left(\hat{V},V\right)=\frac{1}{N}\sum \limits_i^N{\left(|{\hat{V}}_i-{V}_i- bias|\right)}^2 $$
where
$ bias $
being determined as
$ \frac{1}{N}{\sum}_i^N\left({\hat{V}}_i-{V}_i\right) $
.
2.1.3. Measurement sampling and device mobility
As presented in Figure 1, any sensor device has a specific geographical location. Some sensor devices might have issues in providing a measurement at regular frequency; for instance, one red square and one orange crossed circle did not provide any measurement at timestep 2. Besides, some sensor devices might be mobile; for instance, two squares and two crossed circles moved from their original locations between timestep 1 and timestep 2. Each measurement is thus related to a location and a timestamp, used as keys. No measurement does not provide any information and will not be replaced by any fill-in methods.
2.2. Adaptive distance attention
This section aims at presenting adaptive distance attention as a framework for prediction that satisfies the measurement characteristics of a network of sparse and heterogeneous sensor devices.
Let us assume a network of
$ k $
reference stations located in
$ {x}_i $
with measurements
$ {V}_i $
following a Normal distribution. We assume the mean and the standard deviation of the Normal distribution to be stationary. A general formulation of a spatial prediction that suits both OK (Wackernagel, Reference Wackernagel2003), and GRNN (Specht, Reference Specht1991) is presented as follows: the prediction
$ {\hat{V}}_{\ast } $
at location
$ {x}_{\ast } $
is estimated from a) an ensemble of weights involving the Euclidean distance between the location of the target and the locations of the predictors
$ \parallel {x}_{\ast },{x}_i\parallel $
, that is, the distance of de-correlation of the phenomenon
$ R $
and b) the value of the predictors
$ {V}_i $
. Figure 4 illustrates this general formulation. The closer a station is to the prediction location, the higher is its weight and thus the involvement of its value. For example, the prediction at location
$ {x}_{\ast } $
will be characterized mostly by the value of the station located at
$ {x}_2 $
. The value located at
$ {x}_1 $
will get a lower impact. Besides, values from stations located at
$ {x}_3 $
,
$ {x}_4 $
, and
$ {x}_5 $
will get a minor weight due to their locations outside of the area of representativity delimited by the circle of radius R. Following this description, we write the prediction
$ {\hat{V}}_{\ast } $
at location
$ {x}_{\ast } $
as:
$$ {\hat{V}}_{\ast }=\sum \limits_{i=1}^kA\left(\frac{\parallel {x}_{\ast },{x}_i\parallel }{R}\right){V}_i $$
Figure 4. Schematic illustration of a network where each station is identified as
$ \left\{{x}_i,{V}_j\right\} $
, the location of the prediction is identified as
$ {x}_{\ast } $
, and its area of similitude is characterized by a radius
$ R $
.
where
$ A $
represents the attention weight based on a score involving the Euclidean distance between
$ {x}_i $
and
$ {x}_{\ast } $
.
We replace the expression
$ 1/R $
by
$ W $
to avoid any issues of division by zero while training a model in Section 2.6. We call
$ W $
the learnable parameter. Finally, following the notation related to attention in Vaswani et al. (Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017), we call
$ {x}_{\ast } $
the query
$ Q $
and
$ {x}_i $
the key
$ K $
. Then, expression 2.3 writes:
$$ {\hat{V}}_Q=\sum \limits_{i=1}^kA\left(\parallel Q,K\parallel W\right){V}_i $$
2.2.1. Multi-dimension
As done in Kyriakidis and Journel (Reference Kyriakidis and Journel1999) and (Li et al. (Reference Li, Wang and Yuan2020), the query
$ Q $
and the key
$ K $
can represent both space and time. More generally, we let
$ Q $
and
$ K $
represent a
$ d $
-dimensional space. Besides,
$ Q $
and
$ K $
can both represent multiple locations. Thus, we have
$ Q $
a matrix
$ \in {\mathrm{\mathbb{R}}}^{q\times d} $
, and
$ K $
a matrix
$ \in {\mathrm{\mathbb{R}}}^{k\times d} $
.
2.2.2. Adaptive parameter
In the d-dimension, processing the attention weight function faces an anisotropy effect. Thus, it requires the learnable parameter
$ W $
to be adaptive (Robert et al., Reference Robert, Foresti and Kanevski2013) to each dimension of
$ Q $
and
$ K $
. More generally, we let the parameter be adaptive for any points of
$ K $
and
$ Q $
. Consequently, we have two learnable parameters depending, respectively, of
$ Q $
and
$ K $
, written, respectively,
$ {W}_Q\in {\mathrm{\mathbb{R}}}^{q\times d} $
and
$ {W}_K\in {\mathrm{\mathbb{R}}}^{k\times d} $
.
2.2.3. Multivariable
We let
$ V $
and
$ \hat{V} $
describe more than one variable
$ v $
. Nonetheless, we keep the number of variables identical for both the value
$ V $
and the prediction
$ \hat{V} $
. Thus, we see
$ V $
being a matrix
$ \in {\mathrm{\mathbb{R}}}^{k\times v} $
and
$ \hat{V} $
a matrix
$ \in {\mathrm{\mathbb{R}}}^{q\times v} $
.
Our multivariable prediction with a multidimensional adaptive attention then reads:
$$ {\hat{\boldsymbol{V}}}_{\boldsymbol{Q}}=\sum \limits_{i=1}^kA\left(\parallel {\boldsymbol{W}}_{\boldsymbol{Q}}\boldsymbol{Q},{\boldsymbol{W}}_{\boldsymbol{K}}{\boldsymbol{K}}_i\parallel \right){\boldsymbol{V}}_i $$
2.3. GRNN and OK as adaptive distance attention
This section is dedicated to the integration of two prediction methods, namely GRNN and OK, within the context of an adaptive distance attention framework.
GRNNs follow the Nadaraya–Watson kernel regression (Nadaraya, Reference Nadaraya1964; Watson, Reference Watson1964):
$$ {\hat{\boldsymbol{V}}}_{\boldsymbol{Q}}=\sum \limits_{i=1}^k\frac{K_R\left(\boldsymbol{Q},\boldsymbol{K}\right)}{\sum_{j=1}^k{K}_R\left(\boldsymbol{Q},\boldsymbol{K}\right)}{\boldsymbol{V}}_i $$
where
$ {K}_R $
represents a kernel with bandwidth
$ R $
.
GRNN is based on an isotropic radial basis function
$ {e}^{-\parallel \boldsymbol{Q},\boldsymbol{K}{\parallel}^22{R}^2} $
as parametric kernel. Finally, by using the softmax expression
$ {e}^{u_i}/{\sum}_{j=1}^k{e}^{u_j} $
, expression 2.5 becomes:
$$ {\hat{\boldsymbol{V}}}_{\boldsymbol{Q}}=\sum \limits_{i=1}^k{A}_{S,G}\left(\parallel {\boldsymbol{W}}_{\boldsymbol{Q}}\boldsymbol{Q},{\boldsymbol{W}}_{\boldsymbol{K}}\boldsymbol{K}\parallel \right){V}_i $$
with subscript
$ S $
as softmax function and superscript
$ G $
as Gaussian kernel.
OK gets its attention weights by solving the kriging system
$ {\lambda}_{\boldsymbol{Q}}={\varLambda}^{-1}{\varLambda}_{\boldsymbol{Q}} $
, where
$ \varLambda $
represents the semi-variogram matrix. In the case of
$ Q $
representing a single location, we obtain:
$$ {\lambda}_Q=\left(\begin{array}{c}{\lambda}_1\\ {}\vdots \\ {}{\lambda}_k\\ {}\mu \end{array}\right),\varLambda =\left(\begin{array}{cccc}{\Lambda}_{1,1}& \cdots & {\Lambda}_{1,k}& 1\\ {}\vdots & \ddots & \vdots & \vdots \\ {}{\Lambda}_{k,1}& \cdots & {\Lambda}_{k,k}& 1\\ {}1& \cdots & 1& 0\end{array}\right),{\varLambda}_Q=\left(\begin{array}{c}{\Lambda}_{1,Q}\\ {}\vdots \\ {}{\Lambda}_{k,Q}\\ {}1\end{array}\right) $$
where
$ \mu $
is a Lagrangian multiplier and
$ {\Lambda}_{i,j} $
represents the semi-variogram between location
$ {x}_i $
and
$ {x}_j $
Assuming an existing function linalg that solves the linear kriging system and using the case where the variogram follows an exponential function
$ 1-{e}^{-\parallel {x}_{\ast },{x}_i\parallel W} $
of variance 1 and range
$ 1/W $
, expression 2.5 becomes:
$$ {\hat{\boldsymbol{V}}}_{\boldsymbol{Q}}=\sum \limits_{i=1}^k{A}_{L,E}\left(\parallel {\boldsymbol{W}}_{\boldsymbol{Q}}\boldsymbol{Q},{\boldsymbol{W}}_{\boldsymbol{K}}\boldsymbol{K}\parallel \right){\boldsymbol{V}}_i $$
with subscript
$ L $
as linalg function and superscript
$ E $
as an exponential kernel.
Although alternative kernel types and semi-variograms are applicable to GRNN and OK, our emphasis lies on the utilization of simpler variants. Specifically, we prioritize those that a) allow learnable parameters to impart richness to the structure and b) mitigate the risk of encountering issues related to infinite loss during model training.
2.4. Data fusion model architecture
This section is dedicated to introducing our data fusion approach for predicting values, along with a detailed exploration of its underlying model architecture.
Our data fusion uses a similar approach as cross-kriging (Journel and Huijbregts, Reference Journel and Huijbregts1978) in the distance attention framework. An attention weight is processed using queries
$ Q $
and keys
$ K $
belonging to two different networks. During the training phase, a first network, called
$ X $
, provides
$ Q $
and their respective values as targets, and network
$ Y $
provides
$ K $
and values
$ V $
. During the prediction phase, the network
$ X $
only provides
$ Q $
, and network
$ Y $
, provides
$ K $
and
$ V $
. Given expressions 2.7 and 2.9, the data fusion expression reads:
$$ {\hat{\boldsymbol{V}}}_{\boldsymbol{Q}}={\boldsymbol{W}}_{\boldsymbol{O}}\sum \limits_{i=1}^kA\left(\parallel {\boldsymbol{W}}_{\boldsymbol{Q}}\boldsymbol{Q},{\boldsymbol{W}}_{\boldsymbol{K}}{\boldsymbol{K}}_i\parallel \right){\boldsymbol{V}}_i $$
where
$ A $
is an adaptive distance attention and can be either
$ {A}_{S,G} $
of
$ {A}_{L,E} $
, and
$ {W}_O $
, called the learnable parameter of the output, makes the expression able to adapt in case of trend in the measurement; it writes
$ {W}_O\in {\mathrm{\mathbb{R}}}^{q\times v} $
. A visualization of the model architecture is shown in Figure 5.
Figure 5. Schematic illustration of the data fusion architecture. Network
$ X $
provides input X and network
$ Y $
provides inputs
$ K $
and
$ V $
. Learnable parameters are
$ {W}_O $
,
$ {W}_Q $
, and
$ {W}_K $
. Attention is represented by the symbol
$ A $
without any subscript to ease the reading. The prediction at query
$ Q $
is symbolized as
$ \hat{V} $
.
The learnable parameters
$ {W}_O $
,
$ {W}_Q $
, and
$ {W}_K $
are the outputs of three multilayer perceptrons. Each multilayer perceptron reads:
$$ MLP(X)=\left\{\begin{array}{l}{H}^{(1)}=\sigma \left({W}^{(1)}X+{b}^{(1)}\right)\\ {}{H}^{(2)}=\sigma \left({W}^{(2)}{H}^{(1)}+{b}^{(2)}\right)\\ {}O=\sigma \left({W}^{(3)}{H}^{(2)}+{b}^{(3)}\right)\end{array}\right.. $$
where
$ X $
is the input matrix,
$ {W}^{(i)} $
are the hidden-layer weights matrices,
$ {b}^{(i)} $
is the bias vectors, and
$ \sigma (.) $
is the ReLU activation function. We have thus:
$$ {\boldsymbol{W}}_{\boldsymbol{O}}={MLP}_O\left(\boldsymbol{Q}\right) $$
with
$ {W}_O^{(1)}\in {\mathrm{\mathbb{R}}}^{d\times h} $
,
$ {W}_O^{(2)}\in {\mathrm{\mathbb{R}}}^{h\times h} $
,
$ {W}_O^{(3)}\in {\mathrm{\mathbb{R}}}^{h\times v} $
,
$ {b}_O^{(1)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_O^{(2)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_O^{(3)}\in {\mathrm{\mathbb{R}}}^{1\times v} $
$$ {\boldsymbol{W}}_{\boldsymbol{K}}={MLP}_K\left(\boldsymbol{K}\right) $$
with
$ {W}_K^{(1)}\in {\mathrm{\mathbb{R}}}^{d\times h}\hskip1em {W}_K^{(2)}\in {\mathrm{\mathbb{R}}}^{h\times h}\hskip1em {W}_K^{(3)}\in {\mathrm{\mathbb{R}}}^{h\times d} $
,
$ {b}_K^{(1)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_K^{(2)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_K^{(3)}\in {\mathrm{\mathbb{R}}}^{1\times d} $
$$ {\boldsymbol{W}}_{\boldsymbol{Q}}={MLP}_Q\left(\boldsymbol{Q}\right) $$
with
$ {W}_Q^{(1)}\in {\mathrm{\mathbb{R}}}^{d\times h} $
$ {W}_Q^{(2)}\in {\mathrm{\mathbb{R}}}^{h\times h} $
,
$ {W}_Q^{(3)}\in {\mathrm{\mathbb{R}}}^{h\times d} $
,
$ {b}_Q^{(1)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_Q^{(2)}\in {\mathrm{\mathbb{R}}}^{1\times h} $
,
$ {b}_Q^{(3)}\in {\mathrm{\mathbb{R}}}^{1\times d} $
.
Ultimately, we address the challenge of overfitting by implementing dropout with a probability of
$ p $
specifically applied to the attention mechanism.
2.4.1. Models overview
We highlight 12 data fusion models in the adaptive distance attention framework following expression 2.10. They differ both in terms of attention
$ {A}_{L,E} $
or
$ {A}_{S,G} $
, as well as with different assumptions simplifying expressions 2.12, 2.13, and 2.14: i) the learnable parameters of each dimension of
$ Q $
and
$ K $
are either constant or not ii) the presence or absence of the learning parameter
$ {W}_O $
, iii) both networks
$ X $
and
$ Y $
measure a physical phenomenon with identical or different spatial structures. For example, a model with attention
$ {A}_{L,E}, $
in absence of
$ {W}_O $
, and where networks
$ X $
and
$ Y $
are measuring a physical phenomenon with identical spatial structure is a data fusion approach based on OK. An overview of each model with their name, their attention, and the characteristics of their learnable parameters is given in Table 1. For readability, we designate models incorporating a kriging system like OK as “krig,” and models involving the Nadaraya–Watson kernel, such as GRNN, as “NW.” The addition of the “NN” suffix to the name signals the involvement of learnable parameters through multilayer perceptrons.
Table 1. Description of the 12 data fusion models, with their name, their attention, and the characteristics of their learnable parameters
2.5. Cases studies
This section aims at describing the three case studies of this article. It describes first the phenomena that synthetic sensor devices will measure, the construction of heterogeneous networks of mobile sensor devices, and finally the presence of several networks used for the experimentation.
For each case study, we assume a phenomenon representing ground truth to be constant in time and provided by a model or a dataset
$ M $
. We chose three case studies spanning a spectrum of complexities, ranging from simple to intricate. The complexity is related to the ground truth to be measured, and the spatial resolution of the measurements of the sensor devices.
2.5.1. Simplistic
This simplistic ground truth evolves over an area with dimensions
$ x\in \left[0;1\right] $
and
$ y\in [0;1] $
. Its spatial area is 1 unit, and its spatial resolution is
$ {\mathrm{2.5.10}}^{-5} $
unit. Its values follow the expression
$ V\left(x,y\right)={\cos}^2\left(2\pi x\right)+{\sin}^2\left(2\pi x\right) $
(Figure 6).
Figure 6. Illustration of the static two-dimensional ground truth used in case study “Simplistic.”
2.5.2. Topography
This ground truth is a subset of the 25-m spatial resolution Digital Elevation Model EU-DEM v1.1 (Copernicus, Reference Copernicus2016) over an area of 196
$ {km}^2 $
with x-coordinates between 4342031 m and 4356031 m and y-coordinates between 4085001 m and 4099001 m in the reference-system EPSG:3035 (Figure 7).
Figure 7. Illustration of the static two-dimensional ground truth used in case study “Topography.” It represents a subset of the 25-m spatial resolution Digital Elevation Model EU-DEM v1.1 over an area of 196
$ {km}^2 $
in Norway.
2.5.3. Annual hourly nitrogen dioxide concentration
This ground truth is the result of an annual average of hourly nitrogen dioxide concentration (AH
$ {NO}_2 $
) in 2019 over an area of 1026
$ {km}^2 $
over the Oslo metropolitan region resulting from the simulation using the EPISODE dispersion model (Hamer et al., Reference Hamer, Walker, Sousa-Santos, Vogt, Vo-Thanh, Lopez-Aparicio, Ramacher and Karl2020). EPISODE is a two-step model: first, a 3D Eulerian model provides a 1-
$ {km}^2 $
spatial resolution grid, and then a sub-grid model using preprocessed point and line source emissions provides
$ {NO}_2 $
concentrations at, in this case, 21209 point locations (also called “receptor points”). The spatial density of these locations is irregularly distributed: most of the information is located over the urban areas and on main roads with large sources of traffic-related
$ {NO}_2 $
emissions and strong spatial gradients in pollution patterns. Outside of these areas, the spatial density of the output is lower, with receptor points distributed at every 1 km. Instead of processing a spatial interpolation between each location to get a grid of 100-m spatial resolution over the whole area of interest, we directly exploit the receptor point data (Figure 8).
Figure 8. Illustration of the static two-dimensional ground truth used in case study “AH
$ {NO}_2 $
.” It represents the annual average of hourly nitrogen dioxide concentrations in 2019 over the Oslo metropolitan region simulated with the EPISODE dispersion model.
2.5.4. Heterogeneous networks of mobile sensor devices
This section presents the characteristics used in creating synthetic mobile sensor devices in order for them to be as representative as possible compared to environmental sensors as described in Section 2.1 and illustrated in Figure 1. We use six types of sensor devices, whose type is characterized by their spatial resolution and their measurement quality. A network is composed of
$ k $
sensor devices moving over
$ N $
predefined locations uniformly distributed over the domain for each case study. At each timestep,
$ k $
sensor devices randomly chosen among the six types of sensor devices provide one measurement each.
The sensor devices are characterized by two types of measurement spatial resolution. The first type is chosen identical to the spatial resolution of the dataset. The second type is at a coarser spatial resolution where a measurement is a spatial average over a square area. None of the sensor devices provides measurement as multi-pixel but only as a single pixel. For the case studies of the simplistic phenomena and the topography, a spatial average is processed on the ground truth. For the case study AH
$ {NO}_2 $
, the data with a coarser spatial resolution comes from the 3D-Eulerian model and data with the higher resolution comes from the sub-grid model. The characteristics of the measurement spatial resolution for the three case studies are presented in Table 2.
Table 2. Information about measurement spatial resolution for the three cases studies
a Output from the sub-grid model.
b Output from the 3d-Eulerian model.
The sensor devices are characterized by three types of measurement quality: high, medium, and low. We produce measurements
$ {V}_t^D $
for a sensor device at a specific time and location by adding uncertainty to the ground truth
$ {M}_t^D $
with spatial resolution
$ D $
, following a Normal distribution in a total error framework (Working Group on Guidance for the Demonstration of Equivalence, 2010; Lepioufle et al., Reference Lepioufle, Marsteen and Johnsrud2021). Thus, the measurements of a sensor device are given by:
$$ {V}_t^D\sim \mathbf{\mathcal{N}}\left({\beta}_0.{M}_t^D+{\beta}_1,{\sigma}_{g,t}^2+{\sigma}_{h,t}^2+{\sigma}_r^2\right) $$
Given ground truth to be perfect, its structural error is nil, and so is its standard deviation
$ {\sigma}_{h,t} $
. The standard deviation
$ {\sigma}_{g,t} $
is the parameter of the sensor device error. It is chosen proportionally to the measurements as used in Ref. (Translation of the Report on the Suitability Test of the Ambient Air Measuring System, 2007), that is,
$ {\sigma}_{g,t}={M}_t^D{\sigma}_g $
. It is usually determined as a percentage. The choice of the parameter
$ {\sigma}_g $
follows Refs. (Translation of the Report on the Suitability Test of the Ambient Air Measuring System, 2007; Directive 2008/50/EC, 2008). For instance, a reference monitoring station has
$ {\sigma}_g\le 5\% $
, and a low-cost sensor device has
$ {\sigma}_g\ge 30\% $
. In addition, we make the simplifying assumption that the sensor of the device does not exhibit any aging effect, that is,
$ {\beta}_0 $
is equal to one and
$ {\sigma}_g $
is constant over time. In our case, errors due to both external effects (e.g., meteorology, environment) and internal effects (e.g., mechanical and electronic components) are represented in a remnant error characterized by the parameters
$ {\beta}_1 $
and
$ {\sigma}_r $
. We assume the sensor devices of the first type to run on an internal system characterized as robust, the second type on a medium one, and the third on a weak one. Besides, we assume the external environment of the three case studies to be different: from gentle for the “Simplistic” case study to difficult for “AH
$ {NO}_2 $
” case study. As a consequence, the external environment affects the signal of the sensor devices by amplifying the error related to the internal system. We chose the parameters of the remnant error in a heuristic manner. Parameters describing the three types of measurement quality are given in Table 3. Remnant error parameters remain identical for the case studies “Topography” and “AH
$ {NO}_2 $
.” Nonetheless, given the lower values for case study “AH
$ {NO}_2 $
,” these parameters will get a higher impact on the signal of the sensor device. In addition, based on empirical testing, the remnant error parameters are multiplied by
$ {1.10}^2 $
for case “Simplistic” to keep the effect of the external environment gentle.
Table 3. Parameters related to the three measurement quality types
Note. Case study “Simplistic” sees its parameters
$ {\beta}_1 $
and
$ {\sigma}_r $
multiplied by
$ {1.10}^2 $
.
Finally, we describe a sensor device by its two characteristics: its spatial resolution (R) and its measurement quality (Q), to each of which we add a subscript to describe the type of characteristics: high (H), medium (M), and low (L). Thus, the six types of sensor device read
$ {R}_H{Q}_H $
,
$ {R}_H{Q}_M $
,
$ {R}_H{Q}_L $
,
$ {R}_L{Q}_H $
,
$ {R}_L{Q}_M $
, and
$ {R}_L{Q}_L $
.
2.6. Experimentation plan
In this section, we describe our experimentation. It consists of testing our model architecture, described in Section 2.4 on the three case studies described in Section 2.5.
2.6.1. Seven heterogeneous networks
For each case study, the experiment is based on seven heterogeneous networks of sensor devices, all distinct from each other. Our data fusion model requires two networks
$ X $
and
$ Y $
for the three phases: the simultaneous training and validation phases, and the evaluation phase of the prediction model. In addition, one last network is used to assess the measurement quality as it is carried out for real measurement campaigns, either with co-location or in a laboratory with a climatic chamber: every measurement of one type of sensor device is compared to a reference instrument representing a high quality point sensor device. The resulting metrics are then used as a priori information about the measurement quality of the sensor device.
2.6.2. Networks X and Y
During the training, validation, and evaluation phases, both networks
$ X $
and
$ Y $
are built-up in the same manner. They consist of 600 sensor devices moving across 1000 fixed locations. For each network X and Y, several sensor devices might occupy the same location. However, the 1000 locations of the sensor devices in
$ X $
will be different from the 1000 locations in Y. At each timestep, 100 sensor devices randomly chosen within network
$ X $
and 100 sensor devices randomly chosen within network
$ Y $
provide measurements of one variable. We have, thus,
$ q=k=100 $
and
$ v=1 $
. The network used for the calibration consists of 600 sensors representing the six measurement characteristics co-located with sensor devices with high-quality point measurements. Ground truth being constant over time, we do not use time as a dimension describing the values. Therefore, the keys
$ K $
and the queries
$ Q $
are represented in a four-dimensional space, that is, the x-coordinate (shortened as x), the y-coordinate (shortened as y), the a priori accuracy (shortened as acc), and the a priori precision (shortened as prec), thus d = 4.
2.6.3. Model architecture
For every model architecture, we use hidden layers of size
$ h=32 $
. According to Table 1, we have the models “krig” and “NW” described by 4 parameters, the models “krig2” and “NW2” with 5 parameters, the models “krig3” and “NW3” with 9 parameters, the models “krigNN” and “NWNN” with 1860 parameters, the models “krigNN2” and “NWNN2” with 2597 parameters, and the models “krigNN3” and “NWNN3” with 3945 parameters. We use a dropout of
$ p=0.1 $
. In addition, for models using
$ {A}_{L,E} $
, solving the kriging system with sensor devices of network
$ Y $
with potentially identical locations will result in nonuniqueness of the solution. We overcome this issue by using a function linalg that computes a solution to the least squares problem of the kriging system. Finally, we write the learnable parameters
$ {W}_K $
and
$ {W}_Q $
related to each dimension as
$ {W}_{.,x} $
,
$ {W}_{.,y} $
,
$ {W}_{., acc} $
, and
$ {W}_{., prec} $
where the dot determines either
$ K $
or
$ Q $
.
2.6.4. Training, validation, and evaluation
The training of the models is done using the optimization algorithm Adam (Kingma and Ba, Reference Kingma and Ba2014) with a learning rate of
$ {1.10}^{-3} $
. We use mean square error (MSE) as loss while training and validating the models. We use 200 epochs with an early exit stopping the training phase if the loss does not improve during 20 consecutive epochs with the validation dataset. During training, validation, and evaluation, the prediction is established with standardized
$ V $
,
$ Q $
, and
$ K $
. During training and validation, the losses are processed by keeping standardized outputs while this is not the case during the evaluation phase. Metrics such as RMSE, variance and coefficient of determination
$ \left({R}^2\right) $
are used to evaluate the prediction of the models.
2.6.5. Experimentation
The first part of the experiment consists of evaluating the 12 models of Section 2.4 on the three case studies described in Section 2.5 with heterogeneous sensor devices as input and with high quality point measurement data as target. The six types of sensor devices, as described in Section 2.5, are equally represented. Besides, each location of network
$ X $
can be predicted using several sets of 100 sensor devices of network
$ Y $
as input. We thus produce an ensemble of predictions for each location of network
$ X $
and evaluate the median of the ensemble during the evaluation phase. Hereafter, to enhance clarity, we use the terms single prediction and ensemble median, respectively.
The second part of the experiment focuses on highlighting and visualizing the effect of the model architecture, the sequence over time of the mobile sensor device locations, and their characteristics on the learnable parameters and the predictions. We focus on the “Topography” case study, and krigNN2 and NWNN2 as model architectures. These models provide good metrics with a reasonable amount of parameters for non-simplistic phenomena. For this experiment, the 100 sensor devices belonging to network
$ X $
can move on 1000 predetermined locations. The same applies to the 100 sensor devices belonging to network Y. Only the sequence over time of the location of the sensor devices and their characteristics change. We train four models (two krigNN2 and two NWNN2) using four distinct sequences of mobile sensors. For each of the four trained models, we produce an ensemble of predictions using network X. Finally, for each model architecture, we highlight the difference by comparing i) the maps of the learnable parameters and ii) the maps of the dispersion of the members of the ensemble. Quantifying the dispersion of the ensemble is done by producing two maps; a first one by subtracting the 5-percentile of the ensemble to the median on every point of prediction, and a second-one by subtracting the median to its 95-percentile. The first map is called the lower dispersion and the second is called the upper dispersion. Finally, iii) the maps of the metrics (RMSE and variance) between the members of the ensemble and the observation at each location. To ease the visualization, the prediction is inferred over 6400 locations uniformly distributed over the area of the case study.
2.6.6. Implementation
We developed the Python package Steams based on Pytorch (Paszke et al., Reference Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein, Antiga and Desmaison2019), and ran the experiment on a machine equipped with an Intel Core i5-9500 CPU @ 3.00GHz x 6.
3. Results and discussion
3.1. Metrics for the different data fusion models applied to the three case studies
We present the metrics of the 12 models for the 3 case studies in Tables 4–6 for the case studies “Simplistic,” “Topography,” and “AH
$ {NO}_2 $
,” respectively. Generally, involving deep neural networks in the learnable parameters
$ {W}_K $
,
$ {W}_Q $
, and
$ {W}_O $
has a positive impact on the metrics of single prediction. Nonetheless, each case study gets its proper metrics pattern: a light impact on the metrics for case study “Simplistic” with coefficient of determination going from 0.65 to 0.89, a strong impact on the metrics for case study “Topography” with coefficient of determination going from −1.09 to 0.91, and an average impact on the metrics for case study “AH
$ {NO}_2 $
” with a coefficient of determination going from −6.43 to 0.69. Furthermore, increasing the amount of parameters of a model architecture does not automatically increase the metrics. In addition, using the ensemble median increases the metrics RMSE and variance. Nonetheless, regarding metric
$ {R}^2 $
, it tends to increase this metric for positive values and worsen it for negative ones. Finally, for single prediction, the model NWNN3 provides better metrics for case study “Simplistic” and “Topography.” For the ensemble median, model NWNN3 provides better metrics for case study “Simplistic,” and both models NWNN2 and NWNN3 provide close metrics for case study “Topography.” For case study “AH
$ {NO}_2 $
” and single prediction, the model krigNN2 provides better RMSE and variance and the model NWNN2 provides a better coefficient of determination. For the ensemble median, the model krigNN provides better RMSE and variance and NWNN2 provides a better coefficient of determination.
Table 4. Metrics of the data fusion models for case study “Simplistic”. Bold values represent the best metrics.
As an illustration, we present, for each case study and based on the model with the best RMSE and variance metrics, a prediction on 6400 locations made by 100 heterogeneous sensor devices chosen randomly over the area. Case study “Simplistic” has its prediction based on model NWNN3 and is shown in Figure 9. Case study “Topography” has its prediction based on model NWNN3 and is shown in Figure 10. Finally, case study “AH
$ {NO}_2 $
” has its prediction based on model krigNN2 and is shown in Figure 11. Generally, the prediction well reproduces the phenomena presented as ground truth and keep prediction values in the same range of values of the ground truth.
Figure 9. Illustration of one prediction for the case study “Simplistic” based on the measurements of 100 sensor devices (left). Each type of sensor device is described as a symbol: circle:
$ {R}_H{Q}_H $
, triangle down:
$ {R}_H{Q}_M $
, square:
$ {R}_H{Q}_L $
, pentagon:
$ {R}_L{Q}_H $
, star:
$ {R}_L{Q}_M $
, and diamond:
$ {R}_L{Q}_L $
. The prediction is based on the model NWNN3 and is carried out at 6400 locations (middle). Ground truth on these 6400 locations is presented on the panel on the right.
Figure 10. Illustration of one prediction for the case study “Topography” based on the measurements of 100 sensor devices (left). Each type of sensor device is described as a symbol: circle:
$ {R}_H{Q}_H $
, triangle down:
$ {R}_H{Q}_M $
, square:
$ {R}_H{Q}_L $
, pentagon:
$ {R}_L{Q}_H $
, star:
$ {R}_L{Q}_M $
, and diamond:
$ {R}_L{Q}_L $
. The prediction is based on the model NWNN3 and is carried out at 6400 locations (middle). Ground truth on these 6400 locations is presented on the panel on the right.
Figure 11. Illustration of one prediction for the case study “AH
$ {NO}_2 $
” based on the measurements of 100 sensor devices (left). Each type of sensor device is described as a symbol: circle:
$ {R}_H{Q}_H $
, triangle down:
$ {R}_H{Q}_M $
, square:
$ {R}_H{Q}_L $
, pentagon:
$ {R}_L{Q}_H $
, star:
$ {R}_L{Q}_M $
, and diamond:
$ {R}_L{Q}_L $
. The prediction is based on the model krigNN2 and is carried out at 6400 locations (middle). Ground truth on these 6400 locations is presented on the panel on the right.
We show accuracy-precision diagrams to compare the metrics of the 12 models used for single prediction with the six types of sensor devices used as a priori information in Figures 12–Figure 14 for the case studies “Simplistic,” “Topography,” and “AH
$ {NO}_2 $
,” respectively. Sensor devices of high spatial resolution and high measurement quality
$ \left({R}_H{Q}_H\right) $
are chosen as reference. First, we observe that given the different case studies, the “quality” order of the different types of sensors differ. For example, a sensor device of low spatial resolution and of high measurement quality is the second best sensor device for case study “Simplistic,” and among the last ones for the case study “AH
$ {NO}_2 $
.” In the case study “AH
$ {NO}_2 $
,” a sensor device of low spatial resolution and of low measurement quality can get a better accuracy than a sensor device of low spatial resolution and of high measurement quality. Finally, we observe that models involving deep neural networks in the learnable parameters
$ {W}_K $
,
$ {W}_Q $
, and
$ {W}_O $
achieve metrics close to those from sensor devices of high spatial resolution and of medium measurement quality. Models not involving deep neural networks achieve metrics similar to a sensor device of high spatial resolution and low measurement quality for the case studies “Topography” and “AH
$ {NO}_2 $
,” and between sensor devices of low spatial resolution and high measurement quality and sensor devices of high spatial resolution and low measurement quality for the case study “Simplistic.”
Figure 12. Accuracy-precision diagram for case study “Simplistic” with both a priori measurement quality related to the 6 types of sensor devices (black circles) and the metrics of the 12 data fusion models (green stars). Some green stars represent several models with identical metrics (e.g., NWNN, krigNN2, and krigNN3).
Figure 13. Accuracy-precision diagram for case study “Topography” with both a priori measurement quality related to the 6 types of sensor devices (black circles) and the metrics of the 12 data fusion models (green stars).
Figure 14. Accuracy-precision diagram for case study “AH
$ {NO}_2 $
” with both a priori measurement quality related to the 6 types of sensor devices (black circles) and the metrics of the 12 data fusion models (green stars).
3.2. Variability of the learnable parameters from architecture krigNN2 and NWNN2 for case study “Topography”
We show the 2D representations of the learnable parameters
$ {W}_K $
and
$ {W}_O $
with sensor devices of high spatial resolution and high measurement quality as input in Figures 15 and 16, respectively. The figures represent the learnable parameters obtained using the two trained krigNN2 models and two trained NWNN2 models. Our attention models being based on the Euclidean distance, we ease the visualization, without changing any meaning, by plotting the absolute values of the learnable parameters related to their dimension. The higher the value of a learnable parameter, the higher the weight of its dimension in the distance attention. The maps of
$ {W}_{K,x} $
,
$ {W}_{K,y} $
,
$ {W}_{K, acc} $
, and
$ {W}_{K, prec} $
each have their own color scale to highlight the patterns and order of magnitude. For two trained models of identical architecture, we see their learnable parameters to have different patterns. Nonetheless, they all keep a coherent pattern distributed in space. In addition, their values respect an identical order of magnitude for each dimension. Finally, the learnable parameters corresponding to model architecture krigNN2 are constrained by its kriging system and are thus characterized by lower values than the ones corresponding to model architecture NWNN2.
Figure 15. 2D-maps of the learnable parameters
$ {W}_K $
and
$ {W}_O $
for a sensor device of high spatial resolution and high measurement quality. Two sets of learnable are presented corresponding to two krigNN2 models trained using two different sequences of sensor devices evolving on a same network
$ X $
and
$ Y $
. From top to bottom:
$ {W}_{K,x} $
,
$ {W}_{K,y} $
,
$ {W}_{K, acc} $
,
$ {W}_{K, prec} $
, and
$ {W}_O $
.
Figure 16. 2D-maps of the learnable parameters
$ {W}_K $
and
$ {W}_O $
for a sensor device of high spatial resolution and high measurement quality. Two sets of learnable parameters are presented corresponding to two NWNN2 models trained using two different sequences of sensor devices evolving on a same network
$ X $
and
$ Y $
. From top to bottom:
$ {W}_{K,x} $
,
$ {W}_{K,y} $
,
$ {W}_{K, acc} $
,
$ {W}_{K, prec} $
, and
$ {W}_O $
.
We then show the 2D-maps of the dispersion of the ensemble of prediction obtained from the two trained krigNN2 models in Figure 17 and the two trained NWNN2 models in Figure 18. Each ensemble is composed of around 600 members. The upper figures show the lower dispersion, and the lower figures show the upper dispersion. From one model architecture to another, we see two distinct dispersion patterns. Nevertheless, when employing an identical model architecture, we observe a comparable dispersion pattern, despite a slight variance in magnitude. Furthermore, for each trained model, the upper dispersion and the lower one have almost symmetric patterns. Only the isolated patches with higher values alter the symmetry.
Figure 17. 2D-maps of the lower dispersion (top) and upper dispersion (bottom). Two sets of dispersion are presented corresponding to two krigNN2 models trained using two different sequences of sensor devices evolving on a same network X and Y.
Figure 18. 2D-maps of the lower dispersion (top) and upper dispersion (bottom). Two sets of dispersion are presented corresponding to two NWNN2 models trained using two different sequences of sensor devices evolving on a same network X and Y.
Finally, we present the 2D-maps of the metrics between the members of the ensemble obtained from the two trained krigNN2 models and the two trained NWNN2 models against the observations, respectively, in Figures 19 and 20. The upper panels show the RMSE and the lower panels show the variance. Identically to the dispersion 2D-maps, we see two distinct patterns from one model architecture to another. In addition, the trained models with identical architecture provide similar patterns with a small difference in the order of magnitude. Furthermore, for each trained model, contrarily to 2D-maps of metric RMSE described by local variability, 2D-maps of metric variance have larger patterns that match the asymmetry between the dispersion 2D-maps. Finally, given the global metrics in Table 5, where the RMSE is around 32 m and variance around 550 m2 for both krigNN2 and NWNN2, these 2D-maps of the metrics highlight local but large errors in the prediction; for instance, the 2D-map visualizing the RMSE of the krigNN2 model can reach 200 m and 120 m for NWNN2, and the 2D-map variance of the krigNN2 and NWNN2 models can reach 1400 m2.
Figure 19. 2D-maps of metrics RMSE (top) and variance (bottom). Two sets of dispersion are presented corresponding to two krigNN2 models trained using two different sequences of sensor devices evolving on a same network X and Y.
Figure 20. 2D-maps of metrics RMSE (top) and variance (bottom). Two sets of dispersion are presented corresponding to two NWNN2 models trained using two different sequences of sensor devices evolving on a same network X and Y.
Table 5. Metrics of the data fusion models for case study “Topography”. Bold values represent the best metrics.
Table 6. Metrics of the data fusion models for case study “AH
$ {NO}_2 $
”. Bold values represent the best metrics.
3.3. Discussion
Adaptive distance attention allows the fusion of the measurements collected by sparse, heterogeneous and mobile sensor devices and the prediction of values at locations with no measurements. We tested this method on three static phenomena over time with different complexities. For each case study, a first network of 100 moving and heterogeneous sensor devices were deployed and trained using a second network of 100 moving high quality sensor devices. In general, the results are positive. By including deep learning models into learnable parameters, we improved the metrics from the baseline models OK and GRNN, called “krig” and “NW” in this study. For the three case studies, accuracy-precision diagrams highlight the capability of adaptive distance attention to provide predictions at arbitrary locations with a quality close to sensor devices of medium quality, that is, with an uncertainty of 10% of the signal. Furthermore, the method allows for automatically incorporating the way measurements are weighted according to their a priori quality without using any methods such as Kalman filter or data assimilation. Distance attention using the Nadaraya–Watson kernel provides metrics in the same order of magnitude as the attention based on the kriging system; while solving the kriging system involves a matrix inversion, the Nadaraya–Watson kernel is a good alternative to alleviate processing cost for data fusion of sparse data.
In this study, we assume the existence of 100 sensor devices of high quality at high spatial resolution used as targets to train the data fusion model. This choice is useful to test our data fusion model architecture; it represents nonetheless a high instrumental cost for a measurement campaign. Reducing the instrumentation cost might be done by training a model with sensor devices of different qualities and different spatial resolutions as targets. For this purpose, future work will focus on connecting the raw signal output of the sensors described as level 0, following Ref. (Schneider et al., Reference Schneider, Bartonova, Castell, Dauge, Gerboles, Hagler, Huglin, Jones, Khan, Lewis, Mijling, Müller, Penza, Spinelle, Stacey, Vogt, Wesseling and Williams2019), to both their external environment and their internal system and bring these variables as keys into the data fusion model. This approach will allow the modeling of the ageing effect of the sensor and the hardware.
Our study focuses on evaluating a trained model with observations belonging to the same bounding area as the training and testing datasets. To enable the use of the trained model with heterogeneous sensors in areas outside of this domain we will test other keys
$ K $
connected to the phenomena of interest. In the case of “AH
$ {NO}_2 $
,” and in addition to the coordinates, such auxiliary datasets could include information on the underlying emissions (Grythe et al., Reference Grythe, Lopez-Aparicio, Høyem and Weydahl2022), the characteristics of the cities from OpenStreetMap as in Steininger et al. (Reference Steininger, Kobs, Zehe, Lautenschlager, Becker and Hotho2020) and meteorological information. Further investigation will be required to test the potential of our method from extrapolation to transfer learning for cities with difference ranging from subtle to significant; for example, it would be interesting to start testing the trained model to predict “AH
$ {NO}_2 $
” on highways connected to the Oslo metropolitan area but outside this area, then to use the trained model to predict “AH
$ {NO}_2 $
” over other cities within Norway, and finally to test the trained model to predict “AH
$ {NO}_2 $
” in cities worldwide.
Our case studies assume phenomena constant in time. This choice is useful to test our data fusion model architecture. Adapting our method for the prediction of time-dependent phenomena will require adding variables related to time into the keys
$ K $
. Keeping in mind our interest in predicting hourly urban air quality, we will first follow the work of Stojanović et al. (Reference Stojanović, Kleut, Davidović, Jovašević-Stojanović, Bartonova and Lepioufle2023) by using B-splines to encode periodic time-related features related to the human behavior. Then, we will test time-embedding methods, such as Kazemi et al. (Reference Kazemi, Goel, Eghbali, Ramanan, Sahota, Thakur, Wu, Smyth, Poupart and Brubaker2019), on meteorological variable influencing air quality, such as temperature, wind, and relative humidity. Finally, for forecast purposes, we will adapt the transformer architecture (Lin et al., Reference Lin, Wang, Liu and Qiu2022) to our method.
Quantifying the uncertainty automatically is crucial for optimizing measurement campaigns and sensor selection. In our study, we employ ensemble prediction to create error maps. However, this approach has a significant computational cost and provides post-measurement insights. Our future work will focus on refining the model architecture for real-time and cost-effective error prediction. We will follow the work of Tagasovska and Lopez-Paz (Reference Tagasovska and Lopez-Paz2019), where the uncertainty in deep neural networks is estimated using a single model and simultaneous quantile regression as a loss function. This method effectively captures all conditional quantiles, enabling well-calibrated prediction intervals with complex characteristics such as asymmetry, multimodality, and heteroscedasticity.
We assume that measurement campaigns are random sequences of sensor devices deployed at different locations, with different measurement qualities, and different spatial resolutions following predefined characteristics. Our results show that the patterns of learnable parameters differ from one measurement campaign to another; contrary to the constant pattern from feature extraction (Steininger et al., Reference Steininger, Kobs, Zehe, Lautenschlager, Becker and Hotho2020), adaptive distance attention extracts representative information of the phenomena that are ad hoc to one measurement campaign. Nonetheless, even though metrics of the same model architecture are of the same order of magnitude, some local errors characterized as spikes can occur. In a measurement campaign, localizing the areas with potentially significant errors is useful to plan further campaigns and minimize these errors. Highlighting, a posteriori, the locations of these errors with ensemble prediction is possible but has a processing cost. Avoiding the local errors while keeping a reasonable processing cost might be possible by planning the measurement campaign to catch relevant information while minimizing local metrics. For this purpose, future studies should focus on designing the measurement campaign workflow (Vasiljević et al., Reference Vasiljević, Vignaroli, Bechmann and Wagner2020) of the sensor device while letting them adapt to any external or internal constraints using reinforcement learning (Zhou et al., Reference Zhou, Chen and Zou2020). In doing so, it is important to limit the computational requirements reasonable while keeping models that allow accurate predictions. Finally, we will take the direction of combining this approach with intelligent instrumentation design (Ballard et al., Reference Ballard, Brown, Madni and Ozcan2021) to help designing new sensor devices to reach better metrics, for instance, in the case study of “AH
$ NO2 $
.”
4. Conclusion
We describe the methodology and demonstrate the potential of an adaptive distance attention technique that allows for i) the fusion of observations made by sparse, heterogeneous, and mobile sensor devices; ii) the prediction of values at locations with no measurements; and iii) the automatic weighting of the measurements according to a priori quality information about the sensor device without using any methods of data assimilation.
We integrate both OK and a GRNN into this attention with their learnable parameters based on deep learning architectures. We evaluate this method using three static phenomena with different complexities: a case related to a simplistic phenomenon, topography over an area of 196
$ {km}^2 $
and to the annual hourly
$ {NO}_2 $
concentration in 2019 over the Oslo metropolitan region (1026
$ {km}^2 $
).
We simulate networks of 100 synthetic sensor devices with six characteristics related to measurement quality and measurement spatial resolution. This approach allows us to generate a set of sensor devices describing reference monitoring stations, low-cost sensor devices, and pixels of satellites.
Outcomes are promising: we significantly improve the metrics from baseline geostatistical models without using any methods of data assimilation.
For the three case studies, accuracy-precision diagrams highlight the capability of adaptive distance attention to provide predictions at arbitrary locations with a quality close to sensor devices of medium quality, that is, with an uncertainty of 10% of the signal of ground truth.
In addition, distance attention using the Nadaraya–Watson kernel provides as good metrics as the attention based on the kriging system enabling the possibility to alleviate the processing cost for fusion of sparse data.
Finally, fusing heterogeneous sensor devices with adaptive distance attention can be used for measurement campaigns of local phenomena in isolated areas. The results are encouraging, and we are planning to continue adapting this approach to space-time phenomena evolving in complex areas.
Author contribution
Conceptualization, methodology, and software: J.M.L. Data curation: P.D.H., P.S., R.Ø., and I.V. Writing—original draft: J.M.L. Writing—review and editing: J.M.L. and P.S. Funding acquisition: A.T., T.V.C., J.M.L., P.S., and M.W. All authors approved the final submitted draft.
Competing interest
The authors declare none
Data availability statement
The 25-m spatial resolution Digital Elevation Model EU-DEM v1.1 is available at https://www.eea.europa.eu/data-and-maps/data/copernicus-land-monitoring-service-eu-dem. The Python package Steams is available at https://pypi.org/project/steams/.
Ethics statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by grants from the Research Council of Norway (project number 322473) and the National Centre for Research and Development of Poland (Grant No. NOR/POLNOR/HAPADS/0049/2019-00). Additional partial funding provided by the European Space Agency within the framework of the CitySatAir project (4000131513/20/I-DT), by the Norwegian Research Council in the URBANITY project (321118), and the European Union in the CitiObs project (101086421), is gratefully acknowledged.
Open access
