4.1 The symmetric subgame PM/PM

Consider first the subgame in which the decision about industrial production and abatement is taken by the owner of each firm (i.e., firms are profit maximisers) at the market stage of the game, i.e., the PM scheme works as if the bonus set by the owner to the manager were equal to zero. The profit function of firm i is:

(1)\begin{equation}{\pi _i} = ({1 - {q_i} - {q_j}} ){q_i} - t({{q_i} - {k_i}} )- \frac{{{k_i}^2}}{2},\;i = 1,2,\;i \ne j.\end{equation}

At the market stage of the game, owners choose both the optimal amount of output coming from industrial production and abatement to maximise profits. Maximisation of equation (1) with respect to ${q_i}$ and ${k_i}$ yields the following set of first-order conditions:

(2)\begin{equation}\bar{q}_i^{{\rm PM/PM}} = \frac{1}{2}({1 - {q_j} - t} ),\;\bar{k}_i^{{\rm PM/PM}} = k_i^{{\rm PM/PM}} = t,\;i = 1,2,\;i \ne j.\end{equation}

where the superscript PM/PM stands for profit maximisation of both firms. The solution of the system of output reaction functions $\bar{q}_i^{{\rm PM/PM}}\;(i = 1,2,\;i \ne j)$ in equation (2) leads firm i to produce the following pre-tax stage equilibrium quantity of product of variety i as a function of the emissions tax $t.$ That is,

(3)\begin{equation}q_i^{{\rm PM/PM}} = \frac{1}{3}({1 - t} ).\end{equation}

Using equation (3) and the first-order condition $k_i^{{\rm PM/PM}} = t$ in equation (2), one can directly obtain the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm PM/PM}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm PM/PM}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm PM/PM}}})$ and environmental damage $({\rm E}{{\rm D}^{{\rm PM/PM}}})$ as a function of the tax rate when both firms are profit maximisers (reported in online appendix B), allowing us to obtain social welfare under PM/PM $({\rm S}{{\rm W}^{{\rm PM/PM}}} = {\rm P}{{\rm S}^{{\rm PM/PM}}} + {\rm C}{{\rm S}^{{\rm PM/PM}}} + {\rm T}{{\rm R}^{{\rm PM/PM}}} - {\rm E}{{\rm D}^{{\rm PM/PM}}})$, which is reported in lemma 1.

Lemma 1 The social welfare function under PM/PM as a function of the tax rate is given by:

(4)\begin{equation}{\rm S}{{\rm W}^{{\rm PM}/{\rm PM}}} = \frac{4}{9} - \frac{2}{9}{t} - \frac{{11}}{9}{{t}^2} + {g}\left( { - \frac{2}{9} + \frac{{16}}{9}{t} - \frac{{32}}{9}{{t}^2}} \right).\end{equation}

At the first stage of the subgame (the government stage), the government levies an emissions tax with the aim of maximising social welfare. Proposition 1 shows the extent of the welfare maximising tax rate ${t^{{\ast {\rm PM/PM}}}}$ and the condition under which the optimal tax rate in the subgame PM/PM is positive (see proofs of lemma 1 and proposition 1 in online appendix B).

Proposition 1 The welfare-maximising tax rate under PM/PM is given by the following expression, which is positive if and only if $g > 0.125$:

(5)\begin{equation}{t^{\mathrm{\ast PM/PM}}} = \frac{{8g - 1}}{{32g + 11}}.\end{equation}

Using the optimal tax rate in equation (5), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast PM/PM}} = (4(2g + 1)/(32g + 11)) > 0$, abatement $k_i^{\mathrm{\ast PM/PM}} = ((8g - 1)/(32g + 11)) > 0\;g > 0.125$, and emissions $q_i^{\mathrm{\ast PM/PM}} - k_i^{\mathrm{\ast PM/PM}} > 0$. Finally, inserting back the optimal tax ${t^{\mathrm{\ast PM/PM}}}$ into the profit function in equation (1), one gets equilibrium profits under PM/PM, that is:

(6)\begin{equation}\pi _i^{\mathrm{\ast PM/PM}} = \frac{{192{g^2} + 112g + 33}}{{2{{(32g + 11)}^2}}}.\end{equation}

4.2. The symmetric subgame GD/GD

Let us now consider the case in which owners delegate output and abatement decisions to their own managers by designing a delegation contract that includes an environmental component based on emissions (GD), i.e., firms are ‘green’ delegated at the market stage of the game. In a managerial delegation model framed in a strategic competitive context, each firm consists of owners who control the firm and a manager whose decisions are based on an incentive contract that the corresponding owner designs. Managers get a publicly observed contract whose remuneration is ${R_i} = \mathrm{{\rm A}} + \mathrm{{\rm B}}{U_i} \ge 0$, where $\mathrm{{\rm A}} \ge 0$ is the fixed salary component of the manager's compensation, $\mathrm{{\rm B}} \ge 0$ is a constant parameter, and ${U_i}$ is the manager $i$'s utility. Without loss of generality, we set $\mathrm{{\rm A}} = 0$ and $\mathrm{{\rm B}} = 1$ henceforth. Each manager's compensation structure is proportional to a linear combination of profit and an incentive based on emissions. The objective function of the manager of the polluting firm i takes a form like those introduced by Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987), and Fershtman and Judd (Reference Fershtman and Judd1987) in their pioneering contributions. The equation is:

(7)\begin{equation}{U_i} = {\pi _i} + {b_i}{e_i},\;i = 1,2,\;i \ne j,\end{equation}

weighting profits and emissions instead of profits and sales. In equation (7), ${\pi _i}$ is the profit function defined in equation (1), and ${b_i} > 0\; ( < 0)$ is the incentive (disincentive) designed by the owner regarding quantity and abatement (i.e., emissions) chosen by the manager, which determines actual pollution of firm i, that is, ${e_i} = {q_i} - {k_i}$. Therefore, the maximisation of the utility function in equation (7) by manager i with respect to ${q_i}$ and ${k_i}$ at the market stage of the subgame leads to the following set of first-order conditions:Footnote ⁸

(8)\begin{equation}\bar{q}_i^{{\rm GD/GD}} = \frac{1}{2}({1 - {q_j} - t + {b_i}} ),\;\bar{k}_i^{{\rm GD/GD}} = k_i^{{\rm GD/GD}} = t - {b_i},\;i = 1,2,\;i \ne j,\end{equation}

where the superscript GD/GD stands for the ‘green’ delegation of both managers. The solution of the system of output reaction functions $\bar{q}_i^{{\rm GD/GD}}$ $(i = 1,2,\;i \ne j)$ in equation (8) gives the following pre-tax stage equilibrium output as a function of the emissions tax t and the bonuses ${b_i}$ and ${b_j}$. That is:

(9)\begin{equation}q_i^{{\rm GD/GD}} = \frac{1}{3}({1 - t + 2{b_i} - {b_j}} ),\;i = 1,2,\;i \ne j.\end{equation}

A direct comparison between equations (2) and (8) reveals that the ‘green’ contract promotes industrial production (as expected) and reduces abatement due to the design of the executive remuneration at the bonus stage (based on emissions instead of sales), apparently working at first glance as an anti-ecological device at the pre-tax stage compared to the case of profit maximisation $({b_i} = 0)$.

However, this section will show that the design of the GD contract by the owner allowing the ‘green’ manager to produce more and abate less than the owner under the PM contract, is such that the welfare-maximising emissions tax levied by the government at the government stage under GD goes beyond the corresponding value under PM. This eventually implies that equilibrium production and abatement at the post-tax stage of the game under GD are the same as equilibrium production and abatement at the post-tax stage of the game under PM,Footnote ⁹ allowing the same level of aggregate emissions and environmental damage to be achieved.

This policy-driven mechanism – based on a transfer of resources flowing from firms to the public authority – allows the government to perfectly compensate the increased emissions with a larger ad hoc taxation that lowers production and increases abatement under GD. Indeed, the difference between the optimal emissions tax rate under GD and the optimal emissions tax rate under PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager who is remunerated through an incentive based on emissions. This implies that the GD contract is not anti-ecological compared to the PM contract and there is no trade-off between employment (production) and social welfare in this case (see the welfare analysis in the online appendix for a thoughtful discussion of this issue).

A relevant effect of the emissions tax is to increase marginal costs and reduce equilibrium profits of the GD strategy below the equilibrium profit of the PM strategy. The former, however, will become a dominant strategy so that (GD, GD) will be the Pareto inefficient Nash equilibrium of the GD game if the public awareness towards environmental quality is high enough. Note that we are considering total pollution and the corresponding environmental damage as the main indexes to evaluate the ‘greenness’ of a managerial contract. Thus, the GD contract reduces both below the corresponding values obtained through the SD contract under abatement (see the welfare analysis in the online appendix for a thoughtful discussion of the post-tax equilibrium values of environmental damage, emissions tax, consumer's surplus, profits and social welfare under SD/SD, GD/GD and PM/PM).

Substituting equation (9) and $k_i^{{\rm GD/GD}} = t - {b_i}$ in equation (8) into the profit function in equation (1) allows us to get the expression of firm $i$'s profit as a function of the managerial incentives ${b_i}$ and ${b_j}$. Therefore, at the bonus stage owner i maximises profits with respect to ${b_i}$, which leads to the following reaction functions in the bonus space:

(10)\begin{equation}\bar{b}_i^{{\rm GD/GD}} = \frac{1}{{13}}({1 - t - {b_j}} ),\;i = 1,2,\;i \ne j.\end{equation}

From equation (10), it is clear that ${b_i}$ and ${b_j}$ are strategic substitutes,Footnote ¹⁰ i.e., an increase in executive remuneration in firm j reduces executive remuneration in firm i, and the symmetric equilibrium values of both bonus and abatement of player i as a function of the tax rate are:

(11)\begin{equation}b_i^{{\rm GD/GD}} = \frac{{1 - t}}{{14}}\;{\rm and}\;k_i^{{\rm GD/GD}} = \frac{{15t - 1}}{{14}}.\end{equation}

Making use of equation (11), further substitutions directly yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/GD}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/GD}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm GD/GD}}})$, and environmental damage $({\rm E}{{\rm D}^{{\rm GD/GD}}})$ as a function of the tax rate when both firms are ‘green’ delegated (reported in online appendix B), allowing us to get social welfare under GD/GD $({\rm S}{{\rm W}^{{\rm GD/GD}}} = {\rm P}{{\rm S}^{{\rm GD/GD}}} + {\rm C}{{\rm S}^{{\rm GD/GD}}} + {\rm T}{{\rm R}^{{\rm GD/GD}}} - {\rm E}{{\rm D}^{{\rm GD/GD}}})$, which is reported in lemma 2.

Lemma 2 The social welfare function under GD/GD as a function of the tax rate is given by:

(12)\begin{equation}{\rm S}{{\rm W}^{{\rm GD}/{\rm GD}}} = \frac{{89}}{{196}} - \frac{5}{{98}}{t} - \frac{{275}}{{196}}{{t}^2} + {g}\left( { - \frac{{18}}{{49}} + \frac{{120}}{{49}}{t} - \frac{{200}}{{49}}{{t}^2}} \right).\end{equation}

At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 2 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm GD}}}$ and the condition under which the optimal tax rate in the subgame GD/GD is positive (see proofs of lemma 2 and proposition 2 in online appendix B).

Proposition 2 The welfare-maximising tax rate under GD/GD is given by the following expression, which is positive if and only if $g > 0.020833$:

(13)\begin{equation}{t^{\mathrm{\ast GD/GD}}} = \frac{{48g - 1}}{{5({32g + 11} )}}.\end{equation}

Using the optimal tax rate in equation (13), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast GD/GD}} = (4(2g + 1)/(32g + 11)) > 0$, executive remuneration $b_i^{\mathrm{\ast GD/GD}} = (4(2g + 1)/(5(32g + 11))) > 0$, abatement $k_i^{\mathrm{\ast GD/GD}} = ((8g - 1)/(32g + 11)) > 0$ for any $g > 0.020833$, and emissions $q_i^{\mathrm{\ast GD/GD}} - k_i^{\mathrm{\ast GD/GD}} > 0$. Finally, inserting back the optimal tax ${t^{\mathrm{\ast GD/GD}}}$ into the profit function in equation (1), one gets equilibrium profits under GD/GD. That is:

(14)\begin{equation}\pi _i^{\mathrm{\ast GD/GD}} = \frac{{192{g^2} + 96g + 25}}{{2{{(32g + 11)}^2}}}.\end{equation}

A direct comparison amongst the relevant equations of the subgames PM/PM and GD/GD allows us to conclude that $\pi _i^{\mathrm{\ast GD/GD}} < \pi _i^{\mathrm{\ast PM/PM}}$, whereas the post-tax equilibrium amount of industrial production and abatement are identical in both cases. Indeed, though the ‘green’ manager chooses to abate a smaller amount of pollution in comparison to the profit maximising firm, the pre-tax output under GD/GD is larger than the pre-tax output under PM/PM due to the design of the incentive contract through the manager's executive remuneration (bonus) chosen by the owner, so that the optimal environmental tax rate is higher under GD. Indeed, a direct comparison between equation (5) and (13) allows us to observe ${t^{\mathrm{\ast GD/GD}}} > {t^{\mathrm{\ast PM/PM}}}$ for any g. This implies, ceteris paribus, that the equilibrium pre-tax consumer surplus and total revenue when designing GD are larger than in the PM/PM case, thus causing the society under GD/GD to be willing to pay a larger amount of environmental taxes than under PM/PM. However, as the difference between the optimal emissions tax rate under GD/GD and the optimal emissions tax rate under PM/PM is exactly equal to the incentive designed by the owner about the emissions chosen by the manager, the post-tax equilibrium amounts of production and abatement are the same under both contracts, and profits under GD/GD are lower than profits under PM/PM as the post-tax marginal costs are larger in the former case.

4.3 The asymmetric subgame GD/PM

To determine the owners' endogenous choice regarding whether to delegate via a ‘green’ contract based on emissions or be a profit maximiser at the pre-play stage (or contract stage), one should evaluate the outcomes of the asymmetric subgame in which one firm, say firm 1, is a ‘green’-delegated firm $({b_1} \ne 0)$, and the rival, firm 2, is still profit maximising $({b_2} = 0)$. The optimisation problems of the GD player and the PM player at the market stage provide the first-order conditions as in equation (8) for firm 1 and as in equation (2) for firm 2. Solving the system of output reaction functions, one obtains the quantities produced by both firms as a function of the tax rate and the bonus of the ‘green’ delegated firm 1. That is:

(15)\begin{equation}\bar{q}_1^{{\rm GD/PM}} = \frac{1}{3}({1 - t + 2{b_1}} )\;{\rm and}\;\bar{q}_2^{{\rm GD/PM}} = \frac{1}{3}({1 - t - {b_1}} ).\end{equation}

Substituting equation (15) and the expression of $k_i^{{\rm GD/GD}}$ in equation (8) into the profit function of firm 1, one obtains the expression of firm 1's profits as a function of the managerial incentive. At the bonus stage, the owner of firm 1 maximises profits with respect to ${b_1}$. This gives the optimal bonus $b_1^{{\rm GD/PM}} = (1/13)({1 - t} )$, so that the equilibrium expressions of quantity and abatement of firm 1 and firm 2 as a function of the tax rate are:

(16)\begin{equation}q_1^{{\rm GD/PM}} = \frac{5}{{13}}({1 - t} ),\;q_2^{{\rm GD/PM}} = \frac{4}{{13}}({1 - t} )\;{\rm and}\;k_1^{{\rm GD/PM}} = \frac{1}{{13}}({14t - 1} ),\;k_2^{{\rm GD/PM}} = t.\end{equation}

Further substitutions by making use of equation (16) yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/PM}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/PM}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm GD/PM}}})$ and environmental damage $({\rm E}{{\rm D}^{{\rm GD/PM}}})$ as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under GD/PM $({\rm S}{{\rm W}^{{\rm GD/PM}}} = {\rm P}{{\rm S}^{{\rm GD/PM}}} + {\rm C}{{\rm S}^{{\rm GD/PM}}} + {\rm T}{{\rm R}^{{\rm GD/PM}}} - {\rm E}{{\rm D}^{{\rm GD/PM}}})$, reported in lemma 3.

Lemma 3 The social welfare function under GD/PM as a function of the tax rate is given by:

(17)\begin{equation}{\rm S}{{\rm W}^{{\rm GD}/{\rm PM}}} = \frac{{76}}{{169}} - \frac{{22}}{{169}}{t} - \frac{{223}}{{169}}{{t}^2} + {g}\left( { - \frac{{50}}{{169}} + \frac{{360}}{{169}}{t} - \frac{{648}}{{169}}{{t}^2}} \right).\end{equation}

At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 3 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm PM}}}$ and the condition under which the optimal tax rate in the subgame GD/PM is positive (see proofs of lemma 3 and proposition 3 in online appendix B).

Proposition 3 The welfare-maximising tax rate under GD/PM is given by the following expression, which is positive if and only if $g > 0.06111$:

(18)\begin{equation}{t^{\ast {\rm GD}/{\rm PM}}} = \frac{{180g - 11}}{{648g + 223}}.\end{equation}

Using the optimal tax rate in equation (18), one obtains the equilibrium quantities of industrial production $q_1^{\ast {\rm GD}/{\rm PM}} = (90(2g + 1)/(648g + 223)) > 0,\;q_2^{\ast {\rm GD}/{\rm PM}} = ((72(2g \,{+}\, 1))/(648g \,{+}\, 223)) > 0$, executive remuneration $b_1^{\ast {\rm GD}/{\rm PM}} = ((18(2g \,{+}\, 1))/ (648g + 223)) > 0$, abatement $k_1^{\ast {\rm GD}/{\rm PM}} = ((144g - 29)/(648g + 223)) > 0$ for any $g > 0.20138, k_2^{{\ast {\rm GD}}/{\rm PM}} \,{=}\, ((180g \,{-}\, 11)/(648g \,{+}\, 223)) > 0$ for any $g > 0.06111$, and emissions $q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}} > 0$ and $q_2^{\ast {\rm GD}/{\rm PM}} - k_2^{\ast {\rm GD}/{\rm PM}} > 0$ for any $0.06111 < g < 2.305$. Finally, inserting the optimal tax ${t^{\ast {\rm GD}/{\rm PM}}}$ back into the profit function in equation (1), one gets equilibrium profits under GD/PM for firm 1 and firm 2, respectively:

(19)\begin{equation}\pi _1^{\ast {\rm GD}/{\rm PM}} = \frac{{82944{g^2} + 46584g + 12757}}{{2{{(648g + 223)}^2}}},\quad \pi _2^{\ast {\rm GD}/{\rm PM}} = \frac{{73872{g^2} + 37512g + 10489}}{{2{{(648g + 223)}^2}}}.\end{equation}

4.4. The owners' endogenous choice: the ‘green’ delegation game (GD versus PM)

By using the firms' profits equations given by the expressions in equations (6), (14) and (19), one can get the payoff matrix reported in table 1 for the GD game (GD versus PM). The endogenous choice of firms' owners between being ‘green’ delegated (through the design of a managerial contract based on emissions instead of sales) and profit maximisers is played at the pre-play stage or contract stage of the game.

Table 1. The ‘green’ delegation game under abatement (payoff matrix): GD versus PM

To satisfy the technical conditions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is confined to the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.20138 < g < 2.305$. The former inequality bounds from below the parameter region, requiring that the societal awareness of a clean environment should be high enough to ensure positive levels of pollution abatement for the managerial firm in the asymmetric subgame, in which the owner of one firm designs a delegation contract based on emissions to its own manager (GD), and the rival is profit maximising (PM) under abatement. The latter inequality bounds from above the parameter region, requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.

To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2$, $i \ne j$:

(20)\begin{align}{\Delta }{\pi _a} &= \pi _i^{\ast {\rm GD}/{\rm PM}} - \pi _i^{\ast {\rm PM}/{\rm PM}},\quad {\Delta }{\pi _b} = \pi _i^{\ast {\rm PM}/{\rm GD}} - \pi _i^{\ast {\rm GD}/{\rm GD}}\quad {\rm and}\notag\\ {\Delta }{\pi _c} &= \pi _i^{\ast {\rm PM}/{\rm PM}} - \pi _i^{\ast {\rm GD}/{\rm GD}}.\end{align}

An analytical inspection of the expressions in equation (20) reveals that ${\Delta }{\pi _a}\frac{\lt}{\gt}0$ if $0.20138 < g\frac{\lt}{\gt}0.37,\;{\Delta }{\pi _b} < 0$ and ${\Delta }{\pi _c} > 0$ for any $0.20138 < g < 2.305$, from which one can obtain Result 1 (see proof in online appendix B).

First, we note that asymmetric equilibria are prevented as the model does not include elements affecting one firm differently from the rival. The economic intuition of the Nash equilibrium outcomes of the GD game can be carried out following the narrative of the cases detailed in Result 1, starting from low values of the societal awareness towards a clean environmental quality (alternatively, against the – severe or mild – environmental damages caused by industrial production). If $0.20138 < g < 0.37$, there are multiple pure-strategy Nash equilibria in which the PM payoff dominates GD. When g is sufficiently low, the optimal tax rates under PM and GD are low. As ${t^{\mathrm{\ast GD}/{\rm GD}}} > {t^{\mathrm{\ast PM}/{\rm PM}}}$, profits under GD/GD are smaller than profits under PM/PM, though the post-tax equilibrium values of industrial production and abatement are the same in both cases. In addition, in the GD scenario, some resources should also be devoted to executive remuneration, but the amount of the optimal emissions tax at the equilibrium exactly compensates the reduced abatement of the ‘green’ manager due to the incentives designed by the owner through a contract based on emissions.

The combination of the effects within this range of values of g implies a drop in profits in all (symmetric and asymmetric) strategic profiles following an increase in g, as the negative effects on profits of the reduction in the amount of industrial production overcomes the positive effects due to the increase in the market price. However, the percentage reduction in profits is larger under PM than under GD in both symmetric and asymmetric subgames. This is partly because production under GD in the asymmetric subgame is larger than under PM.

In addition, ceteris paribus, the overall burden of the emissions tax under GD is larger than under PM, and this provides an incentive for firms not to deviate toward GD if the rival also chooses to be a ‘green’-delegated firm. No dominant strategies exist in this case. Definitively, the outcome of the game is a priori uncertain. In fact, on the one hand, each player is interested in PM if the rival chooses not to be ‘green’ delegated, because everyone would like to play PM. On the other hand, no one is willing to play GD if the rival plays PM, as no one wants to be the sole player to get lower profits. Again, no one would like to make decisions that they might regret, but no one can foresee the rival's decisions (this is because firms are playing a simultaneous non-cooperative game).

It could happen, however, that the two players make non-consistent choices: if someone chooses to play GD to avoid losing the opportunity to get higher profits and the rival chooses PM to reduce the tax burden, players could end up in a situation in which only one is ‘green’ delegated, representing for both an unsatisfactory outcome, as everyone could be better off with a different choice.

Differently, if decisions were compatible, both players would choose to be profit maximisers if they are willing to reduce the tax burden in a context in which social awareness against pollution is not sufficiently high, thus achieving a Pareto-efficient outcome. Players could also make compatible decisions ensuring a sub-optimal result, and thus they can both choose to be ‘green’ delegated if they are willing to avoid being the sole PM player experiencing the worst outcome.

In this context, however, players are interested in agreeing to be PM. Furthermore, by choosing PM, everyone becomes interested in complying with the non-binding agreement, as no one would have the incentive to deviate towards GD. Though the game is non-cooperative, both players have an incentive to coordinate towards PM by not designing a managerial delegation contract based on emissions.

If $0.37 < g < 2.305$, the comparison between profits under GD and PM supports the strategic profile GD. Indeed, the percentage reduction in profits under PM is larger than under GD as g increases. This is because, in the asymmetric subgame GD/PM, the GD firm produces more and abates less than the PM firm due to the design of the contract based on emissions so that $\pi _1^{\mathrm{\ast GD}/{\rm PM}} > \pi _2^{\mathrm{\ast GD}/{\rm PM}}$. The optimal emissions tax in the asymmetric subgame GD/PM is set at an intermediate value between the symmetric subgames GD/GD (the highest) and PM/PM (the lowest), so that the government is not able induce the GD firm to sufficiently increase pollution abatement in the asymmetric case. Therefore, though in the asymmetric subgame the GD firm gets a higher tax burden $\left({t^{\ast {\rm GD}/{\rm PM}}}\left(q_1^{\ast {\rm GD}/{\rm PM}} - k_1^{\ast {\rm GD}/{\rm PM}}\right)\right)$ than the PM firm $\left({t^{\mathrm{\ast GD}/{\rm PM}}}\left(q_2^{\mathrm{\ast GD}/{\rm PM}} - k_2^{\mathrm{\ast GD}/{\rm PM}}\right)\right)$, profits of the GD firm $\pi _1^{\mathrm{\ast GD}/{\rm PM}}$ decrease when g increases but remain higher than profits of the PM rival $\pi _2^{\mathrm{\ast GD}/{\rm PM}}$ that decrease at a higher rate following an increase in g. As the inequality $\pi _2^{\mathrm{\ast PM}/{\rm PM}} > \pi _2^{\mathrm{\ast PM}/{\rm GD}}$ holds for any $g < 0.37$, one gets $\pi _2^{\mathrm{\ast PM}/{\rm PM}} < \pi _2^{\mathrm{\ast PM}/{\rm GD}}$ for any $g > 0.37$. Consequently, the increased awareness toward environmental quality allows GD to become the dominant strategy of the game. This outcome, however, is Pareto inefficient for firms, as they both would jointly deviate toward PM to benefit from a reduction in the tax burden, reduce the marginal costs and obtain higher profits. Therefore, there is a conflict between self-interest and mutual benefit not to become a ‘green’-delegated firm.

5.1 The symmetric subgame SD/SD

Consider the case in which owners offer a standard output (sales) delegation contract to a manager who must choose both output and abatement levels. The utility function of the manager changes from equation (7) to take the standard form pioneered in the managerial delegation literature by Vickers (Reference Vickers1985), Sklivas (Reference Sklivas1987) and Fershtman and Judd (Reference Fershtman and Judd1987). That is:

(21)\begin{equation}{U_i} = {\pi _i} + {b_i}{q_i},\quad i = 1,2,\enspace i \ne j.\end{equation}

Equation (21) is a linear combination weighting profits and sales, where ${\pi _i}$ and ${b_i}$ are defined as in the previous section. The maximisation of the managers' utility function in equation (21) at the market stage of the game with respect to ${q_i}$ and ${k_i}$ yields the following first-order conditions:

(22)\begin{equation}\bar{q}_i^{{\rm SD/SD}} = \frac{1}{2}({1 - {q_j} - t + {b_i}} ),\;\bar{k}_i^{{\rm SD/SD}} = k_i^{{\rm SD/SD}} = t,\quad i = 1,2\ i \ne j,\end{equation}

where the superscript SD/SD stands for sales delegation of both managers. Solving the system of output reaction functions $\bar{q}_i^{{\rm SD/SD}}$ in equation (22), one gets the same solution as in equation (9), i.e., $q_i^{{\rm SD/SD}} = q_i^{{\rm GD/GD}}$. Substituting equation (9) and $k_i^{{\rm SD/SD}} = t$ into equation (1) allows us to obtain firm $i$'s profits as a function of the managerial bonuses ${b_i}$ and ${b_j}$ and the tax rate t. Comparison of the expressions in equations (2), (8) and (22) reveals that, at the pre-tax market stage of the game, the sales manager under an abatement regime is incentivised to produce the same amount and abate more than the ‘green’ manager (indeed the abated pollutant under the SD regime is the same as in the PM regime at this stage) as the former is incentivised by a contract based on sales and the latter by a contract based on emissions.

This section will also show that the design of the SD contract by the owner is such that the welfare-maximising emissions tax levied by the government at the government stage in the SD regime is set at an intermediate level between the optimal tax rate in the GD regime (the highest) and the optimal tax rate in the PM regime (the smallest). This is because production under SD is higher than under PM and abatement under SD is higher than under GD. In addition, the owner under SD will set a bonus larger than under GD as the pre-tax quantities are the same but abatement (which is not part of the contract under SD) is larger in the SD regime. This eventually implies that equilibrium production and abatement at the post-tax stage of the game under SD are the highest. The largest production under SD causes however the largest levels of aggregate emissions and environmental damage compared to the other two contracts by also implying that the SD firm will incur higher marginal costs and lower equilibrium post-tax profits than the GD firms.

Comparison amongst the crucial values obtained under SD and GD contracts (as will be clear later) implies that at the post-tax stage the working of the policy-driven mechanism – based on a transfer of resources flowing from firms to the public authority – does not allow the government to perfectly compensate the increased emissions of the SD regime as the optimal emissions tax rate is smaller than in the GD regime.

At the bonus stage, firm $i$'s owner $(i = 1,2)$ maximises profits with respect to ${b_i}$, obtaining the reaction functions in the bonus space $\bar{b}_i^{{\rm SD/SD}} = (1/4)(1 - t - {b_j}),\;i = 1,2,\;i \ne j$. Therefore, the symmetric equilibrium value of the bonus as a function of the tax rate is:

(23)\begin{equation}b_i^{{\rm SD/SD}} = \frac{1}{5}({1 - t} ),\quad i = 1,2\enspace i \ne j.\end{equation}

We first note that $b_i^{{\rm SD/SD}} > b_i^{{\rm GD/GD}}$. This is because the sales manager is incentivised to produce the same amount and abate more than the ‘green’ manager (who is incentivised by a contract based on emissions rather than sales) at the (pre-tax) market stage of the game. Further substitutions using the expression in equation (23) and other relevant equations yield the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm SD/SD}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm SD/SD}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm SD/SD}}})$ and environmental damage $({\rm E}{{\rm D}^{{\rm SD/SD}}})$ as a function of the tax rate when both firms are sales delegated under abatement (reported in online appendix B), allowing one to get social welfare under SD/SD $({\rm S}{{\rm W}^{{\rm SD/SD}}} = {\rm P}{{\rm S}^{{\rm SD/SD}}} + {\rm C}{{\rm S}^{{\rm SD/SD}}} + {\rm T}{{\rm R}^{{\rm SD/SD}}} - {\rm E}{{\rm D}^{{\rm SD/SD}}})$, which is reported in lemma 4.

Lemma 4 The social welfare function under SD/SD as a function of the tax rate is given by:

(24)\begin{equation}{\rm S}{{\rm W}^{{\rm SD}/{\rm SD}}} = \frac{{12}}{{25}} - \frac{4}{{25}}{t} - \frac{{33}}{{25}}{{t}^2} + {g}\left( { - \frac{8}{{25}} + \frac{{56}}{{25}}{t} - \frac{{98}}{{25}}{{t}^2}} \right).\end{equation}

At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 4 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm SD}/{\rm SD}}}$ and the condition under which the optimal tax rate in the subgame SD/SD is positive (see proofs of lemma 4 and proposition 4 in online appendix B).

Proposition 4 The welfare-maximising tax rate under SD/SD is given by the following expression, which is positive if and only if $g > 0.07142$:

(25)\begin{equation}{t^{\mathrm{\ast SD/SD}}} = \frac{{2({14g - 1} )}}{{98g + 33}}.\end{equation}

Using the optimal tax rate in equation (25), one obtains the equilibrium quantities of industrial production $q_i^{\mathrm{\ast SD/SD}} = ((14(2g + 1))/(98g + 33)) > 0$, executive remuneration $b_i^{\mathrm{\ast SD/SD}} = ((7(2g + 1))/(98g + 33)) > 0$, abatement $k_i^{\mathrm{\ast SD/SD}} = ((2(14g - 1))/(98g + 33)) > 0$ for any $g > 0.07142$, and emissions $q_i^{\mathrm{\ast SD/SD}} - k_i^{\mathrm{\ast SD/SD}} > 0$. Finally, inserting back the optimal tax ${t^{\mathrm{\ast SD/SD}}}$ into the profit function in equation (1), one gets equilibrium profits under SD/SD, that is:

(26)\begin{equation}\pi _i^{\mathrm{\ast SD/SD}} = \frac{{4({196{g^2} + 84g + 25} )}}{{{{(98g + 33)}^2}}}.\end{equation}

Before analysing the asymmetric subgame SD/PM and the endogenous choice at the pre-play stage between choosing to become sales delegated under pollution abatement or remaining a profit-maximising firm, it is useful to compare emissions taxes, profits, quantities, abatements, executive remunerations (bonuses), emissions and environmental damages in the symmetric subgames GD/GD, SD/SD, and PM/PM, as asymmetric Nash equilibrium outcomes are prevented in the different models of the article.

Given the results obtained in the previous sections, it is easy to see that the following sets of inequalities hold (for any $g$) at the post-tax equilibrium stage: ${t^{\ast {\rm GD/GD}}} > {t^{\mathrm{\ast SD/SD}}} > {t^{\ast {\rm PM/PM}}},\;\pi _i^{\mathrm{\ast PM/PM}} > \pi _i^{\mathrm{\ast GD/GD}} > \pi _i^{\mathrm{\ast SD/SD}}, q_i^{\mathrm{\ast SD/SD}} \,{\gt}\, q_i^{\mathrm{\ast GD/GD}} \,{=}\, q_i^{\mathrm{\ast PM/PM}}, k_i^{\mathrm{\ast SD/SD}} > k_i^{\mathrm{\ast GD/GD}} = k_i^{\mathrm{\ast PM/PM}},\ b_i^{\mathrm{\ast SD/SD}} > b_i^{\mathrm{\ast GD/GD}},\ e_i^{\mathrm{\ast SD/SD}} > e_i^{\mathrm{\ast GD/GD}} = e_i^{\mathrm{\ast PM/PM}}$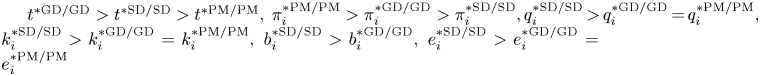 and $E{D^{\ast SD/SD}} > E{D^{\ast GD/GD}} = E{D^{\ast PM/PM}}$. This allows us to conclude that the GD contract works in the eco-friendly direction of reducing emissions and environmental damages compared to the standard SD contract under pollution abatement, while also giving firms the opportunity to generate higher profits than the strategic profile SD/SD (this is because marginal costs are higher in the SD scenario than in the GD scenario).

In addition, according to the study of the optimal bonus functions, it follows that the higher the public awareness towards environmental quality, the smaller the incentive to pollute. The relationship between ${b_i}$ and g is ‘green’ oriented, as polluting production reduces the incentive for the manager to pollute. We want to stress that we initially referred to the ‘green’-related strategic profile as ‘GD’ but do not know in advance whether the introduction of emissions instead of sales in the manager's utility is eco-friendly or anti-ecological. However, equilibrium results lie indeed within an eco-friendly trajectory.

5.2 The asymmetric subgame SD/PM

To derive the owners' endogenous choice of whether to become a sales-delegated firm or remain a profit maximiser under abatement, one must compute the outcomes of the asymmetric game in which one firm, say firm 1, is sales delegated, ${b_1} \ne 0$, and the rival, firm 2, is profit maximising, ${b_2} = 0$ (SD/PM). The two optimisation problems at the market stage of the game lead to first-order conditions as in equation (22) for SD firm 1 and as in equation (2) for PM firm 2. Solving the system of the output reaction functions, one obtains the output levels as in equation (15). Substituting these outcomes along with condition $k_1^{{\rm SD/PM}} = t$ into the profit function of the SD firm, one gets the expression of firm 1's profits as a function of the managerial incentive. It follows that firm 1's owner maximises profits with respect to ${b_1}$ at the bonus stage, leading to the optimal bonus as a function of the tax rate, that is $b_1^{{\rm SD/PM}} = (1/4)({1 - t} )$. Therefore, the subgame equilibrium outcomes as a function of the tax rate are:

(27)\begin{equation}q_1^{{\rm SD/PM}} = \frac{1}{2}({1 - t} ),\;q_2^{{\rm SD/PM}} = \frac{1}{4}({1 - t} )\quad {\rm and}\quad k_1^{{\rm SD/PM}} = k_2^{{\rm SD/PM}} = t.\end{equation}

Further substitutions by making use of equation (27) allow us to get the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm SD/PM}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm SD/PM}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm SD/PM}}})$ and environmental damage ${\rm (E}{{\rm D}^{{\rm SD/PM}}}{\rm )}$ as a function of the tax rate when firm 1 is sales delegated and firm 2 is profit maximising (reported in online appendix B), thus providing social welfare under SD/PM $({\rm S}{{\rm W}^{{\rm SD/PM}}} = {\rm P}{{\rm S}^{{\rm SD/PM}}} + {\rm C}{{\rm S}^{{\rm SD/PM}}} + {\rm T}{{\rm R}^{{\rm SD/PM}}} - {\rm E}{{\rm D}^{{\rm SD/PM}}})$, which is reported in lemma 5.

Lemma 5 The social welfare function under SD/PM as a function of the tax rate is given by:

(28)\begin{equation}{\rm S}{{\rm W}^{{\rm SD}/{\rm PM}}} = \frac{{15}}{{32}} - \frac{3}{{16}}{t} - \frac{{41}}{{32}}{{t}^2} + {g}\left( { - \frac{9}{{32}} + \frac{{33}}{{16}}{t} - \frac{{121}}{{32}}{{t}^2}} \right).\end{equation}

At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 5 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm SD}/{\rm PM}}}$ and the condition under which the optimal tax rate in the subgame SD/PM is positive (see proofs of lemma 5 and proposition 5 in online appendix B).

Proposition 5 The welfare-maximising tax rate under SD/PM is given by the following expression, which is positive if and only if $g > 0.0909$:

(29)\begin{equation}{t^{\mathrm{\ast SD/PM}}} = \frac{{3({11g - 1} )}}{{121g + 41}}.\end{equation}

Using the optimal tax rate in equation (29), one obtains the equilibrium quantities of industrial production $q_1^{\mathrm{\ast SD/PM}} = (22(2g + 1)/(121g + 41)) > 0,\;q_2^{\mathrm{\ast SD/PM}} = (11 (2g + 1)/(121g + 41)) > 0$, executive remuneration $b_1^{\mathrm{\ast SD/PM}} = (11(2g + 1)/(121g + 41)) > 0$, abatement $k_1^{\mathrm{\ast SD/PM}} = k_2^{\mathrm{\ast SD/PM}} = (3(11g - 1)/(121g + 41)) > 0$ for any $g > 0.0909$, and emissions $q_1^{\mathrm{\ast SD/PM}} - k_1^{\mathrm{\ast SD/PM}} > 0$ and $q_2^{\mathrm{\ast SD/PM}} - k_2^{\mathrm{\ast SD/PM}} > 0$ for any $0.0909 < g < 1.2727$. Finally, inserting the optimal tax ${t^{\mathrm{\ast SD/PM}}}$ back into the profit function in equation (1), one gets equilibrium profits under SD/PM for firm 1 and firm 2, respectively:

(30)\begin{equation}\pi _1^{\mathrm{\ast SD/PM}} = \frac{{3025{g^2} + 1738g + 493}}{{2{{(121g + 41)}^2}}},\;\pi _2^{\mathrm{\ast SD/PM}} = \frac{{2057{g^2} + 770g + 251}}{{2{{(121g + 41)}^2}}}.\end{equation}

5.3. The owners' endogenous choice: the sales delegation game (SD versus PM)

By using the firms' profits equations given by the expressions in equations (6), (26) and (30), one can obtain the payoff matrix reported in table 2 about the sales delegation game (SD versus PM) under abatement. The endogenous choice of firms' owners which should choose to be sales delegated (through the design of a managerial contract based on sales) or profit maximisers is played at the pre-play or contract stage of the game.

Table 2. The sales delegation game under abatement (payoff matrix): SD versus PM

To satisfy the technical restrictions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is confined to the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.125 < g < 1.2727$. The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment should be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for both PM firms in the symmetric subgame PM/PM. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment should be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the PM firm in the asymmetric subgame in which the owner of one firm designs a SD contract to its own manager and the rival is profit maximising (PM) under abatement. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.

To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2,\;i \ne j$:

(31)\begin{align}{\Delta }{\pi _a} &= \pi _i^{\mathrm{\ast SD/PM}} - \pi _i^{\mathrm{\ast PM/PM}},\;{\Delta }{\pi _b} = \pi _i^{\mathrm{\ast PM/SD}} - \pi _i^{\mathrm{\ast SD/SD}}\quad {\rm and}\notag\\ {\Delta }{\pi _c} &= \pi _i^{\mathrm{\ast PM/PM}} - \pi _i^{\mathrm{\ast SD/SD}}.\end{align}

An analytical inspection of the expressions in equation (31) reveals that ${\Delta }{\pi _a} > 0, {\Delta }{\pi _b} < 0$ and ${\Delta }{\pi _c} > 0$ for any $0.125 < g < 1.2727$, from which one can obtain the following result (see proof in online appendix B).

Result 2 resembles the standard result of Vickers (Reference Vickers1985), Fershtman and Judd (Reference Fershtman and Judd1987) and Sklivas (Reference Sklivas1987) – hereafter VFJS – in which SD is the dominant strategy but firms are entrapped in a prisoner's dilemma. This suggests that augmenting the SD game with pollution abatement does not change the main message of the SD literature framed in strategic competitive markets if products are homogeneous. In this regard, we pinpoint that considering the endogenous choice of the standard SD game without abatement (i.e., SD versus PM following the VFJS approach) leads to the well-known conclusion that the SD contract emerges as the unique pure-strategy Pareto inefficient Nash equilibrium of the game in either case of homogeneous and heterogeneous products if the manager's bonus is unilaterally chosen by the owner, though results may dramatically change if owners and managers are engaged in bargaining to choose executive remuneration (see Fanti et al., Reference Fanti, Gori and Sodini2017b), as the bargaining power interacts with the extent of product differentiation in determining the Nash equilibrium outcomes of the game. This can be very different from the classic VFJS result, according to which the SD contract without abatement is always the dominant strategy and the SD game falls under the paradigm of the prisoner's dilemma. Unlike this outcome, building on the sales delegation game (SD versus PM) under abatement can greatly modify the Nash equilibrium results of the traditional VFJS literature also in the absence of a bargaining mechanism between owners and managers over managerial contracts just by assuming horizontal product differentiation, allowing for the existence of a plethora of different Nash equilibrium outcomes depending on the interaction between the degree of product differentiation and the public awareness towards environmental quality (see online appendix C, figure A5 for details).

6.1 The asymmetric subgame GD/SD

The owners' endogenous choice about the type of delegation contract to be designed in this case needs the evaluation of the payoffs of the asymmetric game in which the owner of one firm, say firm 1, designs a delegation contract based on emissions and the rival, firm 2, designs an SD contract. The two managers' maximisation problems give the first-order conditions presented in section 4.2 for the GD firm 1 and in section 5.1 for the SD firm 2.

Solving the system of the output reaction functions at the market stage of the game, one gets the quantities of industrial production as a function of the managerial incentives as in equation (9). By substituting these outcomes along with (i) the condition $k_1^{{\rm GD/SD}} = t - {b_1}$ into the profit function of firm 1, and (ii) the condition $k_2^{{\rm GD/SD}} = t$ into the profit function of firm 2, one obtains the expressions of the firms' profits as a function of the managerial incentives. It follows that, at the bonus stage, the owner of firm 1 maximises ${\pi _1}$ with respect to ${b_1}$, and the owner of firm 2 maximises ${\pi _2}$ with respect to ${b_2}$. This generates the system of bonus reaction functions $\bar{b}_1^{{\rm GD/SD}} = (1/13)(1 - t - {b_2})$ and $\bar{b}_2^{{\rm GD/SD}} = (1/4)(1 - t - {b_1})$, whose solutions lead to the optimal bonuses as a function of the tax rate, that is, $b_1^{{\rm GD/SD}} = (1/17)(1 - t)$ and $b_2^{{\rm GD/SD}} = (1/17)(4 - t)$, so that $b_2^{{\rm GD/SD}} > b_1^{{\rm GD/SD}}$ (in line with the results of sections 4 and 5). Therefore, the equilibrium values of quantities and abatement as a function of the tax rate in this asymmetric subgame are:

(32)\begin{align}q_1^{{\rm GD/SD}} &= \frac{1}{{17}}({5 - t} ),\;q_2^{{\rm GD/SD}} = \frac{1}{{17}}({8 - t} ),\quad {\rm and}\notag\\ k_1^{{\rm GD/SD}} &= \frac{1}{{17}}({18t - 1} ),\;k_2^{{\rm GD/SD}} = t.\end{align}

From the expressions in equation (32), the inequalities $q_2^{{\rm GD/SD}} > q_1^{{\rm GD/SD}}$ and $k_2^{{\rm GD/SD}} > k_1^{{\rm GD/SD}}$ (in line with the results of sections 4 and 5). Further substitutions through the use of equation (32) allow us to get the equilibrium expressions for the producer surplus $({\rm P}{{\rm S}^{{\rm GD/SD}}})$, consumer surplus $({\rm C}{{\rm S}^{{\rm GD/SD}}})$, tax revenues $({\rm T}{{\rm R}^{{\rm GD/SD}}})$ and environmental damage $({\rm E}{{\rm D}^{{\rm GD/SD}}})$ as a function of the tax rate when firm 1 is ‘green’ delegated and firm 2 is sales delegated (reported in online appendix B), providing social welfare under GD/SD $({\rm S}{{\rm W}^{{\rm GD/SD}}} = {\rm P}{{\rm S}^{{\rm GD/SD}}} + {\rm C}{{\rm S}^{{\rm GD/SD}}} + {\rm T}{{\rm R}^{{\rm GD/SD}}} - {\rm E}{{\rm D}^{{\rm GD/SD}}})$, which is reported in lemma 6.

Lemma 6 The social welfare function under GD/SD as a function of the tax rate is given by:

(33)\begin{equation}{\rm S}{{\rm W}^{{\rm GD}/{\rm SD}}} = \frac{8}{{17}} - \frac{2}{{17}}{t} - \frac{{23}}{{17}}{{t}^2} + {g}\left( { - \frac{{98}}{{289}} + \frac{{672}}{{289}}{t} - \frac{{1152}}{{289}}{{t}^2}} \right).\end{equation}

At the first stage of the subgame, the government levies an emissions tax with the aim of maximising social welfare. Proposition 6 shows the extent of the welfare-maximising tax rate ${{t}^{{\ast} {\rm GD}/{\rm SD}}}$ and the condition under which the optimal tax rate in the subgame GD/SD is positive (see proofs of lemma 6 and proposition 6 in online appendix B).

Proposition 6 The welfare-maximising tax rate under GD/SD is given by the following expression, which is positive if and only if $g > 0.0506$:

(34)\begin{equation}{t^{\mathrm{\ast GD/SD}}} = \frac{{336g - 17}}{{1152g + 391}},\end{equation}

where ${t^{\mathrm{\ast SD/SD}}} < {t^{\mathrm{\ast GD/SD}}} < {t^{\mathrm{\ast GD/GD}}}.$

Using the optimal tax rate in equation (34), one obtains the equilibrium quantities of industrial production $q_1^{\mathrm{\ast GD/SD}} = (120(2g + 1)/ (1152g + 391)) > 0,\;q_2^{\mathrm{\ast GD/SD}} = (192(2g + 1)/ (1152g + 391)) > 0$, executive remunerations $b_1^{\mathrm{\ast GD/SD}} = (24(2g + 1)/ (1152g + 391)) > 0$ and $b_2^{\mathrm{\ast GD/SD}} = (96(2g + 1)/(1152g + 391)) > 0$, abatement $k_1^{\mathrm{\ast GD/SD}} = ((288g - 41)/(1152g + 391)) > 0$ for any $g > 0.1423,\;k_2^{\mathrm{\ast GD/SD}} = ((336g - 17)/(1152g + 391)) > 0$ for any $g > 0.0506$, and emissions $q_1^{\mathrm{\ast GD/SD}} - k_1^{\mathrm{\ast GD/SD}} > 0$ for any $0.1423 < g < 3.3541,\;q_2^{\mathrm{\ast GD/SD}} - k_2^{\mathrm{\ast GD/SD}} > 0,$. Finally, inserting the optimal tax ${t^{\mathrm{\ast GD/SD}}}$ back into the profit function in equation (1), one gets equilibrium profits under GD/SD for firm 1 and firm 2, respectively:

(35)\begin{equation}\pi _1^{\mathrm{\ast GD/SD}} = \frac{{202752{g^2} + 78432g + 22753}}{{2{{(1152g + 391)}^2}}},\;\pi _2^{\mathrm{\ast GD/SD}} = \frac{{260352{g^2} + 136032g + 37153}}{{2{{(1152g + 391)}^2}}},\end{equation}

where $\pi _2^{\mathrm{\ast GD/SD}} > \pi _1^{\mathrm{\ast GD/SD}}$.

6.2 The owners' endogenous choice: ‘green’ versus sales delegation (GD versus SD)

By using the firms' profits equations given by the expressions in equations (14), (26) and (35), one can obtain the payoff matrix reported in table 3 about the game ‘green’ versus sales delegation (GD versus SD). The endogenous choice of firms' owners, which should choose to be ‘green’ delegated or sales delegated (through the design of a managerial contract based on emissions or sales) is played at the pre-play or contract stage of the game.

Table 3. ‘Green’ delegation versus sales delegation (payoff matrix): GD versus SD

To satisfy the technical restrictions given by the feasibility constraints and obtain well-identified equilibria in pure strategies for all strategic profiles studied in the subgames presented in the previous sections, the analysis is bounded by the following range of the degree of public environmental awareness toward a clean environment (or against the damage caused by industrial production), $0.1423 < g < 3.3541$. The former inequality bounds from below the parameter region requiring that the societal awareness toward a clean environment be high enough to ensure positive levels of pollution abatement (and the optimal emissions tax rate) for the GD firm in the asymmetric subgame GD/SD. That is, when the owner of one firm designs a GD contract based on emissions to his own manager (GD) and the owner of the rival firm designs a delegation contract based on sales to his own manager (SD) under pollution abatement. The latter inequality bounds from above the parameter region requiring that the societal awareness toward a clean environment be low enough (i.e., the emissions tax rate should not be fixed at too high a level) to guarantee that emissions are non-negative for the GD firm in the asymmetric subgame. Within this range of values of g, all other relevant feasibility constraints discussed above are satisfied and apply accordingly.

To derive the Nash equilibria of the game, we study the sign of the following set of profit differentials for firm $i = 1,2,\;i \ne j$:

(36)\begin{align}{\Delta }{\pi _a} &= \pi _i^{\mathrm{\ast GD/SD}} - \pi _i^{\mathrm{\ast SD/SD}},\;{\Delta }{\pi _b} = \pi _i^{\mathrm{\ast SD/GD}} - \pi _i^{\mathrm{\ast GD/GD}}\quad {\rm and}\notag\\ {\Delta }{\pi _c} &= \pi _i^{\mathrm{\ast SD/SD}} - \pi _i^{\mathrm{\ast GD/GD}}.\end{align}

An analytical inspection of the expressions in equation (36) reveals that ${\Delta }{\pi _a} < 0, {\Delta }{\pi _b} > 0$, and ${\Delta }{\pi _c} < 0$ for any $0.1423 < g < 3.3541$, from which one can obtain Result 3 (see proof in online appendix B).

The economic intuition of the Nash equilibrium outcomes of the ‘green’ versus sales delegation game can be carried out following the narrative of the cases detailed in Result 3. Because of the strategic interactions, the design of a standard SD contract to managers arises in equilibrium regardless of the weight the government places on the environmental damage. This is because of a twofold effect: (1) on the one hand, by including emissions in the compensation scheme managers tend to behave more aggressively at the pre-tax stage of the game, expanding output, reducing abatement and eventually gaining market share more with a delegation contract based on emissions instead of sales; (2) on the other hand, however, the optimal emissions tax levied by the government is higher under GD than under SD as managers tend to produce and pollute more if owners design a contract based on emissions instead of sales. The latter effect more than counterbalances the former so that the post-tax profits are larger in the symmetric GD scenario than in the symmetric SD scenario (irrespective of the value of $^g$).

In addition, as in the asymmetric scenario, the SD firm gets higher profits than the GD firm: SD is the dominant strategy of this game. We note that managers under SD abate more pollution than under GD and pay a lower amount of taxes. However, the SD manager produces more than the GD manager so that marginal costs under GD are smaller than under SD and the tax base tends to decrease in the latter case. Owners therefore will improve firms' profitability if they jointly deviate towards GD; in fact, by reducing output (and thus emissions), profits will increase, and as the percentage reduction in output gets lower, the percentage increases in the market price get higher. Therefore, by choosing the standard SD contract, owners are cast into a prisoner's dilemma and this result is policy-driven in the sense that emissions taxation is higher in the GD scenario than in the SD scenario due to the relative size of production and abatement in the two regimes.

We pinpoint here that, by changing the structure of the three games studied in sections 4–6 and considering the setting of the emissions fee occurring at the first stage (i.e., the regulator moves first), we avoid including the pre-play stage, which confirms the Nash equilibrium outcomes of the article except for the GD game, in which only (GD,GD) emerges as the unique Pareto-inefficient Nash equilibrium.