1. Introduction
The theme of environmental protection is one of the most important priorities on the agenda for policy makers and governments across the globe. In particular, the discussion has focused on which policy instrument should be adopted to induce firms to reduce the level of pollution emissions. The conventional instrument, a tax proportional to the level of pollution, has often been criticized, on the grounds that it is very difficult to measure the exact damage produced by each firm. Alternative tools have been proposed and policies have been suggested.
Many commentators argue that educating citizens/consumers to respect the environment may prove to be a very effective instrument, as it rewards green producers to the detriment of polluting brown ones. Turaga et al. (Reference Turaga, Howarth and Borsuk2010: 211) claim that ‘inducing pro-environmental behaviors in individuals, is one of the most important challenges in the path to sustainability’. However, shaping an environmental culture requires a long-term investment, as it involves teaching environmental values at school, organizing outdoor initiatives that instill respect for nature, and providing infrastructures and services in support of renewable energy and recycling. A short-term alternative often adopted by governments is to introduce environmental awareness campaigns.Footnote 1 Indeed, there is recent evidence of public authorities launching campaigns to warn citizens about the harmful effects of bad consumption habits on the environment. This is particularly common in the automotive sector. The Italian guidelines on CO2 emission savings rank vehicles according to their environmental impact.Footnote 2 In the United States, the EPA SmartWay program compares the environmental performance of vehicles.Footnote 3 The Green Vehicle Guide promoted by the Australian government helps drivers by rating circulating vehicles on the basis of greenhouse and air pollution emissions.Footnote 4
How do consumers react to such initiatives? Are they really willing to switch to a green good, even if the pure satisfaction deriving from its consumption is lower than that of a brown good? Electric vehicles (EVs), for example, have yet to reach a level of performance and comfort comparable to that of traditional internal combustion engine vehicles (ICEVs).Footnote 5 Depending on whether consumers value the pure performance of the product more (or less!) than its environmental impact, the same policy tool may affect consumers’ choice differently. This is what we want to capture in our paper. To this aim, we compare traditional policy instruments such as imposing taxes on polluting firms with recently established initiatives such as environmental awareness campaigns that inform consumers about the relative environmental impact of the goods they purchase.
We adopt a model of vertical differentiation where two firms compete in prices. As usual, they differentiate their products by quality as a way to mitigate competition and increase profits (Gabszewicz and Thisse, Reference Gabszewicz and Thisse1979; Shaked and Sutton, Reference Shaked and Sutton1982). In particular, one of the two firms produces the green good and pays an additional cost for it, while the other firm produces a polluting good, and may be subject to environmental taxation.
Based on our preliminary discussion, we consider two different scenarios, depending on whether consumers’ aprioristic preferences are such that they either value the environmental quality of the goods (their polluting emissions) or their hedonic quality (their pure performance).Footnote 6 In the first case, following most of the literature (e.g., Moraga-Gonzalez and Padron-Fumero, Reference Moraga-Gonzalez and Padron-Fumero2002; Lombardini-Riipinen, Reference Lombardini-Riipinen2005; Deltas et al., Reference Deltas, Harrington and Khanna2013; Ben Elhadj and Tarola, Reference Ben Elhadj and Tarola2015), we assume that the green good is of high quality and the polluting brown good is of low quality. In the second case, based on the observation that quite often brown goods have higher performance than green alternatives (e.g., Weatherell et al., Reference Weatherell, Tregear and Allinson2003; Gupta and Ogden, Reference Gupta and Ogden2009; Mantovani et al., Reference Mantovani, Tarola and Vergari2016), we assume that the high-quality good is the one that pollutes whereas the low-quality good is green.
In each scenario, we build a two-stage game in which the government intervenes in the first stage either by taxing the polluting firm, or by indirectly rewarding the green firm through an environmental campaign. In the second stage, firms compete in prices. A crucial point of our model is that the campaign is designed to raise consumers’ awareness about the impact of their consumption choices on the ecosystem in which they live. In particular, by comparing the environmental impact of the two products, its aim is to persuade consumers to attach an extra positive value to the green good while at the same time stigmatizing the consumption of the brown one. This is captured by resorting to the theory of relative preferences, initially developed by Ghazzai (Reference Ghazzai2008) as well as Alexopoulos and Sapp (Reference Alexopoulos and Sapp2006), and recently reconsidered by Ben Elhadj and Tarola (Reference Ben Elhadj and Tarola2015).
Our main results are as follows. When consumers initially value the environmental quality, so that they all agree that the green good has a higher quality than the brown good, the awareness campaign can be socially more efficient than the pollution tax. This happens when the cost of the campaign is not excessive, and when the green expansion effect is sufficiently high. Such an effect is related to the increase in the demand for the green good resulting from the campaign, achieved at the expense of the brown (low-quality) good, and proportional to the average willingness to pay for the environmental quality.
On the contrary, when consumers initially value the hedonic quality of a product (which may be at odds with their environmental quality), then taxation always prevails in terms of social welfare. In such a scenario the campaign is relatively costly and limited in scope; even though its message has been incorporated, consumers do not value the environmental component enough to outweigh their innate inclination towards the hedonic quality. Nonetheless, the campaign may be preferred if the policy maker is particularly interested in consumer surplus. Indeed, in the case of hedonic qualities, the green expansion effect does not only consist of stealing market shares from the brown (high-quality) producer, but it also expands market coverage, thus increasing total output. This may contribute to resolving the frequently observed conflict between environmental and competition policy, as the campaign is capable of reconciling output provision with pollution reduction.
The main message of our contribution can therefore be summarized as follows. Based on total surplus as a measure of social welfare, an environmental campaign activating relative preferences is less efficient than a traditional taxation instrument when consumers are mainly interested in the pure performance of a product. The result may change with green consumerism, in which case the campaign can achieve a higher total surplus than taxation. Our analysis can thus provide valuable environmental policy indications, depending on region-specific consumer preferences and socio-economic conditions.
Looking at the empirical evidence, aprioristic environmental preferences vary across countries as well as over time due to socio-economic conditions. Bhate (Reference Bhate2001) and Hopkins and Mehanna (Reference Hopkins and Mehanna2000), inter alia, show that consumers in developing countries are at the early stage of green consumerism, thus ranking economic interests before environmental concerns. Greenstone and Jack (Reference Greenstone and Jack2015: 7) point out that, although developing countries face higher health burdens than developed countries due to poorer environmental conditions, ‘the small handful of studies measuring marginal willingness to pay (MWTP) for environmental quality improvements indicate low valuations by affected households’. One of the main explanations provided by the authors is due to low income. Hence, in countries characterized by limited environmental concern (low MWTP for environmental quality), an indirect policy instrument like a campaign is less likely to efficiently fight pollution. As for developed countries, a European survey conducted between April and May 2011 on citizens’ attitude towards the environment (Special Eurobarometer 365) showed that most EU citizens feel that environmental issues have a direct impact on their everyday lives and they are also inclined to play a proactive role in protecting the environment.Footnote 7 According to our model, in such countries the type of campaign that we have in mind may perform better than the tax instrument from the social perspective. As a case in point, the recent informative campaigns in the automotive sector that we introduced before have been launched in developed countries.
Our paper contributes to identifying which policy tool is more efficient in reducing polluting emissions in the presence of environmentally concerned consumers. The papers by Moraga-Gonzalez and Padron-Fumero (Reference Moraga-Gonzalez and Padron-Fumero2002) and Lombardini-Riipinen (Reference Lombardini-Riipinen2005) are useful references. In the former, the authors compare some frequently used environmental policies: emissions standard, ad valorem tax and technology subsidization. They demonstrate that aggregate emissions may increase as a result of government regulation due to the strategic responses of the firms to those regulations. In the latter, Lombardini-Riipinen (Reference Lombardini-Riipinen2005) finds that the first-best level of quality can be obtained by combining a uniform ad valorem tax with an emission tax (or a subsidy to consumers buying green products). In a recent book, Lambertini (Reference Lambertini2013: ch. 6) provides a careful discussion about the possibility that environmentally aware consumers may regulate firms’ behavior even in the absence of an explicit policy measure. We complement this stream of research by explicitly considering a policy intervention such as a campaign which makes consumers aware of the relative environmental impact of the products.
The idea of an environmental campaign as an alternative policy instrument has been recently analyzed in other contributions. Sartzetakis et al. (Reference Sartzetakis, Xepapadeas and Petrakis2012) study, in a dynamic framework, the role of information provision on environmental damages associated with the consumption of certain products as a policy instrument that supplements environmental taxation. In their model, the campaign takes the form of costly informative advertising and it helps to reduce the asymmetry of information between consumers and manufacturers. Van der Made and Schoonbeek (Reference van der Made and Schoonbeek2009) consider a campaign that increases consumers’ environmental concern through persuasive advertising. Kaufman (Reference Kaufman2014) develops a dynamic model of observational learning and costly search to investigate whether financial incentives or informational campaigns are more effective at encouraging green purchasing. These contributions thus support the environmental campaign as a policy instrument to supplement and/or substitute for other traditional environmental policies.
In our paper, the campaign induces consumers to include an additional component in their overall valuation of quality which is captured through the key concept of relative preferences. In this perspective, our framework is somewhat similar to that of Ben Elhadj and Tarola (Reference Ben Elhadj and Tarola2015). They investigate how quality competition is affected by relative preferences. They find that the presence of such preferences may contribute to reducing pollution damage by inducing the polluting firm to increase its environmental quality. They also introduce the possibility of country-specific preferences, thus providing: (i) theoretical foundation to the empirical evidence that green consumerism changes with socio-economic conditions; and (ii) initial suggestions for the use of new environmental policy tools. Notice, however, that they focus on relative preferences for environmental quality. We complement their analysis in two ways. First, we make explicit the proactive role of environmental campaigns in activating relative preferences and compare them with taxation. Secondly, we also analyze the role played by this additional component of preferences in a scenario where consumers initially value only the pure performance of a product rather than its environmental impact/quality.Footnote 8
The rest of the paper is organized as follows. Section 2 presents the case of environmental qualities, while section 3 deals with hedonic qualities. Section 4 summarizes our main results. Section 5 discusses the assumptions of our model and provides some formal extensions to confirm the robustness of our results. Section 6 concludes.
2. Environmental qualities
Consider two goods of different environmental quality: good H produced by firm H is green, while good L produced by firm L is brown. We are in line with most of the literature as we assume that consumers value the environmental quality of a product: they all agree that good H has a higher quality than good L. There is a continuum of consumers indexed by θ which is uniformly distributed in the interval [0, Θ]. Thus, θ measures consumers’ valuation of environmental quality, while Θ>0 indicates consumers’ heterogeneity as well as the average valuation of the environmental quality in the market.
As for the cost specification, we assume that producing the green good requires a constant marginal cost, c>0, whereas the brown quality is produced at zero cost. The additional cost c can be conceived of either in terms of a more costly technology or of the cleaning activity carried out by the green producer. Pollution creates an environmental damage D which is proportional to the emissions released by the brown firm: D=e·x L , where x L is the quantity produced by the polluting firm. The green good is assumed to be emission free. Parameter e>0 captures the marginal social cost of pollution.
We develop the following two-stage game. First, the policy maker decides which policy instrument to use in order to reduce the environmental damage for any given level of per-unit emissions. Then, firms compete in prices. We solve the game by backward induction: we start by solving the price competition stage for the two cases (campaign and taxation), and then we carry out the proper comparison to find out the policy maker's decision.
2.1. Supporting the environmental campaign
We first consider the environmental campaign. Our modelling strategy draws insights from social psychology and in particular from the Norm-Activation Theory (Schwartz, Reference Schwartz1970, Reference Schwartz1977), one of the most widely accepted and empirically supported theories of moral motivation. According to this theory, the activation of personally held moral norms influences pro-environmental behavior. As extensively reviewed by Turaga et al. (Reference Turaga, Howarth and Borsuk2010: 212), the activation of personal norms is based on two preconditions: ‘the individual must be aware that her action has consequences for the welfare of others [...] and the individual must feel a personal responsibility to undertake that action.’ Formally, we assume that the policy maker can activate these personal moral norms to pro-environmental behavior by engaging in a costly awareness campaign. In particular, the campaign is capable of creating a bad conscience for brown consumers while at the same time rewarding green consumers for taking eco-friendly actions.Footnote 9 Accordingly, a consumer of type θ∈[0, Θ] has the following utility:
 $$U(\theta) = \left\{\matrix{\theta q_{H} - p_{H} + \gamma (q_{H} - q_{L}) &\hbox{if she buys the green good}, \hfill \cr \theta q_{L} - p_{L} - \gamma (q_{H} - q_{L}) \hfill &\hbox{if she buys the brown good}, \hfill \cr 0 \hfill &\hbox{if she refrains from buying}, \hfill} \right.$$
$$U(\theta) = \left\{\matrix{\theta q_{H} - p_{H} + \gamma (q_{H} - q_{L}) &\hbox{if she buys the green good}, \hfill \cr \theta q_{L} - p_{L} - \gamma (q_{H} - q_{L}) \hfill &\hbox{if she buys the brown good}, \hfill \cr 0 \hfill &\hbox{if she refrains from buying}, \hfill} \right.$$
where q H >q L indicates the environmental qualities of the two goods, whose prices are respectively indicated with p H and p L .
The above representation does not directly include pollution. However, compared to the standard model of vertical differentiation (Gabszewicz and Thisse, Reference Gabszewicz and Thisse1979), the utility from buying good i={H, L} is modified by introducing the term γ (q i −q j ) with i≠j. It follows that the satisfaction deriving from a product variant can be either amplified or decreased by the environmental characteristics of i as compared to j. The intensity of such relative preferences is measured by γ≥0. The stronger the policy maker's support for the campaign, the higher the value of γ, and thus the higher the impact of the moral component of consumption. On the contrary, when γ→0 we revert to the standard vertical differentiation model. In other words, the campaign represents an indirect approach to fighting pollution emissions by encouraging consumers to increase the consumption of the green good, thus generating a green expansion effect.Footnote 10
The consumer indifferent between buying the low-quality good and not buying at all is:
while the consumer indifferent between buying the low- and the high-quality good is:
The demands for the two goods are formally written as:
![]() $x_{L} = \theta_{H} - \theta_{L}$
and
$x_{L} = \theta_{H} - \theta_{L}$
and
![]() $x_{H} = \Theta - \theta_{H}$
.Footnote
11
Compared to the traditional setting (γ=0), here at given prices the market share of H increases in γ at the expense of that of L, as θ
H
shifts leftward, while θ
L
shifts rightward. The green expansion effect consists of a pure stealing effect, as some consumers switch from the brown to the green good. As we assumed that a constant marginal cost c>0 only applies to the production of the green good, profits are given by
$x_{H} = \Theta - \theta_{H}$
.Footnote
11
Compared to the traditional setting (γ=0), here at given prices the market share of H increases in γ at the expense of that of L, as θ
H
shifts leftward, while θ
L
shifts rightward. The green expansion effect consists of a pure stealing effect, as some consumers switch from the brown to the green good. As we assumed that a constant marginal cost c>0 only applies to the production of the green good, profits are given by
![]() $\pi _{H}=x_{H}(p_{H}-c)$
and
$\pi _{H}=x_{H}(p_{H}-c)$
and
![]() $\pi_{L}=p_{L}x_{L}$
. Additional conditions on c and γ will be specified below.
$\pi_{L}=p_{L}x_{L}$
. Additional conditions on c and γ will be specified below.
Proceeding by backward induction, we solve the price competition stage and derive the main results, which are valid for any quality configuration. Using First Order Conditions (FOCs)\reversemarginpar equilibrium prices as a function of qualities are:
 $$\eqalign{p_{L}^{\ast E} &= {q_{L}[c + \Theta (q_{H} - q_{L})] - 2\gamma q_{H} (q_{H} - q_{L}) \over 4q_{H}-q_{L}}, \cr p_{H}^{\ast E} &= {2cq_{H} + (q_{H} - q_{L}) [2 \Theta q_{H} + \gamma (3q_{H} - q_{L})] \over 4q_{H} - q_{L}},}$$
$$\eqalign{p_{L}^{\ast E} &= {q_{L}[c + \Theta (q_{H} - q_{L})] - 2\gamma q_{H} (q_{H} - q_{L}) \over 4q_{H}-q_{L}}, \cr p_{H}^{\ast E} &= {2cq_{H} + (q_{H} - q_{L}) [2 \Theta q_{H} + \gamma (3q_{H} - q_{L})] \over 4q_{H} - q_{L}},}$$
where additional superscript E indicates that we are considering environmental qualities.Footnote
12
Both demands are positive if
![]() $p_{H}^{\ast E} \gt p_{L}^{\ast E}$
. If instead
$p_{H}^{\ast E} \gt p_{L}^{\ast E}$
. If instead
![]() $p_{H}^{\ast E} \leq p_{L}^{\ast E}$
, then the demand for the low-quality good would be zero (x
L
=0) while that for the high-quality good would be
$p_{H}^{\ast E} \leq p_{L}^{\ast E}$
, then the demand for the low-quality good would be zero (x
L
=0) while that for the high-quality good would be
![]() $x_{H} = \Theta - {p_{L}+\gamma (q_{H}-q_{L}) \over q_{L}}$
. We consider the case in which both firms are active in the market. This requires the conditions provided in the following lemma to hold. Define:
$x_{H} = \Theta - {p_{L}+\gamma (q_{H}-q_{L}) \over q_{L}}$
. We consider the case in which both firms are active in the market. This requires the conditions provided in the following lemma to hold. Define:
Lemma 1
The market is uncovered and both firms are active iff
![]() $\Theta \gt \underline{\Theta }^{E}$
and
$\Theta \gt \underline{\Theta }^{E}$
and
![]() $\gamma \lt \overline{\gamma}^{E}$
.
$\gamma \lt \overline{\gamma}^{E}$
.
Proof: See the appendix. □
We assume that the conditions reported in Lemma 1 hold throughout the paper. They indicate that a sufficiently large consumer heterogeneity together with a non-excessive level of the moral component of consumption activated by the campaign are required for both firms to coexist in the market. We limit our attention to such a case as we want to reproduce a concrete situation where polluting firms compete in the market with non-polluting ones. Equilibrium demands/outputs are:
 $$\eqalign{x_{L}^{\ast E} &= {q_{H}\{q_{L}[c+\Theta (q_{H}-q_{L})]-2\gamma q_{H}(q_{H}-q_{L}) \} \over (q_{H}-q_{L})(4q_{H}-q_{L}) q_{L}}, \cr x_{H}^{\ast E} &= {[\gamma (3q_{H}-q_{L}) +2\Theta q_{H}](q_{H}-q_{L}) -c(2q_{H}-q_{L}) \over (q_{H}-q_{L}) (4q_{H}-q_{L})}.}$$
$$\eqalign{x_{L}^{\ast E} &= {q_{H}\{q_{L}[c+\Theta (q_{H}-q_{L})]-2\gamma q_{H}(q_{H}-q_{L}) \} \over (q_{H}-q_{L})(4q_{H}-q_{L}) q_{L}}, \cr x_{H}^{\ast E} &= {[\gamma (3q_{H}-q_{L}) +2\Theta q_{H}](q_{H}-q_{L}) -c(2q_{H}-q_{L}) \over (q_{H}-q_{L}) (4q_{H}-q_{L})}.}$$
Notice that
![]() $x_{L}^{\ast E}$
decreases with γ, while
$x_{L}^{\ast E}$
decreases with γ, while
![]() $x_{H}^{\ast E}$
increases with γ. However,
$x_{H}^{\ast E}$
increases with γ. However,
![]() $\partial (x_{H}^{\ast E} + x_{L}^{\ast E})/\partial \gamma \lt 0$
: total output diminishes with γ, as expected. This reveals that, in the case of environmental qualities, the campaign gives rise to the classical tradeoff between output provision and pollution abatement that often characterizes the complex relationship between environmental and competition policies. We will come back to this point when considering hedonic qualities. Equilibrium profits are given by:
$\partial (x_{H}^{\ast E} + x_{L}^{\ast E})/\partial \gamma \lt 0$
: total output diminishes with γ, as expected. This reveals that, in the case of environmental qualities, the campaign gives rise to the classical tradeoff between output provision and pollution abatement that often characterizes the complex relationship between environmental and competition policies. We will come back to this point when considering hedonic qualities. Equilibrium profits are given by:
The social welfare as a function of γ is written in a compact way as:
where
![]() $e\cdot x_{L}^{\ast E}$
is the environmental damage, while
$e\cdot x_{L}^{\ast E}$
is the environmental damage, while
![]() $s {\gamma^{2} \over 2}$
is the cost for the campaign, which is assumed to be convex in γ.Footnote
13
This captures the idea that it is increasingly costly for the policy maker to affect consumers’ preferences through the comparative information provided by the campaign.Footnote
14
Parameter s>0 is inversely related to the effectiveness of the campaign effort. The social welfare is concave in γ only for sufficiently high values of s. In particular, this requires:
$s {\gamma^{2} \over 2}$
is the cost for the campaign, which is assumed to be convex in γ.Footnote
13
This captures the idea that it is increasingly costly for the policy maker to affect consumers’ preferences through the comparative information provided by the campaign.Footnote
14
Parameter s>0 is inversely related to the effectiveness of the campaign effort. The social welfare is concave in γ only for sufficiently high values of s. In particular, this requires:
We assume that
![]() $s \gt \underline{s}$
and compute the optimal level of γ that maximizes social welfare:Footnote
15
$s \gt \underline{s}$
and compute the optimal level of γ that maximizes social welfare:Footnote
15
 $$\gamma^{\ast E}= {\matrix{2eq_{H}^{2}(4q_{H}-q_{L}) +q_{L}[2c(6q_{H}q_{L}-10q_{H}^{2}-q_{L}^{2})\cr[3pt] +\,\Theta q_{H}(8q_{H}-3q_{L}) (q_{H}-q_{L}) ]} \over sq_{L}(4q_{H}-q_{L})^{2}-(q_{H}-q_{L}) (12q_{H}^{3}+2q_{L}^{3}-13q_{H}q_{L}^{2}+19q_{H}^{2}q_{L})}.$$
$$\gamma^{\ast E}= {\matrix{2eq_{H}^{2}(4q_{H}-q_{L}) +q_{L}[2c(6q_{H}q_{L}-10q_{H}^{2}-q_{L}^{2})\cr[3pt] +\,\Theta q_{H}(8q_{H}-3q_{L}) (q_{H}-q_{L}) ]} \over sq_{L}(4q_{H}-q_{L})^{2}-(q_{H}-q_{L}) (12q_{H}^{3}+2q_{L}^{3}-13q_{H}q_{L}^{2}+19q_{H}^{2}q_{L})}.$$
Taking into account that
![]() $\gamma ^{\ast E}$
has to be non-negative and that the conditions reported in Lemma 1 have to be satisfied, we find:
$\gamma ^{\ast E}$
has to be non-negative and that the conditions reported in Lemma 1 have to be satisfied, we find:
Lemma 2
![]() $\gamma ^{\ast E}\in \lbrack 0,\overline{\gamma }^{E})$
when
$\gamma ^{\ast E}\in \lbrack 0,\overline{\gamma }^{E})$
when
![]() $e \in \lbrack \max \{0,\underline{e}^{\gamma E}\},\overline{e}^{\gamma E})$
.
$e \in \lbrack \max \{0,\underline{e}^{\gamma E}\},\overline{e}^{\gamma E})$
.
Proof: See the appendix, which also provides the precise values of
![]() $\underline{e}^{\gamma E}$
and
$\underline{e}^{\gamma E}$
and
![]() $\overline{e}^{\gamma E}$
. □
$\overline{e}^{\gamma E}$
. □
Hence, the optimal policy is γ=0 as long as the emission level is very low, since the positive effect resulting from the emission reduction does not compensate for the cost of the campaign. In contrast, for very high values of the emission, the policy maker sets
![]() $\gamma =\overline{\gamma }^{E}$
, the expression of which is reported in (2). Only for intermediate levels of e is the optimal policy given by
$\gamma =\overline{\gamma }^{E}$
, the expression of which is reported in (2). Only for intermediate levels of e is the optimal policy given by
![]() $\gamma =\gamma ^{\ast E}$
. The previous discussion is summarized into:
$\gamma =\gamma ^{\ast E}$
. The previous discussion is summarized into:
Remark 1
The government optimally sets: (i) γ=0 when
![]() $e \lt \max \{0,\underline{e}^{\gamma E}\}$
; (ii)
$e \lt \max \{0,\underline{e}^{\gamma E}\}$
; (ii)
![]() $\gamma =\gamma^{\ast E}$
when
$\gamma =\gamma^{\ast E}$
when
![]() $e\in \lbrack \max \{0,\underline{e}^{\gamma E}\},\overline{e}^{\gamma E})$
; (iii)
$e\in \lbrack \max \{0,\underline{e}^{\gamma E}\},\overline{e}^{\gamma E})$
; (iii)
![]() $\gamma = \overline{\gamma }^{E}$
when
$\gamma = \overline{\gamma }^{E}$
when
![]() $e \geq \overline{e}^{\gamma E}$
.
$e \geq \overline{e}^{\gamma E}$
.
2.2. Taxing the polluting good
Let us now consider the traditional taxation instrument. According to social psychology (e.g., Frey, Reference Frey1997; Turaga et al., Reference Turaga, Howarth and Borsuk2010) as well as being widely discussed in the public economic literature (e.g., Brekke et al., Reference Brekke, Kverndokk and Nyborg2003; Nyborg et al., Reference Nyborg, Howarth and Brekke2006), when the government adopts a direct taxation policy to reduce pollution, the influence of moral motivation can decrease.Footnote
16
Accordingly, we assume that when the policy maker decides to levy a tax proportional to the polluting emission on the brown firm, then the pro-environmental component of consumption is not relevant, i.e.,
![]() $\gamma \rightarrow 0$
.Footnote
17
Formally, inserting γ=0 in (1) is equivalent to considering a standard vertical differentiation model, where
$\gamma \rightarrow 0$
.Footnote
17
Formally, inserting γ=0 in (1) is equivalent to considering a standard vertical differentiation model, where
![]() $\theta_{L} = p_{L}/q_{L}$
is the consumer indifferent between buying the low-quality good and not buying at all, while
$\theta_{L} = p_{L}/q_{L}$
is the consumer indifferent between buying the low-quality good and not buying at all, while
![]() $\theta _{H} = (p_{H} - p_{L})/q_{H} - q_{L}$
is the consumer indifferent between buying the low- and the high-quality good. Demands are given by
$\theta _{H} = (p_{H} - p_{L})/q_{H} - q_{L}$
is the consumer indifferent between buying the low- and the high-quality good. Demands are given by
![]() $x_{L} = \theta_{H} - \theta_{L}$
and
$x_{L} = \theta_{H} - \theta_{L}$
and
![]() $x_{H} = \Theta - \theta_{H}$
.
$x_{H} = \Theta - \theta_{H}$
.
The green good is produced at cost c, whereas the polluting good is subject to a per-unit tax t. Thus, t can be interpreted as the tax differential between the two firms, while c represents the marginal production cost differential. Profit functions are therefore
![]() $\pi_{L} = (p_{L} - t) x_{L}$
and
$\pi_{L} = (p_{L} - t) x_{L}$
and
![]() $\pi_{H} = (p_{H} - c) x_{H}$
. Price competition yields:
$\pi_{H} = (p_{H} - c) x_{H}$
. Price competition yields:
 $$\eqalign{p_{H}^{\ast \ast E} &= {q_{H}[2c + t + 2\Theta (q_{H} - q_{L})] \over 4q_{H} - q_{L}} \gt 0, \cr p_{L}^{\ast \ast E} &= {cq_{L} + 2tq_{H} + q_{L} \Theta (q_{H} - q_{L}) \over 4q_{H} - q_{L}} \gt 0.}$$
$$\eqalign{p_{H}^{\ast \ast E} &= {q_{H}[2c + t + 2\Theta (q_{H} - q_{L})] \over 4q_{H} - q_{L}} \gt 0, \cr p_{L}^{\ast \ast E} &= {cq_{L} + 2tq_{H} + q_{L} \Theta (q_{H} - q_{L}) \over 4q_{H} - q_{L}} \gt 0.}$$
Let us now define:
Lemma 3
Both firms stay in the market iff
![]() $\Theta > \underline{\Theta }^{E}$
and
$\Theta > \underline{\Theta }^{E}$
and
![]() $t<\overline{t}^{E}$
.
$t<\overline{t}^{E}$
.
Proof: See the appendix, and recall that
![]() $\underline{\Theta}^{E}$
is defined in (2). □
$\underline{\Theta}^{E}$
is defined in (2). □
We assume that the conditions reported in Lemma 3 hold throughout the paper. They indicate that a sufficiently large consumer heterogeneity together with a non-excessive taxation are required for both firms to coexist in the market. Equilibrium demands are:
 $$\eqalign{x_{L}^{\ast \ast E} &= {q_{H}\lsqb cq_{L}-t\lpar 2q_{H}-q_{L}\rpar +\Theta q_{L}(q_{H}-q_{L})\rsqb \over (q_{H}-q_{L}) \lpar 4q_{H}-q_{L}\rpar q_{L}}, \cr x_{H}^{\ast \ast E} &= {2\Theta q_{H}(q_{H}-q_{L})-c(2q_{H}-q_{L})+tq_{H} \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L})}.}$$
$$\eqalign{x_{L}^{\ast \ast E} &= {q_{H}\lsqb cq_{L}-t\lpar 2q_{H}-q_{L}\rpar +\Theta q_{L}(q_{H}-q_{L})\rsqb \over (q_{H}-q_{L}) \lpar 4q_{H}-q_{L}\rpar q_{L}}, \cr x_{H}^{\ast \ast E} &= {2\Theta q_{H}(q_{H}-q_{L})-c(2q_{H}-q_{L})+tq_{H} \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L})}.}$$
Notice that
![]() $\partial x_{L}^{\ast \ast E}/\partial t \lt 0$
and
$\partial x_{L}^{\ast \ast E}/\partial t \lt 0$
and
![]() $\partial x_{H}^{\ast \ast E}/\partial t \gt 0$
, as expected. Moreover,
$\partial x_{H}^{\ast \ast E}/\partial t \gt 0$
, as expected. Moreover,
![]() $\partial (x_{H}^{\ast \ast E} + x_{L}^{\ast \ast E})/\partial t \lt 0$
: total output decreases with t, and consumer surplus is therefore negatively affected by environmental taxation. Equilibrium profits are given by:
$\partial (x_{H}^{\ast \ast E} + x_{L}^{\ast \ast E})/\partial t \lt 0$
: total output decreases with t, and consumer surplus is therefore negatively affected by environmental taxation. Equilibrium profits are given by:
Social welfare as a function of t can be written in a compact form as:
Algebraic calculations show that it is concave in t. The optimal tax rate is:
Taking into account that t* E has to be non-negative, and that the conditions from Lemma 3 have to be satisfied, we demonstrate that:
Lemma 4
![]() $t^{\ast E}\in \lbrack 0,\overline{t}^{E})$
when
$t^{\ast E}\in \lbrack 0,\overline{t}^{E})$
when
![]() $e\in \lbrack \max \lcub 0, \underline{e}^{tE} \rcub , \overline{e}^{tE})$
.
$e\in \lbrack \max \lcub 0, \underline{e}^{tE} \rcub , \overline{e}^{tE})$
.
Proof: See the appendix, which also reports the precise values of
![]() $\underline{e}^{tE}$
and
$\underline{e}^{tE}$
and
![]() $\overline{e}^{tE}$
. □
$\overline{e}^{tE}$
. □
For low values of e, the optimal tax is set to zero because the negative effect on output is in absolute value stronger than the positive effect obtained by reducing pollution emissions. On the contrary, for high values of e, the optimal tax is
![]() $\overline{t}^{E}$
– whose value is expressed in (5) – and the profit of the low brown quality firm tends to zero. However, it is relatively easy to demonstrate that the government would prefer to leave an
$\overline{t}^{E}$
– whose value is expressed in (5) – and the profit of the low brown quality firm tends to zero. However, it is relatively easy to demonstrate that the government would prefer to leave an
![]() $\varepsilon \rightarrow 0$
to the polluting firm, and then still have a duopoly, instead of pushing it off the market. We summarize the optimal tax policy in the following remark:
$\varepsilon \rightarrow 0$
to the polluting firm, and then still have a duopoly, instead of pushing it off the market. We summarize the optimal tax policy in the following remark:
Remark 2
The government optimally sets: (i) t=0 when
![]() $e<\max \lcub 0,\underline{e}^{tE}\rcub $
; (ii) t=t*
E
when
$e<\max \lcub 0,\underline{e}^{tE}\rcub $
; (ii) t=t*
E
when
![]() $e\in \lbrack \max \lcub 0,\underline{e}^{tE}\rcub ,\overline{e}^{tE});$
(iii)
$e\in \lbrack \max \lcub 0,\underline{e}^{tE}\rcub ,\overline{e}^{tE});$
(iii)
![]() $t=\overline{t}^{E}$
when
$t=\overline{t}^{E}$
when
![]() $e\geq \overline{e}^{tE}$
.
$e\geq \overline{e}^{tE}$
.
Remark 2 confirms that the optimal tax rate is non-decreasing in the intensity of polluting emissions captured by parameter e.
2.3. Comparing the two instruments under environmental qualities
We compare the social efficiency of taxation vs. campaign to find out which policy instrument should be adopted by the policy maker. First of all, we need to rank the threshold values of e that define the regions where different levels of social welfare occur. In the appendix we detail all the possible cases and evaluate the relative comparisons. The following proposition summarizes the most important results. Let
 $$\eqalign{\Theta_{1}&= {2c(28q_{H}^{4}-53q_{H}^{3}q_{L}+36q_{H}^{2} q_{L}^{2}-10q_{H}q_{L}^{3}+q_{L}^{4}) \over q_{H}\lpar 4q_{H}-3q_{L}\rpar (q_{H}-q_{L}) (10q_{H}^{2}-6q_{H}q_{L}+q_{L}^{2})},\cr \Theta _{2}&= {2c\lpar 2q_{H}-q_{L}\rpar ^{2} \over q_{H}\lpar 4q_{H}^{2}-7q_{H}q_{L}+3q_{L}^{2}\rpar}, \hbox{with}\,\Theta_{1} \lt \Theta_{2}.}$$
$$\eqalign{\Theta_{1}&= {2c(28q_{H}^{4}-53q_{H}^{3}q_{L}+36q_{H}^{2} q_{L}^{2}-10q_{H}q_{L}^{3}+q_{L}^{4}) \over q_{H}\lpar 4q_{H}-3q_{L}\rpar (q_{H}-q_{L}) (10q_{H}^{2}-6q_{H}q_{L}+q_{L}^{2})},\cr \Theta _{2}&= {2c\lpar 2q_{H}-q_{L}\rpar ^{2} \over q_{H}\lpar 4q_{H}^{2}-7q_{H}q_{L}+3q_{L}^{2}\rpar}, \hbox{with}\,\Theta_{1} \lt \Theta_{2}.}$$
Proposition 1
Assume that consumers value the environmental quality of the goods:
-
(i) when
 $\Theta \leq \Theta _{1}$
, the tax instrument is socially more efficient than the campaign.
$\Theta \leq \Theta _{1}$
, the tax instrument is socially more efficient than the campaign. -
(ii) When
 $\Theta \in (\Theta _{1},\Theta_{2})$
, the tax instrument prevails as long as the cost of the campaign is sufficiently high. For a relatively low cost of the campaign, taxation is preferred only if the quality ratio q
H
/q
L
is not excessive. When the quality ratio is high, there exists a threshold level for the polluting emissions above which the campaign is preferred.
$\Theta \in (\Theta _{1},\Theta_{2})$
, the tax instrument prevails as long as the cost of the campaign is sufficiently high. For a relatively low cost of the campaign, taxation is preferred only if the quality ratio q
H
/q
L
is not excessive. When the quality ratio is high, there exists a threshold level for the polluting emissions above which the campaign is preferred. -
(iii) When
 $\Theta \geq \Theta _{2}$
, the campaign is socially more efficient than the tax instrument, unless both the cost of the campaign and the emission levels are sufficiently high.
$\Theta \geq \Theta _{2}$
, the campaign is socially more efficient than the tax instrument, unless both the cost of the campaign and the emission levels are sufficiently high.
Proof: See the appendix. □
The above proposition reveals that an indirect instrument such as an environmental campaign can be more efficient than a direct tax levied on the brown good. The two preconditions for this to occur are: (i) the cost of the campaign is not too excessive, and (ii) the average valuation of the environmental quality in the market is sufficiently high (
![]() $\Theta \geq \Theta _{1}$
). While the first precondition is trivial, the second one is less obvious. In particular, it highlights that the green expansion effect of the environmental campaign increases in Θ: the higher the average valuation for the environmental quality, the larger the number of consumers willing to buy the green good. For a given cost s, an increase in Θ improves the effectiveness of the campaign in inducing some consumers to switch from the brown to the green product, thereby reducing the polluting emissions.
$\Theta \geq \Theta _{1}$
). While the first precondition is trivial, the second one is less obvious. In particular, it highlights that the green expansion effect of the environmental campaign increases in Θ: the higher the average valuation for the environmental quality, the larger the number of consumers willing to buy the green good. For a given cost s, an increase in Θ improves the effectiveness of the campaign in inducing some consumers to switch from the brown to the green product, thereby reducing the polluting emissions.
More precisely, for relatively low values of Θ (
![]() $\Theta \leq \Theta_{1}$
), the green expansion effect is almost irrelevant, and taxing the polluting product is preferred from the social standpoint. In contrast, for high values of Θ (
$\Theta \leq \Theta_{1}$
), the green expansion effect is almost irrelevant, and taxing the polluting product is preferred from the social standpoint. In contrast, for high values of Θ (
![]() $\Theta \geq \Theta _{2}$
), such an effect becomes crucial and the campaign turns out to be more efficient than the tax, provided that its cost is not exaggerated. Finally, when
$\Theta \geq \Theta _{2}$
), such an effect becomes crucial and the campaign turns out to be more efficient than the tax, provided that its cost is not exaggerated. Finally, when
![]() $\Theta \in (\Theta_{1},\Theta_{2}) $
, the green expansion effect takes intermediate values and the comparison between the two instruments includes more elements which tend to either reinforce or stifle the relevancy of such an effect. Again, taxation prevails when s is high. On the contrary, when the campaign is relatively affordable, we find that the quality ratio q
H
/q
L
may compensate for Θ. In particular, when q
H
/q
L
is sufficiently high, i.e., the brown good is very distant from the green one in terms of the quality valued by environmentally concerned consumers, then the campaign can be welfare improving as compared to the tax instrument, especially if e exceeds a certain value.Footnote
18
The explanation relies on the fact that a relatively inexpensive campaign can reduce the consumption of a good whose (environmental) quality is very low, and this becomes even more relevant when the polluting emission that it releases is considered as extremely dangerous.
$\Theta \in (\Theta_{1},\Theta_{2}) $
, the green expansion effect takes intermediate values and the comparison between the two instruments includes more elements which tend to either reinforce or stifle the relevancy of such an effect. Again, taxation prevails when s is high. On the contrary, when the campaign is relatively affordable, we find that the quality ratio q
H
/q
L
may compensate for Θ. In particular, when q
H
/q
L
is sufficiently high, i.e., the brown good is very distant from the green one in terms of the quality valued by environmentally concerned consumers, then the campaign can be welfare improving as compared to the tax instrument, especially if e exceeds a certain value.Footnote
18
The explanation relies on the fact that a relatively inexpensive campaign can reduce the consumption of a good whose (environmental) quality is very low, and this becomes even more relevant when the polluting emission that it releases is considered as extremely dangerous.
3. Hedonic qualities
Is it always the case that consumers prefer environmentally friendly goods rather than polluting ones? What would happen if brown goods outperformed their green counterparts, and consumers only cared about the performance of a certain good? In this section we address these issues by assuming that consumers value the hedonic quality of the goods above all else. It follows that, in this new scenario, good H is of high quality yet brown, while good L is of low quality yet green. More precisely, good H has a higher performance than good L but it emits pollution, thereby generating the environmental damage D=e·x H , where x H is the quantity produced by brown firm H. Recall that the green good is emission-free by assumption.
The government may intervene to reduce the environmental damage for any given level of the per-unit emissions either by taxing the polluting good, or by creating environmental awareness through the campaign. Accordingly, we develop another two-stage game in which the policy maker decides at the first stage whether to intervene and which policy instrument to use, having anticipated the price game played by firms in the second stage.
The formal analysis is only apparently similar to the one previously presented. Indeed, we are about to show that the environmental campaign has different implications, especially in terms of equilibrium market coverage and consumer surplus. For this reason, we illustrate the complete analysis of the two different policy instruments.
3.1. Supporting the environmental campaign
Consider first the environmental campaign. As introduced before, a new term appears in the indirect utility, namely γ>0, which multiplies the quality gap. This time, however, activating relative preferences implies a reduction in the utility from buying the high (but brown) quality good and a simultaneous increase in the utility from buying the low (but green) quality one. Hence, consumers experience a conflict between their initial valuation of quality and the relative preferences. Formally, this is represented by the following utility for a consumer of type
![]() $\theta \in [0,\Theta]$
:
$\theta \in [0,\Theta]$
:
 $$U(\theta) = \left\{\matrix{\theta q_{H} - p_{H} - \gamma (q_{H}-q_{L}), \hfill & \hbox{if she buys the high-quality good}, \hfill \cr \theta q_{L}-p_{L}+\gamma (q_{H}-q_{L}), \hfill & \hbox{if she buys the low-quality good}, \hfill \cr 0, \hfill & \hbox{if she refrains from buying.}\hfill}\right.$$
$$U(\theta) = \left\{\matrix{\theta q_{H} - p_{H} - \gamma (q_{H}-q_{L}), \hfill & \hbox{if she buys the high-quality good}, \hfill \cr \theta q_{L}-p_{L}+\gamma (q_{H}-q_{L}), \hfill & \hbox{if she buys the low-quality good}, \hfill \cr 0, \hfill & \hbox{if she refrains from buying.}\hfill}\right.$$
The hedonic qualities of the two goods are indicated by q H >q L . Parameter θ now measures consumers’ valuation for the hedonic quality, and Θ>0 captures consumer heterogeneity as well as the average valuation of the hedonic quality in the market.
Indifferent consumers are respectively given by:
Demands are again
![]() $x_{L} = \theta_{H} - \theta_{L}$
and
$x_{L} = \theta_{H} - \theta_{L}$
and
![]() $x_{H} = \Theta - \theta_{H}$
. Notice that, given prices, the market share of the green firm L increases in γ. This happens for two reasons. On the one hand, the consumer indifferent between not buying at all and buying the low quality (θ
L
) shifts leftward. On the other hand, the consumer indifferent between buying the low quality and the high quality (θ
H
) shifts rightward. In the case of hedonic qualities, the green expansion effect does not consist only of gaining market share at the expense of the brown rival (stealing effect), but it also includes a market coverage effect. This latter effect refers to the fact that some consumers who were not buying in the absence of the campaign are now willing to buy the good L. Hence, contrary to the previous scenario, the market can (hypothetically) be covered, as the consumer of type θ=0 may have a positive utility from buying good L if
$x_{H} = \Theta - \theta_{H}$
. Notice that, given prices, the market share of the green firm L increases in γ. This happens for two reasons. On the one hand, the consumer indifferent between not buying at all and buying the low quality (θ
L
) shifts leftward. On the other hand, the consumer indifferent between buying the low quality and the high quality (θ
H
) shifts rightward. In the case of hedonic qualities, the green expansion effect does not consist only of gaining market share at the expense of the brown rival (stealing effect), but it also includes a market coverage effect. This latter effect refers to the fact that some consumers who were not buying in the absence of the campaign are now willing to buy the good L. Hence, contrary to the previous scenario, the market can (hypothetically) be covered, as the consumer of type θ=0 may have a positive utility from buying good L if
![]() $\gamma (q_{H} - q_{L}) \gt p_{L}$
. However, we can show that this is not compatible with p
H
>p
L
.Footnote
19
We focus therefore on the uncovered market situation, although the market coverage increases in γ (θ
L
moves to the left).
$\gamma (q_{H} - q_{L}) \gt p_{L}$
. However, we can show that this is not compatible with p
H
>p
L
.Footnote
19
We focus therefore on the uncovered market situation, although the market coverage increases in γ (θ
L
moves to the left).
Producing the low-quality (green) good still requires a per-unit cost
![]() $c>0$
, while the high-quality (brown) is produced at zero cost.Footnote
20
According to the previous discussion, profit functions can be expressed as
$c>0$
, while the high-quality (brown) is produced at zero cost.Footnote
20
According to the previous discussion, profit functions can be expressed as
![]() $\pi _{H}=x_{H}\cdot p_{H}$
and
$\pi _{H}=x_{H}\cdot p_{H}$
and
![]() $\pi _{L}=\lpar p_{L}-c\rpar x_{L}.$
Equilibrium prices can be easily obtained:
$\pi _{L}=\lpar p_{L}-c\rpar x_{L}.$
Equilibrium prices can be easily obtained:
 $$\eqalign{p_{L}^{\ast H}&= {2cq_{H}+(q_{H}-q_{L}) \lpar 2\gamma q_{H}+\Theta q_{L}\rpar \over 4q_{H}-q_{L}},\cr p_{H}^{\ast H}&= {cq_{H}+(q_{H}-q_{L}) \lsqb 2\Theta q_{H}-\gamma (3q_{H}-q_{L})\rsqb \over 4q_{H}-q_{L}},}$$
$$\eqalign{p_{L}^{\ast H}&= {2cq_{H}+(q_{H}-q_{L}) \lpar 2\gamma q_{H}+\Theta q_{L}\rpar \over 4q_{H}-q_{L}},\cr p_{H}^{\ast H}&= {cq_{H}+(q_{H}-q_{L}) \lsqb 2\Theta q_{H}-\gamma (3q_{H}-q_{L})\rsqb \over 4q_{H}-q_{L}},}$$
where additional superscript H indicates hedonic qualities. Let us now define:
 $$\eqalign{\underline{\Theta}^{H} &\equiv {c(2q_{H} - q_{L}) \over q_{L}(q_{H} - q_{L})}, \cr \overline{\gamma}^{H} &\equiv \min \left\{{\Theta (2q_{H}-q_{L}) (q_{H}-q_{L}) -cq_{H} \over (5q_{H} - q_{L}) (q_{H} - q_{L})}, {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L})} \right\}\!.}$$
$$\eqalign{\underline{\Theta}^{H} &\equiv {c(2q_{H} - q_{L}) \over q_{L}(q_{H} - q_{L})}, \cr \overline{\gamma}^{H} &\equiv \min \left\{{\Theta (2q_{H}-q_{L}) (q_{H}-q_{L}) -cq_{H} \over (5q_{H} - q_{L}) (q_{H} - q_{L})}, {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L})} \right\}\!.}$$
Lemma 5
The market is uncovered and both firms are active iff
![]() $\Theta \gt \underline{\Theta}^{H}$
and
$\Theta \gt \underline{\Theta}^{H}$
and
![]() $\gamma \lt \overline{\gamma}^{H}$
.
$\gamma \lt \overline{\gamma}^{H}$
.
Proof: See the appendix. □
We assume that the conditions reported in Lemma 5 hold throughout the paper. Equilibrium demands and profits are then easily found:
 $$\eqalign{x_{L}^{\ast H} &= {q_{H}\lsqb (q_{H}-q_{L}) \lpar 2\gamma q_{H}-q_{L}\rpar -c\lpar 2q_{H}-q_{L}\rpar \rsqb \over q_{L}\lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) }, x_{H}^{\ast H} = {p_{H}^{\ast H} \over (q_{H}-q_{L})}; \cr \pi _{L}^{\ast H} &= {q_{L} \over q_{H}} (q_{H}-q_{L}) \lpar x_{L}^{\ast H}\rpar ^{2}, \pi _{H}^{\ast H}= {\lpar x_{H}^{\ast H}\rpar^{2} \over (q_{H}-q_{L})}.}$$
$$\eqalign{x_{L}^{\ast H} &= {q_{H}\lsqb (q_{H}-q_{L}) \lpar 2\gamma q_{H}-q_{L}\rpar -c\lpar 2q_{H}-q_{L}\rpar \rsqb \over q_{L}\lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) }, x_{H}^{\ast H} = {p_{H}^{\ast H} \over (q_{H}-q_{L})}; \cr \pi _{L}^{\ast H} &= {q_{L} \over q_{H}} (q_{H}-q_{L}) \lpar x_{L}^{\ast H}\rpar ^{2}, \pi _{H}^{\ast H}= {\lpar x_{H}^{\ast H}\rpar^{2} \over (q_{H}-q_{L})}.}$$
By construction,
![]() $\partial x_{L}^{\ast H}/\partial \gamma \gt 0$
and
$\partial x_{L}^{\ast H}/\partial \gamma \gt 0$
and
![]() $\partial x_{H}^{\ast H}/\partial \gamma \lt 0$
. However, differently from the previous case, total output increases in γ, as
$\partial x_{H}^{\ast H}/\partial \gamma \lt 0$
. However, differently from the previous case, total output increases in γ, as
![]() $\partial (x_{L}^{\ast H}+x_{H}^{\ast H})/\partial \gamma \gt 0$
. This is due to a green expansion effect that combines the stealing effect with the market coverage effect, as we discussed above. In the case of hedonic qualities, consumer surplus tends to increase in γ, meaning that the environmental campaign is effective in reducing polluting emissions without jeopardizing the total amount of the good available for consumption. Hence, the campaign may contribute to navigating the tradeoff between output provision and emissions reductions that typically characterizes the taxation instrument. Remember that such a result crucially depends on the fact that the green good is emission free, as we assumed in our model. However, this would continue to hold when considering relatively low emissions coming from the green producer.
$\partial (x_{L}^{\ast H}+x_{H}^{\ast H})/\partial \gamma \gt 0$
. This is due to a green expansion effect that combines the stealing effect with the market coverage effect, as we discussed above. In the case of hedonic qualities, consumer surplus tends to increase in γ, meaning that the environmental campaign is effective in reducing polluting emissions without jeopardizing the total amount of the good available for consumption. Hence, the campaign may contribute to navigating the tradeoff between output provision and emissions reductions that typically characterizes the taxation instrument. Remember that such a result crucially depends on the fact that the green good is emission free, as we assumed in our model. However, this would continue to hold when considering relatively low emissions coming from the green producer.
The social welfare function can be written in a compact way as:
where the environmental damage is
![]() $e\cdot x_{H}^{\ast H}$
, given that firm H is now the one that pollutes.Footnote
21
The social welfare function is concave in γ if and only if
$e\cdot x_{H}^{\ast H}$
, given that firm H is now the one that pollutes.Footnote
21
The social welfare function is concave in γ if and only if
![]() $s \gt \underline{s}$
, where s is defined in (3). We compute the optimal γ level which maximizes social welfare:
$s \gt \underline{s}$
, where s is defined in (3). We compute the optimal γ level which maximizes social welfare:
 $$\eqalign{\gamma^{\ast H} = {\matrix{q_{H}\lpar cq_{H}q_{L} - 12cq_{H}^{2} - 3\Theta q_{L}^{3} + cq_{L}^{2} + 11\Theta q_{H}q_{L}^{2} - 8\Theta q_{H}^{2}q_{L}\rpar \cr + \,e\,q_{L}\lpar q_{L} - 4q_{H}\rpar \lpar q_{L} - 3q_{H} \rpar } \over s\,q_{L}\lpar q_{L} - 4q_{H}\rpar ^{2} - (q_{H} - q_{L}) \lpar 12q_{H}^{3}+2q_{L}^{3}-13q_{H} q_{L}^{2} + 19q_{H}^{2} q_{L}\rpar }.}$$
$$\eqalign{\gamma^{\ast H} = {\matrix{q_{H}\lpar cq_{H}q_{L} - 12cq_{H}^{2} - 3\Theta q_{L}^{3} + cq_{L}^{2} + 11\Theta q_{H}q_{L}^{2} - 8\Theta q_{H}^{2}q_{L}\rpar \cr + \,e\,q_{L}\lpar q_{L} - 4q_{H}\rpar \lpar q_{L} - 3q_{H} \rpar } \over s\,q_{L}\lpar q_{L} - 4q_{H}\rpar ^{2} - (q_{H} - q_{L}) \lpar 12q_{H}^{3}+2q_{L}^{3}-13q_{H} q_{L}^{2} + 19q_{H}^{2} q_{L}\rpar }.}$$
Given that
![]() $\gamma ^{\ast H}\geq 0$
and that the conditions of Lemma 5 have to be satisfied, we find:
$\gamma ^{\ast H}\geq 0$
and that the conditions of Lemma 5 have to be satisfied, we find:
Lemma 6
Assume
![]() $\overline{\gamma}^{H} = {\Theta \lpar 2q_{H} - q_{L}\rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L}\rpar (q_{H} - q_{L})}$
. Then
$\overline{\gamma}^{H} = {\Theta \lpar 2q_{H} - q_{L}\rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L}\rpar (q_{H} - q_{L})}$
. Then
![]() $\gamma ^{\ast H} \in \lbrack 0,\overline{\gamma }^{H})$
when
$\gamma ^{\ast H} \in \lbrack 0,\overline{\gamma }^{H})$
when
![]() $e\in \lbrack \underline{e}^{\gamma H},\overline{e}^{\gamma H})$
.
$e\in \lbrack \underline{e}^{\gamma H},\overline{e}^{\gamma H})$
.
Proof: See the appendix, which also provides the precise values of
![]() $\underline{e}^{\gamma H}$
and
$\underline{e}^{\gamma H}$
and
![]() $\overline{e}^{\gamma H}$
. Similar conditions would have been obtained by using
$\overline{e}^{\gamma H}$
. Similar conditions would have been obtained by using
![]() $\overline{\gamma }^{H}= {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar 2q_{H} - q_{L}\rpar (q_{H} - q_{L})}$
without changing the qualitative results of our paper. □
$\overline{\gamma }^{H}= {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar 2q_{H} - q_{L}\rpar (q_{H} - q_{L})}$
without changing the qualitative results of our paper. □
The optimal policy is γ=0 as long as the emission level is very low, since the positive effect linked to the emission reduction does not compensate for the cost of the campaign. In contrast, for very high values of the emission, the optimal policy is
![]() $\gamma = \overline{\gamma }^{H}$
. Notice that at
$\gamma = \overline{\gamma }^{H}$
. Notice that at
![]() $\gamma = \overline{\gamma}^{H}$
the demand of the high-quality firm is still positive (and hence its profit). The previous discussion is summarized into:
$\gamma = \overline{\gamma}^{H}$
the demand of the high-quality firm is still positive (and hence its profit). The previous discussion is summarized into:
Remark 3
The government optimally sets: (i) γ=0 when
![]() $e \lt \underline{e}^{\gamma H}$
; (ii)
$e \lt \underline{e}^{\gamma H}$
; (ii)
![]() $\gamma = \gamma^{\ast H}$
when
$\gamma = \gamma^{\ast H}$
when
![]() $e\in \lbrack \underline{e}^{\gamma H},\overline{e}^{\gamma H})$
; (iii)
$e\in \lbrack \underline{e}^{\gamma H},\overline{e}^{\gamma H})$
; (iii)
![]() $\gamma =\overline{\gamma}^{H}$
when
$\gamma =\overline{\gamma}^{H}$
when
![]() $e\geq \overline{e}^{\gamma H}$
.
$e\geq \overline{e}^{\gamma H}$
.
3.2. Taxing the polluting good
We consider again a standard model of vertical differentiation model, where the high-quality good is now the polluting one.Footnote
22
As before, indifferent consumers are given by
![]() $\theta _{L}=p_{L}/q_{L}$
and
$\theta _{L}=p_{L}/q_{L}$
and
![]() $\theta_{H}=(p_{H}-p_{L})/q_{H}-q_{L}$
, and producing the green good requires a constant marginal cost c>0, whereas the brown quality is produced at zero cost. However, the polluting good is subject to a per-unit tax t. Profit functions are therefore given by
$\theta_{H}=(p_{H}-p_{L})/q_{H}-q_{L}$
, and producing the green good requires a constant marginal cost c>0, whereas the brown quality is produced at zero cost. However, the polluting good is subject to a per-unit tax t. Profit functions are therefore given by
![]() $\pi _{L}=(p_{L}-c) x_{L}$
and
$\pi _{L}=(p_{L}-c) x_{L}$
and
![]() $\pi _{H}=(p_{H}-t) x_{H}$
. Equilibrium prices as a function of qualities are:
$\pi _{H}=(p_{H}-t) x_{H}$
. Equilibrium prices as a function of qualities are:
Let us now define:
Lemma 7
Both firms are active in the market iff
![]() $\Theta \gt \underline{\Theta}^{H}$
and
$\Theta \gt \underline{\Theta}^{H}$
and
![]() $t \lt \overline{t}^{H}$
.
$t \lt \overline{t}^{H}$
.
Proof: See the appendix, and recall that
![]() $\underline{\Theta }^{H}$
is defined in (7). □
$\underline{\Theta }^{H}$
is defined in (7). □
Equilibrium demands/outputs are:
 $$\eqalign{x_{L}^{\ast \ast H} &= {q_{H}\lsqb q_{L}\lpar t+\Theta q_{H}-\Theta q_{L}\rpar -c\lpar 2q_{H}-q_{L}\rpar \rsqb \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) q_{L}}, \cr x_{H}^{\ast \ast H} &= {q_{H}\lsqb 2\Theta (q_{H}-q_{L})+c\rsqb -t\lpar 2q_{H}-q_{L}\rpar \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) },}$$
$$\eqalign{x_{L}^{\ast \ast H} &= {q_{H}\lsqb q_{L}\lpar t+\Theta q_{H}-\Theta q_{L}\rpar -c\lpar 2q_{H}-q_{L}\rpar \rsqb \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) q_{L}}, \cr x_{H}^{\ast \ast H} &= {q_{H}\lsqb 2\Theta (q_{H}-q_{L})+c\rsqb -t\lpar 2q_{H}-q_{L}\rpar \over \lpar 4q_{H}-q_{L}\rpar (q_{H}-q_{L}) },}$$
and they are always positive under the conditions specified in Lemma 7. By construction,
![]() $\partial x_{H}^{\ast \ast }/\partial t \lt 0$
and
$\partial x_{H}^{\ast \ast }/\partial t \lt 0$
and
![]() $\partial x_{L}^{\ast \ast}/\partial t \gt 0$
. Moreover,
$\partial x_{L}^{\ast \ast}/\partial t \gt 0$
. Moreover,
![]() $\partial (x_{H}^{\ast \ast} +x_{L}^{\ast \ast })/\partial t \lt 0$
: taxation always shrinks total output. Equilibrium profits are given by:
$\partial (x_{H}^{\ast \ast} +x_{L}^{\ast \ast })/\partial t \lt 0$
: taxation always shrinks total output. Equilibrium profits are given by:
Social welfare as a function of t is written in a compact form as:
Algebraic calculations reveal that
![]() $SW^{\ast \ast H}\lpar t\rpar $
is concave in t. The optimal tax rate is:
$SW^{\ast \ast H}\lpar t\rpar $
is concave in t. The optimal tax rate is:
 $$t^{\ast H} = {\matrix{e(4q_{H}-q_{L})\lpar 2q_{H}-q_{L}\rpar \cr[3pt] -\,q_{H}\lsqb \Theta \lpar 4q_{H}-3q_{L}\rpar (q_{H}-q_{L}) +2c\lpar 2q_{H}-q_{L}\rpar \rsqb } \over q_{H}\lpar 4q_{H}-3q_{L}\rpar }.$$
$$t^{\ast H} = {\matrix{e(4q_{H}-q_{L})\lpar 2q_{H}-q_{L}\rpar \cr[3pt] -\,q_{H}\lsqb \Theta \lpar 4q_{H}-3q_{L}\rpar (q_{H}-q_{L}) +2c\lpar 2q_{H}-q_{L}\rpar \rsqb } \over q_{H}\lpar 4q_{H}-3q_{L}\rpar }.$$
Taking into account that t* H has to be non-negative, and that the conditions appearing in Lemma 7 have to be satisfied:
Lemma 8
![]() $t^{\ast H}\in \lbrack 0,\overline{t}^{H})$
when
$t^{\ast H}\in \lbrack 0,\overline{t}^{H})$
when
![]() $e\in \lbrack \underline{e}^{tH},\overline{e}^{tH})$
.
$e\in \lbrack \underline{e}^{tH},\overline{e}^{tH})$
.
Proof: See the appendix, which also gives the precise values of
![]() $\underline{e}^{tH}$
and
$\underline{e}^{tH}$
and
![]() $\overline{e}^{tH}$
. Recall also that the precise expression of
$\overline{e}^{tH}$
. Recall also that the precise expression of
![]() $\overline{t}^{H}$
can be found in (9). □
$\overline{t}^{H}$
can be found in (9). □
Remark 4
The government optimally sets: (i) t=0 when
![]() $e \lt \underline{e}^{tH}$
; (ii) t=t*
H
when
$e \lt \underline{e}^{tH}$
; (ii) t=t*
H
when
![]() $e\in \lbrack \underline{e}^{tH},\overline{e}^{tH})$
; (iii)
$e\in \lbrack \underline{e}^{tH},\overline{e}^{tH})$
; (iii)
![]() $t=\overline{t}^{H}$
when
$t=\overline{t}^{H}$
when
![]() $e\ges \overline{e}^{tH}$
.
$e\ges \overline{e}^{tH}$
.
When
![]() $t=\overline{t}^{H}$
, the profit of the high quality firm tends to zero. Also in this case it is relatively easy to prove that the government would prefer to leave an
$t=\overline{t}^{H}$
, the profit of the high quality firm tends to zero. Also in this case it is relatively easy to prove that the government would prefer to leave an
![]() $\varepsilon \rightarrow 0$
to the polluting firm, instead of pushing it off the market.
$\varepsilon \rightarrow 0$
to the polluting firm, instead of pushing it off the market.
3.3. Comparing the two instruments under hedonic qualities
As in the previous scenario, in order to compare taxation vs. campaign, we need to rank the threshold values of e that define the interval regions where different levels of social welfare occur. In the appendix we detail all the possible cases. The following proposition summarizes our results:
Proposition 2
Assume that consumers initially value the hedonic quality of the goods. If the cost of the campaign is sufficiently high (
![]() $s \gt \underline{s}$
), then the tax instrument is always preferred to the environmental campaign in order to maximize total surplus.
$s \gt \underline{s}$
), then the tax instrument is always preferred to the environmental campaign in order to maximize total surplus.
Proof: See the appendix. □
When the social welfare associated with the environmental campaign is concave (
![]() $s \gt \underline{s}$
), the government always prefers the taxation instrument. Consumers’ concern about the hedonic quality of goods prevails over the moral dimension that may have been activated by the campaign. A direct instrument like a tax on polluting goods proves therefore to be more efficient in terms of total welfare. This result is in accordance with Proposition 1, where we argue that the environmental campaign is more efficient than taxation only when consumers’ valuation of the environmental quality is sufficiently high.
$s \gt \underline{s}$
), the government always prefers the taxation instrument. Consumers’ concern about the hedonic quality of goods prevails over the moral dimension that may have been activated by the campaign. A direct instrument like a tax on polluting goods proves therefore to be more efficient in terms of total welfare. This result is in accordance with Proposition 1, where we argue that the environmental campaign is more efficient than taxation only when consumers’ valuation of the environmental quality is sufficiently high.
Nonetheless, when we examined the impact of the campaign, we noticed that the green expansion effect consists of two components – a market stealing effect (some consumers switch from the brown to the green good), and a market coverage effect (some of the consumers who did not buy before now decide to buy the green good). Total output may therefore increase. then:
Corollary 1
The campaign may be preferred to the tax instrument if the primary focus of the policy maker is the consumer surplus.
If the green product is emission free, the environmental campaign does not generate conflicts between competition authorities (aiming at fostering competition) and environmental authorities (aiming at reducing pollution); as γ increases, one observes the reduction of the emissions but not at the cost of milder competition. This is an important result of our analysis, especially because antitrust agencies often adopt consumer surplus as a measure of social welfare.
Notice finally that, under the assumptions of our model, taxation can completely eliminate the high-quality polluting firm H (or leave it with zero profit), while the environmental campaign entails a cost s which makes such an outcome undesirable. If the aim of the policy maker is to reduce pollution emissions as much as possible, then taxation provides the most effective tool.
4. A tale of two worlds
Our purpose was to examine social welfare under two different policy instruments, both aiming at reducing pollution emissions, in two different worlds – one populated by environmentally conscious citizens, and the other by those interested in the pure performance of the goods, which can be at odds with the environmental quality. The main conclusion that can be drawn when comparing Proposition 1 with Proposition 2 is that consumers’ preliminary sensitivity towards the environment is a necessary condition for the environmental campaign to prove more efficient than the pollution tax. In both our worlds, the environmental campaign is effective in reducing pollution emissions. Indeed, it shifts the buying decision of (at least) some consumers from the brown to the green good, independently of consumers’ concern about the environment. However, when compared to other instruments like the pollution tax, the campaign may not prove to be the welfare maximizing policy when the environmental concern is low and consumers mainly care about the pure performance of a product. In our model, such a preliminary concern affects the same definition of quality. For example, when consumers’ hedonic valuation prevails over their environmental dimension, the green expansion effect generated by the campaign does not compensate for its cost. A traditional instrument like the pollution tax, which is directly levied on the production of the polluting good, turns out to be more efficient. In addition, it represents a net gain for the government. For the environmental campaign to be socially preferable, we need a scenario in which consumers have already at least some positive valuation of the environmental quality.
In real-world terms, our analysis suggests the adoption of country-specific policy instruments. Extreme examples of what we have in mind are provided by Sweden and China. While the former is an early adopter of sustainable thinking and one of the few industrialized countries to have reduced its carbon emissions, the latter may well represent an example of a country where environmental protection is not a main concern.Footnote 23 Empirical support for our statement comes from the Eurostat statistics on EU countries’ tax revenues on pollution as a percentage of GDP: in 2011 the EU average was 0.11, while Sweden was well below this value (0.05).Footnote 24 On the other hand, China suffers from severe environmental damages to natural resources associated with the country's rapid economic successes. Recent measures taken by the Chinese government aim at improving its environmental situation. However, this is mainly done by resorting to traditional policy instruments.Footnote 25
We would also like to point out that our policy implications are based on total social welfare as a measure of social wellbeing. While this is a quite standard measure of welfare, a policy maker may decide to put different weights on consumer and producer surplus when evaluating a policy intervention. Our results may therefore change if we consider consumer surplus as an alternative measure of welfare. Indeed, as put forward in the model, taxation shrinks total output, thus implying that consumer surplus decreases when the government applies such a tool. This holds under both hedonic and environmental qualities. As for the environmental campaign, it has a similar effect but only under environmental qualities. On the contrary, under hedonic qualities, the effect of the campaign is to increase total output, thus expanding consumer surplus. This means that if one attaches a relatively high weight to consumer surplus, then the environmental campaign may surpass the taxation instrument in terms of efficiency even if consumers initially value the hedonic component of consumption, provided that the emission level associated with the green product is sufficiently low.
5. Discussion and robustness check
The purpose of this section is to better motivate our methodological decision to adopt vertical differentiation and discuss our technical assumptions. We also insert relative preferences in a simple horizontally differentiated duopoly and discuss the differences between the two modeling strategies. In the online appendix (see section 3), we also present an extension to the baseline model in order to show that our most important results continue to hold when consumers are endowed with an initial level of green awareness which is independent from the policy maker's intervention.
5.1. Vertical vs. horizontal differentiation
The starting point of our paper is related to the existence of two vertically differentiated ‘worlds’, depending on whether consumers prefer the environmental quality or the hedonic quality of a product. We acknowledge that in most societies environmentally and non-environmentally concerned consumers coexist with one another. For instance, imagine that a fraction δ of consumers cares about the environmental quality, whereas the complementary fraction (1−δ) values the hedonic quality. We reckon that such an extension would not add much in terms of results. We conjecture that there would exist a δ-threshold such that the campaign would prove to be more efficient than the tax instrument as long as the fraction of environmentally concerned consumers is sufficiently high (and vice versa).
A unified scenario in which consumers reveal heterogeneous environmental concern is usually represented in horizontally differentiated models. Instead, we opted for vertical differentiation in order to capture the idea that all consumers, although being heterogeneous in their willingness to pay for quality, agree on the quality ranking of the two goods. Our setting is relevant in a wide range of situations in which goods are imperfect substitutes, and their qualities (either in terms of polluting emissions or in terms of pure performance) are objectively different. In particular, by adopting two alternative definitions of quality, we showed that our results crucially depended on the degree of consumer heterogeneity, which in turn was based on the specific type of quality that we considered.
A relatively simple model of horizontal differentiation would not have allowed us to obtain similar results. Consider, for instance, an extended version of the Hotelling (Reference Hotelling1929) linear city in which two firms produce a homogeneous good (homogeneous in terms of intrinsic quality) and locate in the interval [0, 1], where the location represents the environmental impact of the good. Under horizontal differentiation, at equal prices some consumers would buy the green good and others the brown good.
In section 2 of the online appendix, we develop in detail this horizontal differentiation extension. Here we only provide a brief sketch of the model and its main results in order to make a comparison with our vertical differentiation approach. Two firms, G and B, are located at the endpoints of the interval [0, 1]. Firm G is located in 0 and produces a green product (G), while firm B is located in 1 and produces a brown product (B). Let p G and p B denote respectively the prices of products G and B, with production being costless only for the brown producer. As for the demand side, we assume a continuum of consumers of mass 1 uniformly distributed along the interval [0, 1]. Each of them buys one unit of the good. The utility of a consumer indexed by x∈[0, 1] is:
where v is the intrinsic quality of the goods and r represents the linear transportation cost measuring the substitutability between the two goods. In line with our model, buying the green (brown) good amplifies (reduces) the satisfaction of consumption by the term γ (1−0). This term depends on the environmental distance between the goods (1−0) as well as on the level of personal moral norms that favor pro-environmental behaviors, captured by γ≥0. As in the baseline model, γ is induced by the policy maker through the support of a costly environmental campaign. When the tax instrument is implemented, γ goes to 0. Profit functions and social welfare replicate those in the baseline model. The environmental damage derives again only from the production activity of the brown firm.
By replicating the two-stage game, we evaluate the social efficiency of the two policy instruments. We prove that taxation is more efficient than the campaign for a relatively wide interval region. The campaign prevails only when both its cost and the cost for producing the green product are sufficiently low, provided that the emissions take an intermediate value. Notice that, although it is still possible to find an interval region in which the policy maker prefers to adopt the campaign, this mainly depends upon a cost-effectiveness analysis, not upon consumers’ environmental concern. In our baseline model the impact of Θ was in a certain way ‘asymmetric’. The higher its value, the higher the consumer heterogeneity, but also the higher the average (and maximal) willingness to pay for quality. This undoubtedly favors the high-quality firm (which in our framework could be either the green or the brown firm). In the Hotelling model, parameter r could somewhat measure consumers’ heterogeneity, given that when it increases the two goods are perceived as more differentiated. However, r acts in a symmetric way, as it does not convey any particular advantage to a specific producer. For this reason, a ‘horizontal’ measure of consumer heterogeneity does not play any role in comparing the social efficiency of the two policy instruments.
Contributions that are close to the formal model presented in this section are those by Conrad (Reference Conrad2005) and Espìnola-Arredondo and Zhao (Reference Espìnola-Arredondo and Zhao2012), who extend the Hotelling duopoly model by taking into account green consumerism. Moreover, they also assume that the market is covered, thus simplifying the formal analysis.Footnote 26 In terms of a comparison with our baseline model, the main drawback of considering market coverage is that total output at equilibrium is fixed. It follows that the comparison between the two instruments could be biased in favor of the taxation instrument as it no longer entails the negative effect of shrinking total output.
5.2. Effectiveness and cost of the environmental campaign
In the baseline model we restricted our attention to sufficiently low levels of γ. This ensured that both firms remained active in the market and that the initial quality ranking did not reverse. In particular, in the case of environmental qualities, if
![]() $\gamma \gt \overline{\gamma }^{E}$
the low (brown) quality firm would leave the market. In contrast, with hedonic qualities, if
$\gamma \gt \overline{\gamma }^{E}$
the low (brown) quality firm would leave the market. In contrast, with hedonic qualities, if
![]() $\gamma \gt \overline{\gamma }^{H}$
the low (green) quality firm would charge a higher price than the rival, and eventually we would observe a quality switch. Therefore, in order to keep the initial ranking of hedonic qualities, we assume that the campaign cannot be too ‘revolutionary’, i.e., it does not induce all consumers to switch to the green good.Footnote
27
However, our results are robust to this assumption. On the one hand, under environmental qualities, it does not make sense to further pursue the campaign. Once the brown firm is pushed off the market, then emissions reach their minimal level. On the other hand, under hedonic qualities, extending the analysis to higher levels of γ significantly alters the equilibrium market structure. In particular, this implies shifting first from an uncovered to a covered duopoly market (at the limit), and then to a monopoly dominated by the low green quality firm.Footnote
28
Yet again, our main results hold. In the case of hedonic qualities, the tax instrument is still more efficient than the campaign. In fact, recall that pursuing high levels of the environmental campaign requires increasing costs.
$\gamma \gt \overline{\gamma }^{H}$
the low (green) quality firm would charge a higher price than the rival, and eventually we would observe a quality switch. Therefore, in order to keep the initial ranking of hedonic qualities, we assume that the campaign cannot be too ‘revolutionary’, i.e., it does not induce all consumers to switch to the green good.Footnote
27
However, our results are robust to this assumption. On the one hand, under environmental qualities, it does not make sense to further pursue the campaign. Once the brown firm is pushed off the market, then emissions reach their minimal level. On the other hand, under hedonic qualities, extending the analysis to higher levels of γ significantly alters the equilibrium market structure. In particular, this implies shifting first from an uncovered to a covered duopoly market (at the limit), and then to a monopoly dominated by the low green quality firm.Footnote
28
Yet again, our main results hold. In the case of hedonic qualities, the tax instrument is still more efficient than the campaign. In fact, recall that pursuing high levels of the environmental campaign requires increasing costs.
Turning our attention to the cost of the campaign, we assumed that
![]() $s \gt \underline{s}$
, thus ensuring the concavity of the social welfare function. This allowed us to determine the optimal investment level in the campaign. For
$s \gt \underline{s}$
, thus ensuring the concavity of the social welfare function. This allowed us to determine the optimal investment level in the campaign. For
![]() $s \lt \underline{s}$
, the social welfare function is convex in γ, meaning that the optimal campaign level is reached either in γ=0 or in
$s \lt \underline{s}$
, the social welfare function is convex in γ, meaning that the optimal campaign level is reached either in γ=0 or in
![]() $\gamma = \overline{\gamma}$
. Considering hedonic qualities, it is possible to demonstrate that, when
$\gamma = \overline{\gamma}$
. Considering hedonic qualities, it is possible to demonstrate that, when
![]() $s \lt \underline{s}$
, there are conditions for which a relatively cheap campaign can be more efficient than the pollution tax. In particular, this is more likely to happen for high values of Θ, i.e., when consumers’ ex ante heterogeneity is prominent. However, as both goods are still on the market, the emission level should not be perceived as too dangerous by the policy maker; otherwise a more direct taxation instrument is to be preferred. In contrast, with environmental qualities our qualitative results do not change, the campaign being more efficient than the tax instrument in an interval region comparable to that of the baseline model.
$s \lt \underline{s}$
, there are conditions for which a relatively cheap campaign can be more efficient than the pollution tax. In particular, this is more likely to happen for high values of Θ, i.e., when consumers’ ex ante heterogeneity is prominent. However, as both goods are still on the market, the emission level should not be perceived as too dangerous by the policy maker; otherwise a more direct taxation instrument is to be preferred. In contrast, with environmental qualities our qualitative results do not change, the campaign being more efficient than the tax instrument in an interval region comparable to that of the baseline model.
6. Conclusions
We have considered two different worlds, depending on whether consumers are ex ante affected by environmental concerns or not. We have compared the adoption of conventional tax on the emission of pollution with an environmental campaign which stigmatizes the consumption of the brown good, while at the same time rewarding the consumption of the green product. Both policy instruments are effective in reducing polluting emissions. However, their relative efficiency from a social welfare point of view changes according to the consumer's environmental sensitivity. We have proved that, if consumers value the hedonic dimension of quality above all, then the tax instrument is more efficient than the campaign. On the contrary, when consumers appreciate the environmental dimension of consumption, the campaign may be preferred, but only if the average valuation for the environmental quality is sufficiently high. Interestingly, we also found that, if consumer surplus were the primary focus of the policy maker, then a campaign could be more efficient than taxation even when consumers value the hedonic quality.
In the last part we discussed the robustness of the main assumptions of our model together with its main limitations. All in all, we believe that our paper represents an interesting starting point from which to evaluate the relative performance of environmental awareness campaigns vis à vis traditional policy instruments. Additional theoretical and empirical research must be carried out with the aim of providing accurate results, thereby helping the policy maker in designing the best-suited instrument to curb pollution emission while achieving the highest level of social welfare.
On theoretical grounds, there are at least two interesting extensions of our research that deserve attention. The first one is related to the potential dynamic efficiency of environmental campaigns. Indeed, there exist situations in which consumers characterized by a strong bias towards the hedonic quality seem not to respond to environmental campaigns, at least in the short run. Still, although the campaign may not pay off in the short term, environmental concern may gradually become ingrained in the social consciousness, especially if it is combined with an investment in environmental education. This ‘planting of the seeds’ may contribute to the success of future environmental campaigns. Schumacher (Reference Schumacher2015) investigates the surge in environmental culture across the globe. He finds that only when societies reach a certain level of economic development do they decide to invest in adopting an environmental culture. Thus, we should compare the static efficiency of the tax with the dynamic efficiency of the campaign.Footnote 29 In addition, dynamic models can be used to explore the idea that the cost of the campaign could decrease over time. This is particularly related to the case of expensive and lengthy environmental educational campaigns that aim at redefining the concept of quality.
The second extension regards the possibility of allowing for price discrimination. Liu and Serfes (Reference Liu and Serfes2005) consider a vertically differentiated covered duopoly in which firms can either develop or acquire a database with the aim of segmenting consumers into distinct groups. Firms can then tailor their prices to each consumer segment (third-degree price discrimination). The authors show that (i) only the high-quality firm has an incentive to acquire information and practice price discrimination; and (ii) not only its profit, but also social (and consumer) welfare monotonically increase with the information precision. In terms of our problem, the effect of price discrimination on social welfare would depend on consumer environmental concern. Under environmental qualities, the incentive for the high-and-green quality firm to price discriminate would be a fortiori welfare improving with information precision. In contrast, under hedonic qualities, where the high-quality firm is the brown firm, this kind of price discrimination may have ambiguous welfare effects as it would increase pollution with respect to uniform pricing.
Supplementary material and methods
To view supplementary material for this article, please visit https://doi.org/10.1017/S1355770X16000371.
Appendix
Proof of Lemma 1
To start with, notice that:
 $$\eqalign{& p_{L}^{\ast E} \gt 0\iff \gamma \lt {q_{L}\lsqb c + \Theta (q_{H} - q_{L}) \rsqb \over 2q_{H}(q_{H} - q_{L})} \equiv \overline{\gamma}^{E}, \cr & p_{H}^{\ast E} - c \gt 0 \iff \gamma \gt {c\lpar 2q_{H}-q_{L}\rpar -2q_{H}\Theta (q_{H}-q_{L}) \over \lpar 3q_{H}-q_{L}\rpar (q_{H}-q_{L})} \equiv \underline{\gamma}^{E}, \cr & p_{H}^{\ast E} - p_{L}^{\ast E} = {\lpar q_{L} - 2q_{H} \rpar \lpar \Theta q_{L} - \Theta q_{H} - c \rpar + \gamma \lpar q_{L} - 5q_{H} \rpar \lpar q_{L} - q_{H} \rpar \over \lpar 4q_{H} - q_{L} \rpar } \gt 0.}$$
$$\eqalign{& p_{L}^{\ast E} \gt 0\iff \gamma \lt {q_{L}\lsqb c + \Theta (q_{H} - q_{L}) \rsqb \over 2q_{H}(q_{H} - q_{L})} \equiv \overline{\gamma}^{E}, \cr & p_{H}^{\ast E} - c \gt 0 \iff \gamma \gt {c\lpar 2q_{H}-q_{L}\rpar -2q_{H}\Theta (q_{H}-q_{L}) \over \lpar 3q_{H}-q_{L}\rpar (q_{H}-q_{L})} \equiv \underline{\gamma}^{E}, \cr & p_{H}^{\ast E} - p_{L}^{\ast E} = {\lpar q_{L} - 2q_{H} \rpar \lpar \Theta q_{L} - \Theta q_{H} - c \rpar + \gamma \lpar q_{L} - 5q_{H} \rpar \lpar q_{L} - q_{H} \rpar \over \lpar 4q_{H} - q_{L} \rpar } \gt 0.}$$
Next, we insert
![]() $p_{L}^{\ast E}$
and
$p_{L}^{\ast E}$
and
![]() $p_{H}^{\ast E}$
into θ
L
and θ
H
to verify that
$p_{H}^{\ast E}$
into θ
L
and θ
H
to verify that
![]() $0 \lt \theta_{L}^{\ast E} \lt \theta_{H}^{\ast E} \lt \Theta$
:
$0 \lt \theta_{L}^{\ast E} \lt \theta_{H}^{\ast E} \lt \Theta$
:
 $$\eqalign{&\theta_{L}^{\ast E} = {q_{L}\lpar c + \Theta q_{H} - \Theta q_{L} \rpar + \gamma \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0, \hbox{always;} \cr &\theta_{H}^{\ast E} - \theta_{L}^{\ast E} \gt 0 \iff \gamma \lt \overline{\gamma}^{E}; \quad \Theta - \theta _{H} \gt 0 \iff \gamma \gt \underline{\gamma }^{E}.}$$
$$\eqalign{&\theta_{L}^{\ast E} = {q_{L}\lpar c + \Theta q_{H} - \Theta q_{L} \rpar + \gamma \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0, \hbox{always;} \cr &\theta_{H}^{\ast E} - \theta_{L}^{\ast E} \gt 0 \iff \gamma \lt \overline{\gamma}^{E}; \quad \Theta - \theta _{H} \gt 0 \iff \gamma \gt \underline{\gamma }^{E}.}$$
As usual in these models,
![]() $0 \lt \theta _{L}^{\ast E} \lt \theta_{H}^{\ast E} \lt \Theta$
also guarantees that both firms are active in the market. Notice that
$0 \lt \theta _{L}^{\ast E} \lt \theta_{H}^{\ast E} \lt \Theta$
also guarantees that both firms are active in the market. Notice that
![]() $\underline{\gamma }^{E} \gt 0$
iff
$\underline{\gamma }^{E} \gt 0$
iff
![]() $\Theta \lt {c\lpar 2q_{H} - q_{L} \rpar \over 2q_{H}(q_{H} - q_{L})} \equiv \underline{\Theta}^{E}$
. Therefore, assuming that
$\Theta \lt {c\lpar 2q_{H} - q_{L} \rpar \over 2q_{H}(q_{H} - q_{L})} \equiv \underline{\Theta}^{E}$
. Therefore, assuming that
![]() $\Theta \gt \underline{\Theta}^{E}$
implies that
$\Theta \gt \underline{\Theta}^{E}$
implies that
![]() $\underline{\gamma}^{E}$
is negative, and then
$\underline{\gamma}^{E}$
is negative, and then
![]() $\theta_{H} \lt \Theta$
always holds. To sum up, the conditions that have to be simultaneously satisfied are
$\theta_{H} \lt \Theta$
always holds. To sum up, the conditions that have to be simultaneously satisfied are
![]() $\Theta \gt \underline{\Theta }^{E}$
and
$\Theta \gt \underline{\Theta }^{E}$
and
![]() $\gamma \lt \overline{\gamma}^{E}.$
$\gamma \lt \overline{\gamma}^{E}.$
Proof of Lemma 2
From (4),
![]() $\gamma^{\ast E} \geq 0$
iff
$\gamma^{\ast E} \geq 0$
iff
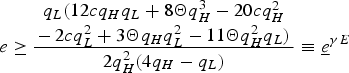 $e \geq {\matrix{q_{L}(12cq_{H}q_{L} + 8 \Theta q_{H}^{3} - 20cq_{H}^{2} \cr -\,2cq_{L}^{2} + 3\Theta q_{H}q_{L}^{2} - 11 \Theta q_{H}^{2} q_{L})} \over 2q_{H}^{2}\lpar 4q_{H} - q_{L}\rpar } \equiv \underline{e}^{\gamma E}$
; however,
$e \geq {\matrix{q_{L}(12cq_{H}q_{L} + 8 \Theta q_{H}^{3} - 20cq_{H}^{2} \cr -\,2cq_{L}^{2} + 3\Theta q_{H}q_{L}^{2} - 11 \Theta q_{H}^{2} q_{L})} \over 2q_{H}^{2}\lpar 4q_{H} - q_{L}\rpar } \equiv \underline{e}^{\gamma E}$
; however,
![]() $\underline{e}^{\gamma E}\geq 0$
iff
$\underline{e}^{\gamma E}\geq 0$
iff
![]() $\Theta \leq \widetilde{\Theta} = {2c(10q_{H}^{2} - 6q_{H} q_{L} + q_{L}^{2}) \over q_{H} (q_{H} - q_{L}) \lpar 8q_{H} - 3q_{L} \rpar }$
, with
$\Theta \leq \widetilde{\Theta} = {2c(10q_{H}^{2} - 6q_{H} q_{L} + q_{L}^{2}) \over q_{H} (q_{H} - q_{L}) \lpar 8q_{H} - 3q_{L} \rpar }$
, with
![]() $\widetilde{\Theta} \gt \underline{\Theta}^{E}$
. It follows that
$\widetilde{\Theta} \gt \underline{\Theta}^{E}$
. It follows that
![]() $\gamma^{\ast E} \geq 0$
always for
$\gamma^{\ast E} \geq 0$
always for
![]() $\Theta \geq \widetilde{\Theta}$
, while in
$\Theta \geq \widetilde{\Theta}$
, while in
![]() $\Theta \in (\underline{\Theta}^{E}, \widetilde{\Theta})$
we have that
$\Theta \in (\underline{\Theta}^{E}, \widetilde{\Theta})$
we have that
![]() $\gamma^{\ast E} \geq 0$
when
$\gamma^{\ast E} \geq 0$
when
![]() $e \geq \underline{e}^{\gamma E}(\gt 0)$
. In order to avoid notational complications, we can write that
$e \geq \underline{e}^{\gamma E}(\gt 0)$
. In order to avoid notational complications, we can write that
![]() $\gamma ^{\ast E}\geq 0$
when
$\gamma ^{\ast E}\geq 0$
when
![]() $e\geq \max \{0,\underline{e}^{\gamma E}\}$
. Secondly,
$e\geq \max \{0,\underline{e}^{\gamma E}\}$
. Secondly,
![]() $\gamma ^{\ast E} \lt \overline{\gamma}^{E}$
iff
$\gamma ^{\ast E} \lt \overline{\gamma}^{E}$
iff
![]() $e \lt \overline{e}^{\gamma E}$
, where
$e \lt \overline{e}^{\gamma E}$
, where
 $\overline{e}^{\gamma E}= {\matrix{q_{L}\{ \lpar 7q_{H} - 2q_{L} \rpar (q_{H} - q_{L})^{2} \lsqb c - \Theta (q_{H} - q_{L}) \rsqb \cr + \lsqb c + \Theta \,s(q_{H} - q_{L}) \rsqb \lpar 4q_{H} - q_{L} \rpar q_{L}\}} \over 4q_{H}^{3}(q_{H} - q_{L})}$
.
$\overline{e}^{\gamma E}= {\matrix{q_{L}\{ \lpar 7q_{H} - 2q_{L} \rpar (q_{H} - q_{L})^{2} \lsqb c - \Theta (q_{H} - q_{L}) \rsqb \cr + \lsqb c + \Theta \,s(q_{H} - q_{L}) \rsqb \lpar 4q_{H} - q_{L} \rpar q_{L}\}} \over 4q_{H}^{3}(q_{H} - q_{L})}$
.
Proof of Lemma 3
We focus on the case in which
![]() $p_{H}^{\ast \ast E}>p_{L}^{\ast \ast E}$
:
$p_{H}^{\ast \ast E}>p_{L}^{\ast \ast E}$
:
Moreover, we have to guarantee that at equilibrium prices
![]() $p_{H}^{\ast \ast E}$
and
$p_{H}^{\ast \ast E}$
and
![]() $p_{L}^{\ast \ast E}$
both firms are active in the market. This implies
$p_{L}^{\ast \ast E}$
both firms are active in the market. This implies
![]() $0 \lt \theta_{L}^{\ast \ast E} \lt \theta_{H}^{\ast \ast E} \lt \Theta$
:
$0 \lt \theta_{L}^{\ast \ast E} \lt \theta_{H}^{\ast \ast E} \lt \Theta$
:
 $$\eqalign{\theta_{L}^{\ast \ast E} &= {[cq_{L} + 2tq_{H} + q_{L} \Theta (q_{H} - q_{L})] \over q_{L} \lpar 4q_{H} - q_{L} \rpar } \gt 0, \cr \theta_{L}^{\ast \ast E} - \theta_{H}^{\ast \ast E} &= {[cq_{L} - t\lpar 2q_{H} - q_{L}\rpar + \Theta q_{H}q_{L} - \Theta q_{L}^{2}] q_{H} \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L} \rpar q_{L}} \lt 0 \cr &\iff t \lt {q_{L} \lsqb c + \Theta (q_{H} - q_{L}) \rsqb \over \lpar 2q_{H} - q_{L} \rpar } \equiv \overline{t}^{E} \lt \widehat{t}, \cr \theta_{H}^{\ast \ast E} - \Theta &= {c(2q_{H} - q_{L}) - tq_{H} - 2\Theta q_{H}(q_{H} - q_{L}) \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L}\rpar } \lt 0 \cr &\iff t \gt {c(2q_{H} - q_{L}) - 2\Theta q_{H}(q_{H} - q_{L}) \over q_{H}} \equiv \underline{t}^{E}.}$$
$$\eqalign{\theta_{L}^{\ast \ast E} &= {[cq_{L} + 2tq_{H} + q_{L} \Theta (q_{H} - q_{L})] \over q_{L} \lpar 4q_{H} - q_{L} \rpar } \gt 0, \cr \theta_{L}^{\ast \ast E} - \theta_{H}^{\ast \ast E} &= {[cq_{L} - t\lpar 2q_{H} - q_{L}\rpar + \Theta q_{H}q_{L} - \Theta q_{L}^{2}] q_{H} \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L} \rpar q_{L}} \lt 0 \cr &\iff t \lt {q_{L} \lsqb c + \Theta (q_{H} - q_{L}) \rsqb \over \lpar 2q_{H} - q_{L} \rpar } \equiv \overline{t}^{E} \lt \widehat{t}, \cr \theta_{H}^{\ast \ast E} - \Theta &= {c(2q_{H} - q_{L}) - tq_{H} - 2\Theta q_{H}(q_{H} - q_{L}) \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L}\rpar } \lt 0 \cr &\iff t \gt {c(2q_{H} - q_{L}) - 2\Theta q_{H}(q_{H} - q_{L}) \over q_{H}} \equiv \underline{t}^{E}.}$$
By construction, the above conditions also guarantee that
![]() $p_{H}^{\ast \ast E} \gt c$
and
$p_{H}^{\ast \ast E} \gt c$
and
![]() $p_{L}^{\ast \ast E} \gt t$
. Moreover,
$p_{L}^{\ast \ast E} \gt t$
. Moreover,
![]() $\underline{t}^{E} \lt 0$
iff
$\underline{t}^{E} \lt 0$
iff
![]() $\Theta \gt \underline{\Theta}^{E}$
. Hence, both firms are active iff
$\Theta \gt \underline{\Theta}^{E}$
. Hence, both firms are active iff
![]() $t \lt \overline{t}^{E}$
and
$t \lt \overline{t}^{E}$
and
![]() $\Theta \gt \underline{\Theta}^{E}$
.
$\Theta \gt \underline{\Theta}^{E}$
.
Proof of Lemma 4
From (6), we easily obtain that
![]() $t^{\ast E}\geq 0$
iff
$t^{\ast E}\geq 0$
iff
 $e\geq \underline{e}^{tE}= {\matrix{q_{L}[2c\lpar 2q_{H}-q_{L}\rpar \cr-\Theta q_{L}(q_{H}-q_{L})]} \over \lpar 4q_{H}-q_{L}\rpar \lpar 2q_{H}-q_{L}\rpar }$
. However,
$e\geq \underline{e}^{tE}= {\matrix{q_{L}[2c\lpar 2q_{H}-q_{L}\rpar \cr-\Theta q_{L}(q_{H}-q_{L})]} \over \lpar 4q_{H}-q_{L}\rpar \lpar 2q_{H}-q_{L}\rpar }$
. However,
![]() $\underline{e}^{tE}\geq 0$
iff
$\underline{e}^{tE}\geq 0$
iff
![]() $\Theta \leq {2c\lpar 2q_{H}-q_{L}\rpar \over q_{L}(q_{H}-q_{L}) }\equiv \widehat{\Theta}$
. In order to avoid unnecessary notational complications, we write:
$\Theta \leq {2c\lpar 2q_{H}-q_{L}\rpar \over q_{L}(q_{H}-q_{L}) }\equiv \widehat{\Theta}$
. In order to avoid unnecessary notational complications, we write:
![]() $t^{\ast E}\geq 0$
when
$t^{\ast E}\geq 0$
when
![]() $e\geq \max \{0,\underline{e}^{tE}\}.$
Secondly, notice that
$e\geq \max \{0,\underline{e}^{tE}\}.$
Secondly, notice that
![]() $t^{\ast E} \lt \overline{t}^{E}$
iff
$t^{\ast E} \lt \overline{t}^{E}$
iff
![]() $e \lt \overline{e}^{tE} = {c\lpar 2q_{H} - q_{L}\rpar + 2\Theta (q_{H} - q_{L}) ^{2} \over \lpar 2q_{H}-q_{L}\rpar }$
, with
$e \lt \overline{e}^{tE} = {c\lpar 2q_{H} - q_{L}\rpar + 2\Theta (q_{H} - q_{L}) ^{2} \over \lpar 2q_{H}-q_{L}\rpar }$
, with
![]() $\overline{e}^{tE} \gt \underline{e}^{tE}$
, as expected.
$\overline{e}^{tE} \gt \underline{e}^{tE}$
, as expected.
Proof of Proposition 1
This proof can be found in section 1 of the online appendix, together with the social welfare expressions that depend on the policy instrument adopted by the policy maker (see Remarks 1 and 2).
Proof of Lemma 5
To start with, notice that
This threshold value of γ decreases in c and increases in Θ. On the one hand, the higher c is, the more stringent the constraint, because p L becomes increasingly higher than p H . On the other hand, the higher parameter Θ is, the less binding the constraint, because consumers become increasingly heterogeneous and competition softens.Footnote 30
We have to check whether at the equilibrium prices
![]() $p_{L}^{\ast H}$
and
$p_{L}^{\ast H}$
and
![]() $p_{H}^{\ast H}$
both firms are in the market, i.e., we need to verify that
$p_{H}^{\ast H}$
both firms are in the market, i.e., we need to verify that
![]() $0 \lt \theta_{L}^{\ast H} \lt \theta_{H}^{\ast H} \lt \Theta$
:
$0 \lt \theta_{L}^{\ast H} \lt \theta_{H}^{\ast H} \lt \Theta$
:
 $$\eqalign{\theta_{L}^{\ast H} &= {2cq_{H} + (q_{H} - q_{L}) [\Theta q_{L} - \gamma (2q_{H}+q_{L})] \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0 \cr &\quad \iff \gamma \lt {2cq_{H} + \Theta (q_{H} - q_{L}) q_{L} \over (q_{H} - q_{L}) \lpar 2q_{H} - q_{L} \rpar }, \cr \theta_{H}^{\ast H} - \theta_{L}^{\ast H} &= {q_{H} \lsqb c \lpar q_{L} - 2q_{H} \rpar + (q_{H} - q_{L}) \lpar \Theta q_{L} + 2\gamma q_{H} \rpar \rsqb \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0 \cr &\quad \hbox{always when}\Theta \gt \underline{\Theta}^{H}, \cr \theta_{H}^{\ast H} - \Theta &= {\lpar q_{L} - q_{H} \rpar [2\Theta q_{H} - \gamma (3q_{H} - q_{L})] - cq_{H} \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L}\rpar } \lt 0 \cr &\quad \hbox{always when} p_{H}^{\ast H} - p_{L}^{\ast H} \gt 0.}$$
$$\eqalign{\theta_{L}^{\ast H} &= {2cq_{H} + (q_{H} - q_{L}) [\Theta q_{L} - \gamma (2q_{H}+q_{L})] \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0 \cr &\quad \iff \gamma \lt {2cq_{H} + \Theta (q_{H} - q_{L}) q_{L} \over (q_{H} - q_{L}) \lpar 2q_{H} - q_{L} \rpar }, \cr \theta_{H}^{\ast H} - \theta_{L}^{\ast H} &= {q_{H} \lsqb c \lpar q_{L} - 2q_{H} \rpar + (q_{H} - q_{L}) \lpar \Theta q_{L} + 2\gamma q_{H} \rpar \rsqb \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0 \cr &\quad \hbox{always when}\Theta \gt \underline{\Theta}^{H}, \cr \theta_{H}^{\ast H} - \Theta &= {\lpar q_{L} - q_{H} \rpar [2\Theta q_{H} - \gamma (3q_{H} - q_{L})] - cq_{H} \over (q_{H} - q_{L}) \lpar 4q_{H} - q_{L}\rpar } \lt 0 \cr &\quad \hbox{always when} p_{H}^{\ast H} - p_{L}^{\ast H} \gt 0.}$$
By construction, the above conditions also verify that
![]() $p_{H}^{\ast H} \gt 0$
and
$p_{H}^{\ast H} \gt 0$
and
![]() $p_{L}^{\ast H} \gt c$
. Assuming
$p_{L}^{\ast H} \gt c$
. Assuming
![]() $\Theta \gt \underline{\Theta}^{H}$
(see (7)), we need to compare only the two threshold values of γ appearing above. However, given that similar qualitative results will appear when using each of the two values, we can write
$\Theta \gt \underline{\Theta}^{H}$
(see (7)), we need to compare only the two threshold values of γ appearing above. However, given that similar qualitative results will appear when using each of the two values, we can write
![]() $\overline{\gamma }^{H} = \min \left\{{\Theta \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L} \rpar (q_{H} - q_{L})}, {2cq_{H} + \Theta (q_{H} - q_{L}) q_{L} \over \lpar q_{L} - 2q_{H} \rpar \lpar q_{L} - q_{H}\rpar } \right\}.$
$\overline{\gamma }^{H} = \min \left\{{\Theta \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L} \rpar (q_{H} - q_{L})}, {2cq_{H} + \Theta (q_{H} - q_{L}) q_{L} \over \lpar q_{L} - 2q_{H} \rpar \lpar q_{L} - q_{H}\rpar } \right\}.$
Proof of Lemma 6
From (8),
![]() $\gamma^{\ast H} \geq 0$
iff
$\gamma^{\ast H} \geq 0$
iff
 $e \geq \underline{e}^{\gamma H} = {\matrix{q_{H} [q_{L}\Theta (8q_{H} - 3q_{L}) (q_{H} - q_{L}) \cr + \,c( 3q_{H} - q_{L}) (4q_{H} + q_{L})]} \over q_{L}\lpar 4q_{H} - q_{L} \rpar \lpar 3q_{H} - q_{L}\rpar }$
. If
$e \geq \underline{e}^{\gamma H} = {\matrix{q_{H} [q_{L}\Theta (8q_{H} - 3q_{L}) (q_{H} - q_{L}) \cr + \,c( 3q_{H} - q_{L}) (4q_{H} + q_{L})]} \over q_{L}\lpar 4q_{H} - q_{L} \rpar \lpar 3q_{H} - q_{L}\rpar }$
. If
![]() $\overline{\gamma}^{H} = {\Theta \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L} \rpar (q_{H} - q_{L})}$
,
$\overline{\gamma}^{H} = {\Theta \lpar 2q_{H} - q_{L} \rpar (q_{H} - q_{L}) - cq_{H} \over \lpar 5q_{H} - q_{L} \rpar (q_{H} - q_{L})}$
,
![]() $\gamma^{\ast H} \lt \overline{\gamma}^{H} \iff e \lt \overline{e}^{\gamma H},$
where:
$\gamma^{\ast H} \lt \overline{\gamma}^{H} \iff e \lt \overline{e}^{\gamma H},$
where:
 $$\eqalign{\overline{e}^{\gamma H} &= {1 \over q_{L}\lpar 3q_{H}-q_{L}\rpar (q_{H}-q_{L}) \lpar 5q_{H}-q_{L}\rpar } \cr &\quad \times \lbrack (q_{H}-q_{L}) (18cq_{H}^{3}-6\Theta q_{H}^{4}+2\Theta q_{L}^{4}-8\Theta q_{H}q_{L}^{3}\cr &\quad +8\Theta q_{H}^{3}q_{L}-3cq_{H}q_{L}^{2}+5cq_{H}^{2}q_{L}+4\Theta q_{H}^{2}q_{L}^{2})\cr &\quad +sq_{L}\lpar 4q_{H}-q_{L}\rpar (2\Theta q_{H}^{2}-3\Theta q_{H}q_{L}-cq_{H}+\Theta q_{L}^{2})].}$$
$$\eqalign{\overline{e}^{\gamma H} &= {1 \over q_{L}\lpar 3q_{H}-q_{L}\rpar (q_{H}-q_{L}) \lpar 5q_{H}-q_{L}\rpar } \cr &\quad \times \lbrack (q_{H}-q_{L}) (18cq_{H}^{3}-6\Theta q_{H}^{4}+2\Theta q_{L}^{4}-8\Theta q_{H}q_{L}^{3}\cr &\quad +8\Theta q_{H}^{3}q_{L}-3cq_{H}q_{L}^{2}+5cq_{H}^{2}q_{L}+4\Theta q_{H}^{2}q_{L}^{2})\cr &\quad +sq_{L}\lpar 4q_{H}-q_{L}\rpar (2\Theta q_{H}^{2}-3\Theta q_{H}q_{L}-cq_{H}+\Theta q_{L}^{2})].}$$
If
![]() $\overline{\gamma }^{H} = {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar q_{L}-2q_{H}\rpar \lpar q_{L}-q_{H}\rpar }$
,
$\overline{\gamma }^{H} = {2cq_{H}+\Theta (q_{H}-q_{L}) q_{L} \over \lpar q_{L}-2q_{H}\rpar \lpar q_{L}-q_{H}\rpar }$
,
![]() $\gamma ^{\ast H} \lt \overline{\gamma}^{H} \iff e \lt \overline{e}^{\gamma H^{\prime}},$
where:
$\gamma ^{\ast H} \lt \overline{\gamma}^{H} \iff e \lt \overline{e}^{\gamma H^{\prime}},$
where:
 $$\eqalign{\overline{e}^{\gamma H^{\prime }} &= {1 \over (q_{H}-q_{L}) \lpar 2q_{H}-q_{L}\rpar \lpar 3q_{H}-q_{L}\rpar }\cr &\quad \times \lbrack (q_{H}-q_{L}) (13cq_{H}^{2}-\Theta q_{H}^{3}-3cq_{H}q_{L}\cr &\quad +2\Theta q_{L}^{3}-10\Theta q_{H}q_{L}^{2}+9\Theta q_{H}^{2}q_{L}) \cr &\quad +s\lpar 4q_{H}-q_{L}\rpar (\Theta q_{L}^{2}-\Theta q_{H}q_{L}-2cq_{H})].}$$
$$\eqalign{\overline{e}^{\gamma H^{\prime }} &= {1 \over (q_{H}-q_{L}) \lpar 2q_{H}-q_{L}\rpar \lpar 3q_{H}-q_{L}\rpar }\cr &\quad \times \lbrack (q_{H}-q_{L}) (13cq_{H}^{2}-\Theta q_{H}^{3}-3cq_{H}q_{L}\cr &\quad +2\Theta q_{L}^{3}-10\Theta q_{H}q_{L}^{2}+9\Theta q_{H}^{2}q_{L}) \cr &\quad +s\lpar 4q_{H}-q_{L}\rpar (\Theta q_{L}^{2}-\Theta q_{H}q_{L}-2cq_{H})].}$$
Proof of Lemma 7
We focus on the case in which:
Moreover, we have to guarantee that at these equilibrium prices both firms are active in the market, i.e.,
![]() $0 \lt \theta_{L}^{\ast \ast H} \lt \theta_{H}^{\ast \ast H} \lt \Theta $
:
$0 \lt \theta_{L}^{\ast \ast H} \lt \theta_{H}^{\ast \ast H} \lt \Theta $
:
 $$\eqalign{\theta _{L}^{\ast \ast H} &= {q_{L}\Theta (q_{H} - q_{L}) + tq_{L} + 2cq_{H} \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0, \hbox{always;} \cr \theta_{H}^{\ast \ast H} - \theta_{L}^{\ast \ast H} &\gt 0\iff t \gt {c \lpar 2q_{H} - q_{L} \rpar - \Theta q_{L} (q_{H} - q_{L}) \over q_{L}} \equiv \underline{t}^{H}; \cr \theta_{H}^{\ast \ast H} - \Theta &\lt 0\iff t \lt {q_{H} [2\Theta (q_{H} - q_{L}) + c] \over \lpar 2q_{H} - q_{L} \rpar } \equiv \overline{t}^{H}.}$$
$$\eqalign{\theta _{L}^{\ast \ast H} &= {q_{L}\Theta (q_{H} - q_{L}) + tq_{L} + 2cq_{H} \over \lpar 4q_{H} - q_{L} \rpar q_{L}} \gt 0, \hbox{always;} \cr \theta_{H}^{\ast \ast H} - \theta_{L}^{\ast \ast H} &\gt 0\iff t \gt {c \lpar 2q_{H} - q_{L} \rpar - \Theta q_{L} (q_{H} - q_{L}) \over q_{L}} \equiv \underline{t}^{H}; \cr \theta_{H}^{\ast \ast H} - \Theta &\lt 0\iff t \lt {q_{H} [2\Theta (q_{H} - q_{L}) + c] \over \lpar 2q_{H} - q_{L} \rpar } \equiv \overline{t}^{H}.}$$
This also verifies that
![]() $p_{H}^{\ast \ast H} \gt t$
and
$p_{H}^{\ast \ast H} \gt t$
and
![]() $p_{L}^{\ast \ast H} \gt c$
, as it can be easily ascertained. In addition,
$p_{L}^{\ast \ast H} \gt c$
, as it can be easily ascertained. In addition,
![]() $\underline{t}^{H} \gt \widetilde{t}$
holds, and then p
H
>p
L
when
$\underline{t}^{H} \gt \widetilde{t}$
holds, and then p
H
>p
L
when
![]() $\theta_{H} \gt \theta_{L}$
. Moreover,
$\theta_{H} \gt \theta_{L}$
. Moreover,
![]() $\underline{t}^{H} \lt 0$
iff
$\underline{t}^{H} \lt 0$
iff
![]() $\Theta \gt \underline{\Theta}^{H}$
. Hence, it is convenient to assume again that
$\Theta \gt \underline{\Theta}^{H}$
. Hence, it is convenient to assume again that
![]() $\Theta \gt \underline{\Theta}^{H}$
in order to eliminate the condition
$\Theta \gt \underline{\Theta}^{H}$
in order to eliminate the condition
![]() $t \gt \underline{t}^{H}$
. This reduces the number of cases to be examined, without losing economic intuition. By combining the previous conditions, it follows that conditions
$t \gt \underline{t}^{H}$
. This reduces the number of cases to be examined, without losing economic intuition. By combining the previous conditions, it follows that conditions
![]() $\Theta \gt \underline{\Theta}^{H}$
and
$\Theta \gt \underline{\Theta}^{H}$
and
![]() $t \lt \overline{t}^{H}$
are required to have both players active in an uncovered market.
$t \lt \overline{t}^{H}$
are required to have both players active in an uncovered market.
Proof of Lemma 8
From (10),
![]() $t^{\ast H}\ges 0$
iff
$t^{\ast H}\ges 0$
iff
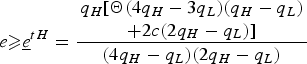 $e\ges \underline{e}^{tH} = {\matrix{q_{H} [\Theta (4q_{H} - 3q_{L}) (q_{H} - q_{L}) \cr + 2c(2q_{H} - q_{L})]} \over (4q_{H} - q_{L}) (2q_{H} - q_{L})}$
, while
$e\ges \underline{e}^{tH} = {\matrix{q_{H} [\Theta (4q_{H} - 3q_{L}) (q_{H} - q_{L}) \cr + 2c(2q_{H} - q_{L})]} \over (4q_{H} - q_{L}) (2q_{H} - q_{L})}$
, while
![]() $t^{\ast H} \lt \overline{t}^{H}$
iff
$t^{\ast H} \lt \overline{t}^{H}$
iff
![]() $e \lt \overline{e}^{tH} = {q_{H} \lsqb \Theta \lpar 4q_{H} - 3q_{L} \rpar (q_{H} - q_{L}) + c \lpar 3q_{H} - 2q_{L} \rpar \rsqb \over \lpar 2q_{H} - q_{L}\rpar ^{2}}$
.
$e \lt \overline{e}^{tH} = {q_{H} \lsqb \Theta \lpar 4q_{H} - 3q_{L} \rpar (q_{H} - q_{L}) + c \lpar 3q_{H} - 2q_{L} \rpar \rsqb \over \lpar 2q_{H} - q_{L}\rpar ^{2}}$
.
Proof of Proposition 2
This proof can be found in section 1 of the online appendix, together with the social welfare expressions that depend on the policy instrument adopted by the policy maker (see Remarks 3 and 4).


