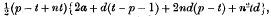Research Article
Coordinates, Conics and Conjugate Points
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 1-7
-
- Article
-
- You have access
- Export citation
A Limit Proof of the Theorem Euc. III, 35
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 7-8
-
- Article
-
- You have access
- Export citation
On Recurring Decimals
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 8-10
-
- Article
-
- You have access
- Export citation
Note on a trigonometrical proof of the orthocentre property of a triangle
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 11
-
- Article
-
- You have access
- Export citation
A Proof of the Addition Theorem in Trigonometry
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 12-13
-
- Article
-
- You have access
- Export citation
Series summable as Arithmetical Progressions
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 14-15
-
- Article
-
- You have access
- Export citation
Kepler's Law of Refraction
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 15-16
-
- Article
-
- You have access
- Export citation
Front matter
MAN volume 23 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation