Research Article
Whewell's Puzzle
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 135-136
-
- Article
-
- You have access
- Export citation
On the Solubility of Linear Algebraic Equations (Contd.)
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 137-138
-
- Article
-
- You have access
- Export citation
Proof of the sufficiency of the determinant condition for the consistency of a system of n homogeneous linear equations In n variables
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 139
-
- Article
-
- You have access
- Export citation
On the necessary and sufficient condition for the degeneracy of a quadratic function of a number of variables
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 140-141
-
- Article
-
- You have access
- Export citation
On the sufficiency of the condition for a limit
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 141-142
-
- Article
-
- You have access
- Export citation
Front matter
MAN volume 12 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation

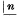 or
or