No CrossRef data available.
Article contents
A Note on Stirling's Theorem
Published online by Cambridge University Press: 31 October 2008
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Γ(1 + x) = √(2πx)xxe–x φ(x);
This result is Stirling's theorem. A simple proof is given in § 1.87 of Titchmarsh's Theory of Functions (Oxford Univ. Press, 1932).
Rather more than Stirling's theorem can be proved by a method which assumes nothing but the definition of the Γ-function, and Γ (½) = √π, from which it follows that
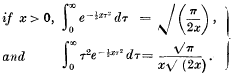
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1933
You have
Access