No CrossRef data available.
Article contents
A model of a hyperboloid of one sheet and its asymptotic cone
Published online by Cambridge University Press: 31 October 2008
Extract
In this article is described the construction of a thread model of a hyperboloid of one sheet (H) and its asymptotic cone (C). It ia simple to make, requiring only cardboard and thread, and can be made collapsible and of pocket size if desired. The model consists of two hinged pieces of cardboard (intersecting planes π and 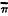 ) on which are drawn circles SH,
) on which are drawn circles SH,  respectively in which the planes meet H, and the concentric circles SC,
respectively in which the planes meet H, and the concentric circles SC, 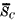 respectively in which the planes meet C. A number of generators of the same system on H are now represented by threads joining SH and
respectively in which the planes meet C. A number of generators of the same system on H are now represented by threads joining SH and  , and the corresponding parallel generators of C are represented by threads joining SC and
, and the corresponding parallel generators of C are represented by threads joining SC and 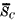 . In order to ensure that these generators are well spaced, those of C are taken at equal eccentric angles apart in a principal elliptic section. The main theorem used in the design is that if l a generator of C, then the tangent plane to C at points of l meets H in two generators both of which are parallel to l
. In order to ensure that these generators are well spaced, those of C are taken at equal eccentric angles apart in a principal elliptic section. The main theorem used in the design is that if l a generator of C, then the tangent plane to C at points of l meets H in two generators both of which are parallel to l
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1945
References
page note 23 1 The author's model (measuring 5″ by 4″ when closed) was shown at a meeting of the Edinburgh Mathematical Society, 2nd June, 1945, along with some other pocket quadrics also made by the author. For descriptions of the others (folding string models and collapsible models made from circular cardboard sections) see McCrea, W. H., Analytical geometry of three dimensions, University Mathematical Texts, Edinburgh (Oliver & Boyd), 1942, pp. 110–124Google Scholar; Turnbull, H. W., “Collapsible circular sections of quadric surfaces,” Edinburgh Math. Notes, No. 32, 1941, pp. xvi–xix.Google Scholar


