Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-05T22:53:06.334Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for solutions of linear differential equations a contribution to the theory of servomechanisms

Published online by Cambridge University Press:  31 October 2008

Hans Bückner
Hans Bückner
Affiliation:
Göttingen.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the nth order differential equation

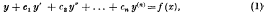
where the coefficients cv are real constants and f is a real function continuous in the interval a≦ x ≦ b. The following theorem will be proved in §4:

If the characteristic equation of (I) has no purely imaginary roots, then a particular integral η (x) can always be found which satisfies the inequality

where C is a certain function of the cv only and M is the maximum of |f|. In particular we may take C = 1 if all roots of the characteristic equation are real.

Type
Research Article
Information
Edinburgh Mathematical Notes , Volume 38 , January 1952 , pp. 13 - 16
Copyright
Copyright © Edinburgh Mathematical Society 1952

References

1 The author has previously shown that the result is true, more generally, if c 1 is a continuous non-vanishing function of x: see Zeitschrift für angewandte Mathematik und Mechanik, 38 (1942), 143–152 (Hilfssate, 144).Google Scholar

1 Only trivial modifications are required if the roots are all real or all unreal.