Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T18:27:20.907Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO-STEP ESTIMATION OF QUANTILE PANEL DATA MODELS WITH INTERACTIVE FIXED EFFECTS

Published online by Cambridge University Press:  18 August 2022

Liang Chen
Liang Chen*
Affiliation:
Peking University HSBC Business School
*
Address correspondence to Liang Chen, Peking University HSBC Business School, No. 2199 Lishui Road, Shenzhen, Guangdong 518055, China; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper considers the estimation of panel data models with interactive fixed effects where the idiosyncratic errors are subject to conditional quantile restrictions. An easy-to-implement two-step estimator is proposed for the coefficients of the observed regressors. In the first step, the principal component analysis is applied to the cross-sectional averages of the regressors to estimate the latent factors. In the second step, the smoothed quantile regression is used to estimate the coefficients of the observed regressors and the factor loadings jointly. The consistency and asymptotic normality of the estimator are established under large 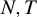$N,T$ asymptotics. It is found that the asymptotic distribution of the estimator suffers from asymptotic biases, and this paper shows how to correct the biases using both analytical and split-panel jackknife bias corrections. Simulation studies confirm that the proposed estimator performs well with moderate sample sizes.

Type
ARTICLES
Information
Econometric Theory , Volume 40 , Issue 2 , April 2024 , pp. 419 - 446
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

I am indebted to Liangjun Su and three anonymous referees for their constructive inputs which have greatly improved the paper. Financial support from the National Natural Science Foundation of China (Grant No. 71703089) is gratefully acknowledged.

References

REFERENCES

Abrevaya, J. & Dahl, C.M. (2008) The effects of birth inputs on birthweight: Evidence from quantile estimation on panel data. Journal of Business & Economic Statistics 26(4), 379–397.CrossRefGoogle Scholar
Ahn, S.C. & Horenstein, A.R. (2013) Eigenvalue ratio test for the number of factors. Econometrica 81(3), 1203–1227.Google Scholar
Amemiya, T. (1982) Two stage least absolute deviations estimators. Econometrica 50(3), 689–711.CrossRefGoogle Scholar
Ando, T. & Bai, J. (2020) Quantile co-movement in financial markets: A panel quantile model with unobserved heterogeneity. Journal of the American Statistical Association 115(529), 266–279.CrossRefGoogle Scholar
Arellano, M. & Bonhomme, S. (2016) Nonlinear panel data estimation via quantile regressions. The Econometrics Journal 19(3), C61–C94.CrossRefGoogle Scholar
Bai, J. (2003) Inferential theory for factor models of large dimensions. Econometrica 71(1), 135–171.CrossRefGoogle Scholar
Bai, J. (2009) Panel data models with interactive fixed effects. Econometrica 77(4), 1229–1279.Google Scholar
Bai, J. & Ng, S. (2002) Determining the number of factors in approximate factor models. Econometrica 70(1), 191–221.CrossRefGoogle Scholar
Belloni, A., Chen, M., & Padilla, O.H.M. (2019) High Dimensional Latent Panel Quantile Regression with an Application to Asset Pricing. WERPS working paper 1230, Department of Economics, University of Warwick.Google Scholar
Cai, Z., Chen, L., & Fang, Y. (2018) A semiparametric quantile panel data model with an application to estimating the growth effect of FDI. Journal of Econometrics 206(2), 531–553.CrossRefGoogle Scholar
Canay, I.A. (2011) A simple approach to quantile regression for panel data. The Econometrics Journal 14(3), 368–386.CrossRefGoogle Scholar
Chen, L. (2015) Set identification of panel data models with interactive effects via quantile restrictions. Economics Letters 137, 36–40.CrossRefGoogle Scholar
Chen, L. (2019) Nonparametric Quantile Regressions for Panel Data Models with Large T. PHBS working paper 20210104, Peking University HSBC Business School.Google Scholar
Chen, L., Dolado, J.J., & Gonzalo, J. (2021a) Quantile factor models. Econometrica 89(2), 875–910.CrossRefGoogle Scholar
Chen, L. & Huo, Y. (2021) A simple estimator for quantile panel data models using smoothed quantile regressions. The Econometrics Journal 24(2), 247–263.CrossRefGoogle Scholar
Chen, M. (2016) Estimation of Nonlinear Panel Models with Multiple Unobserved Effects. WERPS Working paper 1120, Department of Economics, University of Warwick.Google Scholar
Chen, M., Fernández-Val, I., & Weidner, M. (2021b) Nonlinear factor models for network and panel data. Journal of Econometrics 220(2), 296–324.CrossRefGoogle Scholar
Chudik, A. & Pesaran, H. (2015) Large panel data models with cross-sectional dependence. In Baltagi, B. H. (ed.), The Oxford Handbook of Panel Data , pp. 3–45, Oxford University Press.CrossRefGoogle Scholar
Dhaene, G. & Jochmans, K. (2015) Split-panel jackknife estimation of fixed-effect models. The Review of Economic Studies 82(3), 991–1030.CrossRefGoogle Scholar
Feng, J. (2019) Regularized Quantile Regression with Interactive Fixed Effects. arXiv:1911.00166 Google Scholar
Fernández-Val, I. & Weidner, M. (2016) Individual and time effects in nonlinear panel models with large N, T . Journal of Econometrics 192(1), 291–312.CrossRefGoogle Scholar
Galvao, A.F. (2011) Quantile regression for dynamic panel data with fixed effects. Journal of Econometrics 164(1), 142–157.CrossRefGoogle Scholar
Galvao, A.F., Gu, J., & Volgushev, S. (2020) On the unbiased asymptotic normality of quantile regression with fixed effects. Journal of Econometrics 218(1), 178–215.CrossRefGoogle Scholar
Galvao, A.F. & Kato, K. (2016) Smoothed quantile regression for panel data. Journal of Econometrics 193(1), 92–112.CrossRefGoogle Scholar
Galvao, A.F., Lamarche, C., & Lima, L.R. (2013) Estimation of censored quantile regression for panel data with fixed effects. Journal of the American Statistical Association 108(503), 1075–1089.Google Scholar
Galvao, A.F. & Montes-Rojas, G.V. (2010) Penalized quantile regression for dynamic panel data. Journal of Statistical Planning and Inference 140(11), 3476–3497.Google Scholar
Graham, B.S., Hahn, J., Poirier, A., & Powell, J.L. (2018) A quantile correlated random coefficients panel data model. Journal of Econometrics 206(2), 305–335.CrossRefGoogle Scholar
Hahn, J. & Kuersteiner, G. (2011) Bias reduction for dynamic nonlinear panel models with fixed effects. Econometric Theory 27(6), 1152–1191.CrossRefGoogle Scholar
Harding, M. & Lamarche, C. (2014) Estimating and testing a quantile regression model with interactive effects. Journal of Econometrics 178, 101–113.CrossRefGoogle Scholar
Harding, M., Lamarche, C., & Pesaran, M.H. (2020) Common correlated effects estimation of heterogeneous dynamic panel quantile regression models. Journal of Applied Econometrics 35(3), 294–314.Google Scholar
Horowitz, J.L. (1998) Bootstrap methods for median regression models. Econometrica , 1327–1351.CrossRefGoogle Scholar
Karabiyik, H., Reese, S., & Westerlund, J. (2017) On the role of the rank condition in CCE estimation of factor-augmented panel regressions. Journal of Econometrics 197(1), 60–64.CrossRefGoogle Scholar
Kato, K., Galvao, A.F., & Montes-Rojas, G.V. (2012) Asymptotics for panel quantile regression models with individual effects. Journal of Econometrics 170(1), 76–91.CrossRefGoogle Scholar
Koenker, R. (2004) Quantile regression for longitudinal data. Journal of Multivariate Analysis 91(1), 74–89.CrossRefGoogle Scholar
Lamarche, C. (2010) Robust penalized quantile regression estimation for panel data. Journal of Econometrics 157(2), 396–408.CrossRefGoogle Scholar
Lu, X. & Su, L. (2016) Shrinkage estimation of dynamic panel data models with interactive fixed effects. Journal of Econometrics 190(1), 148–175.CrossRefGoogle Scholar
Ma, S., Linton, O., & Gao, J. (2021) Estimation and inference in semiparametric quantile factor models. Journal of Econometrics 222(1), 295–323.CrossRefGoogle Scholar
Moon, H.R. & Weidner, M. (2015) Linear regression for panel with unknown number of factors as interactive fixed effects. Econometrica 83(4), 1543–1579.CrossRefGoogle Scholar
Muller, H.G. (1984) Smooth optimum kernel estimators of densities, regression curves and modes. Annals of Statistics 12(2), 766–774.CrossRefGoogle Scholar
Pesaran, M.H. (2006) Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74(4), 967–1012.CrossRefGoogle Scholar
Rao, B.P. (2009) Conditional independence, conditional mixing and conditional association. Annals of the Institute of Statistical Mathematics 61(2), 441–460.Google Scholar
Rosen, A.M. (2012) Set identification via quantile restrictions in short panels. Journal of Econometrics 166(1), 127–137.CrossRefGoogle Scholar
Su, L. & Chen, Q. (2013) Testing homogeneity in panel data models with interactive fixed effects. Econometric Theory 29(6), 1079–1135.CrossRefGoogle Scholar
Yoon, J. & Galvao, A.F. (2020) Cluster robust covariance matrix estimation in panel quantile regression with individual fixed effects. Quantitative Economics 11(2), 579–608.Google Scholar
Supplementary material: PDF

Chen supplementary material

Online Appendix

Download Chen supplementary material(PDF)
PDF 536.5 KB