Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T08:14:34.607Z Has data issue: false hasContentIssue false
  • English
  • Français

TARGETING ESTIMATION OF CCC-GARCH MODELS WITH INFINITE FOURTH MOMENTS

Published online by Cambridge University Press:  07 September 2015

Rasmus Søndergaard Pedersen
Rasmus Søndergaard Pedersen*
Affiliation:
University of Copenhagen
*
*Address correspondence to Rasmus Søndergaard Pedersen, University of Copenhagen, Department of Economics, Oester Farimagsgade 5, Building 26, 1353 Copenhagen K, Denmark. e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

As an alternative to quasi-maximum likelihood, targeting estimation is a much applied estimation method for univariate and multivariate GARCH models. In terms of variance targeting estimation, recent research has pointed out that at least finite fourth moments of the data generating process is required, if one wants to perform inference in GARCH models by relying on asymptotic normality of the estimator. Such moment conditions may not be satisfied in practice for financial returns, highlighting a potential drawback of variance targeting estimation. In this paper, we consider the large-sample properties of the variance targeting estimator for the multivariate extended constant conditional correlation GARCH model when the distribution of the data generating process has infinite fourth moments. Using nonstandard limit theory, we derive new results for the estimator stating that, under suitable conditions, its limiting distribution is multivariate stable. The rate of consistency of the estimator is slower than 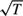$\sqrt T$ and depends on the tail shape of the data generating process. A simulation study illustrates the derived properties of the targeting estimator.

Type
ARTICLES
Information
Econometric Theory , Volume 32 , Issue 2 , April 2016 , pp. 498 - 531
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

von Bahr, B. & Esseen, C.-G. (1965) Inequalities for the rth absolute moment of a sum of random variables, 1 ≤ r ≤ 2. The Annals of Mathematical Statistics 36, 299–303.Google Scholar
Bartkiewicz, K., Jakubowski, A., Mikosch, T., & Wintenberger, O. (2011) Stable limits for sums of dependent infinite variance random variables. Probability Theory and Related Fields 150, 337–372.Google Scholar
Basrak, B., Davis, R.A., & Mikosch, T. (2002a) A characterization of multivariate regular variation. The Annals of Applied Probability 12, 908–920.Google Scholar
Basrak, B., Davis, R.A., & Mikosch, T. (2002b) Regular variation of GARCH processes. Stochastic Processes and their Applications 99, 95–115.Google Scholar
Basrak, B. & Segers, J. (2009) Regularly varying multivariate time series. Stochastic Processes and their Applications 119, 1055–1080.Google Scholar
Bauwens, L., Laurent, S., & Rombouts, J.V.K. (2006) Multivariate GARCH models: A survey. Journal of Applied Econometrics 21, 79–109.CrossRefGoogle Scholar
Berkes, I. & Horváth, L. (2003) The rate of consistency of the quasi-maximum likelihood estimator. Statistics & Probability Letters 61, 133–143.Google Scholar
Berkes, I. & Horváth, L. (2004) The efficiency of the estimators of the parameters in GARCH processes. The Annals of Statistics 32, 633–655.Google Scholar
Berkes, I., Horváth, L., & Kokoszka, P. (2003) Estimation of the maximal moment exponent of a GARCH(1,1) sequence. Econometric Theory 19, 565–586.Google Scholar
Berkes, I., Horváth, L., & Schauer, J. (2010) Non-central limit theorems for random selections. Probability Theory and Related Fields 147, 449–479.Google Scholar
Billingsley, P. (1999) Convergence of Probability Measures, 2nd ed, Wiley.Google Scholar
Bingham, N., Goldie, C., & Teugels, J. (1987) Regular Variation, Encyclopedia of Mathematics and its Applications, Cambridge University Press.Google Scholar
Bollerslev, T. (1990) Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. The Review of Economics and Statistics 72, 498–505.Google Scholar
Boman, J. & Lindskog, F. (2009) Support theorems for the Radon transform and Cramér-Wold theorems. Journal of Theoretical Probability 22, 683–710.Google Scholar
Bougerol, P. & Picard, N. (1992) Strict stationarity of generalized autoregressive processes. The Annals of Probability 20, 1714–1730.Google Scholar
Boussama, F. (1998) Ergodité, mélange et estimation dans les modèles GARCH, Ph.D. thesis, Université Paris 7.Google Scholar
Boussama, F., Fuchs, F., & Stelzer, R. (2011) Stationarity and geometric ergodicity of BEKK multivariate GARCH models. Stochastic Processes and their Applications 121, 2331–2360.Google Scholar
Davis, R.A. & Hsing, T. (1995) Point process and partial sum convergence for weakly dependent random variables with infinite variance. The Annals of Probability 23, 879–917.Google Scholar
Davis, R.A. & Mikosch, T. (1998) The sample autocorrelations of heavy-tailed processes with applications to ARCH. The Annals of Statistics 26, 2049–2080.Google Scholar
Engle, R. & Mezrich, J. (1996) GARCH for groups. Risk Magazine 9, 36–40.Google Scholar
Escanciano, J.C. (2009) Quasi-maximum likelihood estimation of semi-strong GARCH models. Econometric Theory 25, 561–570.Google Scholar
Fernández, B. & Muriel, N. (2009) Regular variation and related results for the multivariate GARCH(p,q) model with constant conditional correlations. Journal of Multivariate Analysis 100, 1538–1550.Google Scholar
Francq, C., Horváth, L., & Zakoïan, J.-M. (2011) Merits and drawbacks of variance targeting in GARCH models. Journal of Financial Econometrics 9, 619–656.CrossRefGoogle Scholar
Francq, C., Horváth, L., & Zakoïan, J.-M. (2014) Variance targeting estimation of multivariate GARCH models. Journal of Financial Econometrics, to appear.Google Scholar
Francq, C. & Zakoïan, J.-M. (2010) GARCH Models: Structure, Statistical Inference and Financial Applications, Wiley.Google Scholar
Francq, C. & Zakoïan, J.-M. (2012) QML estimation of a class of multivariate asymmetric GARCH models. Econometric Theory 28, 179–206.Google Scholar
Hafner, C.M. & Preminger, A. (2009) On asymptotic theory for multivariate GARCH models. Journal of Multivariate Analysis 100, 2044–2054.Google Scholar
Hall, P. & Yao, Q. (2003) Inference in ARCH and GARCH models with heavy-tailed errors. Econometrica 71, 285–317.CrossRefGoogle Scholar
He, C. & Teräsvirta, T. (2004) An extended constant conditional correlation GARCH model and its fourth-moment structure. Econometric Theory 20, 904–926.Google Scholar
Hill, J.B. & Renault, E. (2012) Variance targeting for heavy tailed time series, Unpublished manuscript, University of North Carolina at Chapel Hill.Google Scholar
Jeantheau, T. (1998) Strong consistency of estimators for multivariate ARCH models. Econometric Theory 14, 70–86.Google Scholar
Kesten, H. (1973) Random difference equations and Renewal theory for products of random matrices. Acta Mathematica 131, 207–248.Google Scholar
Kristensen, D. & Linton, O. (2004) Consistent standard errors for target variance approach to GARCH estimation. Econometric Theory 20, 990–993.Google Scholar
Ling, S. & McAleer, M. (2003) Asymptotic theory for a vector ARMA-GARCH model. Econometric Theory 19, 280–310.Google Scholar
Loretan, M. & Phillips, P.C.B. (1994) Testing the covariance stationarity of heavy-tailed time series: An overview of the theory with applications to several financial datasets. Journal of Empirical Finance 1, 211–248.CrossRefGoogle Scholar
Meitz, M. & Saikkonen, P. (2008) Ergodicity, mixing, and existence of moments of a class of Markov models with applications to GARCH and ACD models. Econometric Theory 24, 1291–1320.Google Scholar
Mikosch, T. (2004) Modeling dependence and tails of financial time series, In Finkenstädt, B. & Rootzén, H. (eds.), Extreme Values in Finance, Telecommunications, and the Environment, Chapman & Hall/CRC, Monographs on Statistics and Applied Probability, vol. 99, chap. 5, 185–286.Google Scholar
Mikosch, T. & Straumann, D. (2006) Stable limits of martingale transforms with application to the estimation of GARCH parameters. The Annals of Statistics 34, 493–522.Google Scholar
Pedersen, R.S. & Rahbek, A. (2014) Multivariate variance targeting in the BEKK-GARCH model. The Econometrics Journal 17, 24–55.Google Scholar
Resnick, S.I. (1986) Point processes, regular variation and weak convergence. Advances in Applied Probability 18, 66–138.Google Scholar
Resnick, S.I. (1987) Extreme Values, Regular Variation, and Point Processes, Applied Probability, Springer-Verlag.CrossRefGoogle Scholar
Resnick, S.I. (2007) Heavy-Tail Phenomena: Probabilistic and Statistical Modeling, Springer Series in Operations Research, Springer.Google Scholar
Samorodnitsky, G. & Taqqu, M. (1994) Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance, Stochastic modeling, Chapman & Hall.Google Scholar
Stărică, C. (1999) Multivariate extremes for models with constant conditional correlations. Journal of Empirical Finance 6, 515–553.Google Scholar
Tjøstheim, D. (1990) Non-linear time series and Markov chains. Advances in Applied Probability 22, 587–611.Google Scholar
Trapani, L. (2014) Testing for (in)finite moments, Working paper 19, Cass Business School, Faculty of Finance.Google Scholar
Vaynman, I. & Beare, B.K. (2014) Stable limit theory for the variance targeting estimator, In Chang, Y., Fomby, T.B., & Park, J.Y. (eds.), Essays in Honor of Peter C. B. Phillips, Emerald Group Publishing Limited, Advances in Econometrics, vol. 33, chap. 24, 639–672.Google Scholar