Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T18:10:35.807Z Has data issue: false hasContentIssue false
  • English
  • Français

STATISTICAL INFERENCE WITH F-STATISTICS WHEN FITTING SIMPLE MODELS TO HIGH-DIMENSIONAL DATA

Published online by Cambridge University Press:  27 September 2021

Hannes Leeb  and
Lukas Steinberger
Hannes Leeb*
Affiliation:
University of Vienna
Lukas Steinberger
Affiliation:
University of Vienna
*
Address correspondence to Hannes Leeb, Department of Statistics, University of Vienna, Oskar-Morgenstern-Platz 1, 1090 Vienna, Austria; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study linear subset regression in the context of the high-dimensional overall model 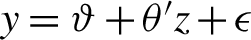$y = \vartheta +\theta ' z + \epsilon $ with univariate response y and a d-vector of random regressors z, independent of 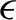$\epsilon $. Here, “high-dimensional” means that the number d of available explanatory variables is much larger than the number n of observations. We consider simple linear submodels where y is regressed on a set of p regressors given by 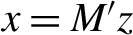$x = M'z$, for some $d \times p$ matrix M of full rank $p < n$. The corresponding simple model, that is, 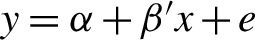$y=\alpha +\beta ' x + e$, is usually justified by imposing appropriate restrictions on the unknown parameter 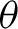$\theta $ in the overall model; otherwise, this simple model can be grossly misspecified in the sense that relevant variables may have been omitted. In this paper, we establish asymptotic validity of the standard F-test on the surrogate parameter 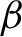$\beta $, in an appropriate sense, even when the simple model is misspecified, that is, without any restrictions on 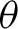$\theta $ whatsoever and without assuming Gaussian data.

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 6: SPECIAL ISSUE IN HONOR OF BENEDIKT M PÖTSCHER , December 2023 , pp. 1249 - 1272
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (https://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

The first author’s research was partially supported by FWF projects P 26354-N26 and P 28233-N32.

References

REFERENCES

Abadie, G., Imbens, G. W. & Zheng, F. (2014) Inference for misspecified models with fixed regressors. Journal of the American Statistical Association 109, 1601–1614.CrossRefGoogle Scholar
Akritas, M. & Arnold, S. (2000) Asymptotics for analyis of variance when the number of levels is large. Journal of the American Statistical Association 95, 212–226.CrossRefGoogle Scholar
Anderson, T. W. (1958) An Introduction to Multivariate Analysis. Wiley.Google Scholar
Bachoc, F., Leeb, H. & Pötscher, B. M. (2019) Valid confidence intervals for post-model-selection predictors. Annals of Statistics 47, 1475–1504.CrossRefGoogle Scholar
Bai, Z. & Saranadasa, H. (1996) Effect of high dimension: By an example of a two sample problem. Statistica Sinica 6, 311–329.Google Scholar
Baik, J. & Silverstein, J. W. (2006) Eigenvalues of large sample covariance matrices of spiked population models. Journal of Multivariate Analysis 97, 1382–1408.CrossRefGoogle Scholar
Bathke, A. & Lankowski, D. (2005) Rank procedures for a large number of treatments. Journal of Statistical Planning and Inference 133, 223–238.CrossRefGoogle Scholar
Boos, D. D. & Brownie, C. (1995) ANOVA and rank tests when the number of treatments is large. Statistics and Probability Letters 23, 183–191.CrossRefGoogle Scholar
Boos, D.D. & Stefanski, L.A. (2013) Essential Statistical Inference, Springer Texts in Statistics. Springer.CrossRefGoogle Scholar
Brannath, W. & Scharpenberg, M. (2014) Interpretation of linear regression coefficients under mean model miss-specification. arXiv:1409.8544.Google Scholar
Buja, A.R., Brown, L. D., George, E., Pitkin, E., Traskin, M., Zhan, K., & Zhao, L. (2014) A conspiracy of random predictors and model violations against classical inference in regression. arXiv:1404.1578.Google Scholar
Cai, T., Ma, Z. & Wu, Y. (2013) Optimal estimation and rank detection for sparse spiked covariance matrices. Probability Theory and Related Fields 161, 1–35.Google Scholar
Cattaneo, M. D., Jansson, M. & Newey, W. K. (2018) Inference in linear regression models with many covariates and heteroscedasticity. Journal of the American Statistical Association 113, 1350–1361.CrossRefGoogle Scholar
Chen, S.-X. & Qin, Y.-L. (2010) A two-sample test for high-dimensional data with applications to gene-set testing. Annals of Statistics 38, 808–835.CrossRefGoogle Scholar
Choi, H. S. & Kiefer, N. M. (2011) Geometry of the log-likelihood ratio statistic in misspecified models. Journal of Statistical Planning and Inference 141, 2091–2099.CrossRefGoogle Scholar
Dobriban, E. & Su, W. (2018) Robust inference under heteroskedasticity via the Hadamard estimator. arXiv:1807.00347.Google Scholar
Donoho, D. L., Gavish, M. & Johnstone, I. M. (2018) Optimal shrinkage of eigenvalues in the spiked covariance model. Annals of Statistics 46, 1742–1778.CrossRefGoogle ScholarPubMed
Eicker, F. (1967) Limit theorems for regressions with unequal and dependent errors. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, pp. 59–82. University of California Press.Google Scholar
Fomby, T.B. & Hill, R.C. (2003) Maximum Likelihood Estimation of Misspecified Models: Twenty Years Later, Advances in Econometrics, 17. Elsevier.CrossRefGoogle Scholar
Hall, P. & Li, K.-C. (1993) On almost linearity of low dimensional projections from high dimensional data. Annals of Statistics 21, 867–889.CrossRefGoogle Scholar
Harrar, S. & Bathke, A. C. (2008) Nonparametric methods for unbalanced multivariate data and many factor levels. Journal of Multivariate Analysis 99, 1635–1664.CrossRefGoogle Scholar
Huber, P. J. (1967) The behavior of maximum likelihood estimates under nonstandard conditions. In Le Cam, Lucien M., Neyman, Jerzy (eds.), Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, pp. 221–233. University of California Press.Google Scholar
Jensen, D. R. & Ramirez, D. E. (1991) Misspecified ${t}^2$ tests. I. Location and scale. Communications in Statistics. Theory and Methods 20, 249–259.CrossRefGoogle Scholar
Jochmans, K. Heteroscedasticity-robust inference in linear regression models with many covariates. Journal of the American Statistical Association, first published online 19 November 2020. https://doi.org/10.1080/01621459.2020.1831924.Google Scholar
Johnstone, I. M. (2001) On the distribution of the largest eigenvalue in principal components analysis. Annals of Statistics 29, 295–327.CrossRefGoogle Scholar
Leeb, H. (2013) On the conditional distributions of low-dimensional projections from high-dimensional data. Annals of Statistics 41, 464–483.CrossRefGoogle Scholar
Li, Z. & Yao, J. (2019) Testing for heteroscedasticity in high-dimensional regressions. Econometrics and Statistics 9, 122–139.CrossRefGoogle Scholar
Portnoy, S. (1984) Asymptotic behavior of $m$ -estimators of $p$ regression parameters when ${p}^2/ n$ is large. I. Consistency. Annals of Statististics 12, 1298–1309.Google Scholar
Portnoy, S. (1985) Asymptotic behavior of $m$ -estimators of $p$ regression parameters when ${p}^2/ n$ is large. II. Normal approximation. Annals of Statistics 13, 1403–1417.CrossRefGoogle Scholar
Preinerstorfer, D. & Pötscher, B. M. (2016) On size and power of heteroskedasticity and autocorrelation robust tests. Econometric Theory 32, 261–358.CrossRefGoogle Scholar
Ramirez, D. E. & Jensen, D. R. (1991) Misspecified ${t}^2$ tests. II. Series expansions. Communications in Statistics. Theory and Methods 20, 97–108.Google Scholar
Rosenthal, H. P. (1970) On the subspaces of ${L}^p\left(p>2\right)$ , spanned by sequences of independent random variables. Israel Journal of Mathematics 8, 273–303.CrossRefGoogle Scholar
Souders, T. M. & Stenbakken, G. N. (1991) Cutting the high cost of testing. IEEE Spectrum 28, 48–51.CrossRefGoogle Scholar
Steinberger, L. (2015) Statistical inference in high-dimensional linear regression based on simple working models. PhD thesis, University of Vienna.Google Scholar
Steinberger, L. (2016) The relative effects of dimensionality and multiplicity of hypotheses on the F-test in linear regression. Electronic Journal of Statistics 10, 2584–2640.CrossRefGoogle Scholar
Steinberger, L. & Leeb, H. (2018) On conditional moments of high-dimensional random vectors given lower-dimensional projections. Bernoulli 24, 565–591.CrossRefGoogle Scholar
Steinberger, L. & Leeb, H. (2019) Prediction when fitting simple models to high-dimensional data. Annals of Statistics 47, 1408–1442.CrossRefGoogle Scholar
Stock, J. H. & Watson, M. W. (2002) Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association 97, 1167–1179.CrossRefGoogle Scholar
van’t Veer, L. J., Dai, H., van de Vijver, M. J., He, Y. D., Hart, A. A. M., Mao, M., Peterse, H. L., van der Kooy, K., Marton, M. J., Witteveen, A. T., Schreiber, G. J., Kerkhoven, R. M., Roberts, C., Linsley, P. S., Bernards, R. & Friend, S. H. (2002) Gene expression profiling predicts clinical outcome of breast cancer. Nature 415, 530–536.CrossRefGoogle ScholarPubMed
Wang, S. & Cui, H. (2013) Generalized F test for high dimensional linear regression coefficients. Journal of Multivariate Analysis 117, 134–149.CrossRefGoogle Scholar
White, H. (1980a) A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 84, 817–838.CrossRefGoogle Scholar
White, H. (1980b) Using least squares to approximate unknown regression functions. International Economic Review 21, 149–170.CrossRefGoogle Scholar
Zhong, P. S. & Chen, S. X. (2011) Tests for high-dimensional regression coefficients with factorial designs. Journal of the American Statistical Association 106, 260–274.CrossRefGoogle Scholar