Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T18:20:56.220Z Has data issue: false hasContentIssue false
  • English
  • Français

SPECIFICATION TESTS FOR LATTICE PROCESSES

Published online by Cambridge University Press:  19 August 2014

Javier Hidalgo  and
Myung Hwan Seo
Javier Hidalgo
Affiliation:
London School of Economics and Seoul National University
Myung Hwan Seo*
Affiliation:
London School of Economics and Seoul National University
*
*Address correspondence to Myung Hwan Seo, London School of Economics, Houghton St., London WC2A 2AE, UK; e-mail: [email protected].; or to: Seoul National University, Kwan-Ak Gu, Seoul, Korea.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an omnibus test for the correct specification of the dynamics of a sequence 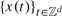$\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ in a lattice. As it happens with causal models and d = 1, its asymptotic distribution is not pivotal and depends on the estimator of the unknown parameters of the model under the null hypothesis. One first main goal of the paper is to provide a transformation to obtain an asymptotic distribution that is free of nuisance parameters. Secondly, we propose a bootstrap analog of the transformation and show its validity. Thirdly, we discuss the results when 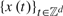$\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ are the errors of a parametric regression model. As a by product, we also discuss the asymptotic normality of the least squares estimator of the parameters of the regression model under very mild conditions. Finally, we present a small Monte Carlo experiment to shed some light on the finite sample behavior of our test.

Type
ARTICLES
Information
Econometric Theory , Volume 31 , Issue 2: Haavelmo Memorial Issue: Part Two , April 2015 , pp. 294 - 336
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baltagi, B., Kelejian, H.H., & Prucha, I.R. (eds.) (2007) Analysis of spatially dependent data. Annals issue. Journal of Econometrics, Annals Issue, 140.Google Scholar
Batchelor, L.I.A. & Reed, H.S. (1924) Relation of the variability of yields of fruit trees to the accuracy of field trials. Journal of Agricultural Research 12, 245–283.Google Scholar
Besag, J. (1974) Spatial interaction and the statistical analysis of lattice systems (with discussion). Journal of the Royal Statistical Society, Series B 36, 192–236.Google Scholar
Bickel, P.J. & Wichura, M.J. (1971) Convergence criteria for multiparameter stochastic processes and its applications. Annals of Mathematical Statistics 42, 1656–1670.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley.Google Scholar
Bloomfield, P. (1973) An exponential model for the spectrum of a scalar time series. Biometrika 61, 217–226.CrossRefGoogle Scholar
Bolthausen, E. (1982) On the central limit theorem for stationary mixing random fields. The Annals of Probability 10, 1047–1050.Google Scholar
Brillinger, D.R. (1981) Time Series, Data Analysis and Theory. Holden-Day.Google Scholar
Brown, R.L., Durbin, J., & Evans, J.M. (1975) Components of Cramér-von Mises statistics II. Journal of the Royal Statistical Society, Series B 37, 216–237.Google Scholar
Chen, H. & Romano, J.P. (1999) Bootstrap-assisted goodness-of-fit tests in the frequency domain. Journal of Time Series Analysis 20, 619–654.Google Scholar
Cressie, N.A.C. (1993) Statistics for Spatial Data. Wiley.Google Scholar
Cressie, N. & Huang, H.C. (1999) Classes of nonseparable, spatio-temporal stationary covariance functions. Journal of the American Statistical Association 94, 1330–1340.Google Scholar
Crujeiras, R.M., Fernandez-Casal, R., & Gonzalez-manteiga, W. (2008) An L 2-test for comparing spatial spectral densities. Statistics & Probability Letters 78, 2543–2551.Google Scholar
Dahlhaus, R. & Künsch, H. (1986) Edge effect and efficient parameter estimation for stationary random fields. Biometrika 74, 877–882.Google Scholar
Davis, R.A., Alexandre Trindade, A., & Breidt, F.J. (2001) Least absolute deviation estimation for all-pass time series models. Annals of Statistics 29, 919–946.Google Scholar
Delgado, M.A., Hidalgo, J., & Velasco, C. (2005) Distribution free goodness-of-fit tests for linear processes. Annals of Statistics 33, 2568–2609.Google Scholar
Delgado, M.A., Hidalgo, J., & Velasco, C. (2011) Bootstrap assisted specification tests for the Farima model. Econometric Theory 27, 1083–1116.Google Scholar
Eubank, R.L. & LaRicca, V. (1992) Asymptotic comparison of Cramér-von Mises and nonparametric techniques for testing goodness-of-fit. Annals of Statistics 20, 2071–2086.CrossRefGoogle Scholar
Fernandez-Casal, R., Gonzalez-Manteiga, W., & Febrero-Bande, M. (2003) Flexible spatio-temporal stationary variogram models. Statistics and Computing 13, 127–136.Google Scholar
Genton, M.G. & Koul, H.L. (2008) Minimum distance inference in unilateral autoregressive lattice processes. Statistica Sinica 18, 617–631.Google Scholar
Giacomini, R., Politis, D.N., & White, H. (2013) A warp-speed method for conducting Monte Carlo experiments involving bootstrap estimators. Econometric Theory 29, 567–609.Google Scholar
Grenander, U. (1950) Stochastic processes and statistical inference. Arkiv för Matematik 1, 195–277.Google Scholar
Guyon, X. (1982) Parameter estimation for a stationary process on a 𝑑-dimension lattice. Biometrika 69, 95–105.Google Scholar
Hainz, G. & Dahlhaus, R. (2000) Spectral domain bootstrap tests for stationary time series. Preprint.Google Scholar
Hannan, E.J. (1970) Multiple Time Series. Wiley.Google Scholar
Hannan, E.J. (1973) The asymptotic theory of linear time series models. Journal of Applied Probability 10, 130–145.Google Scholar
Hidalgo, J. (2009) Goodness of fit for lattice processes. Journal of Econometrics 151, 113–128.Google Scholar
Hidalgo, J. & Kreiss, J.P. (2006) Bootstrap specification tests for linear covariance stationary processes. Journal of Econometrics 133, 807–839.Google Scholar
Hong, Y. (1996) Consistent testing for serial-correlation of unknown form. Econometrica 64, 837–864.Google Scholar
Ibragimov, I.A. & Rozanov, Y.A. (1978) Gaussian Random Processes. Springer-Verlag.Google Scholar
Jenish, N. & Prucha, I.R. (2009) Central limit theorems and uniform laws of large numbers for arrays of random fields. Journal of Econometrics 150, 86–98.CrossRefGoogle ScholarPubMed
Khmaladze, E.V. (1981) Martingale approach in the theory of goodness-of-fit tests. Theory of Probability and Applications 26, 240–257.Google Scholar
Lanne, M. & Saikonnen, P. (2011) Noncausal autoregressive for economic time series. Journal of Time Series Econometrics 3, 1–30.Google Scholar
Lanne, M. & Saikonnen, P. (2013) Noncausal vector autoregression. Econometric Theory 29, 447–481.Google Scholar
Mardia, K.V. & Marshall, R.J. (1984) Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika 71, 135–146.Google Scholar
McKeague, I.W., Nikabadze, A.M., & Sun, Y. (1995) An omnibus test for independence of survival time from a covariate. Annals of Statistics 223, 450–475.Google Scholar
Mercer, W.B. & Hall, A.D. (1911) The experimental error of field trials. Journal of Agricultural Science 4, 107–132.Google Scholar
Mitchell, M.W., Genton, M.G., & Gumpertz, M.L. (2005) Testing for separability of space–time covariances. Environmetrics 16, 819–831.Google Scholar
Neyman, J. (1937) Smooth test for goodness of fit. Arkiv for matematik 20, 150–199.Google Scholar
Paparoditis, E. (2000) Spectral density based goodness-of-fit tests for time series models. Scandinavian Journal of Statistics 27, 143–176.Google Scholar
Robinson, P.M. (1988) The stochastic difference between econometric statistics. Econometrica 56, 531–548.Google Scholar
Robinson, P.M. (2012) Inference on power law spatial trends. Bernoulli 18, 644–677.Google Scholar
Robinson, P.M. & Thawornkaiwong, S. (2012) Statistical inference on regressing with spatial dependence. Journal of Econometrics 167, 521–542.Google Scholar
Robinson, P.M. & Vidal-Sanz, J. (2006) Modified Whittle estimation of multilateral models on a lattice. Journal of Multivariate Analysis 60, 234–349.Google Scholar
Schoenfeld, D.A. (1977) Asymptotic properties of tests based on linear combinations of the Cramér-von Mises statistic. Annals of Statistics 5, 1017–1026.Google Scholar
Shao, J. & Tu, D. (1995) The Jackknife and Bootstrap. Springer-Verlag.Google Scholar
Solo, V. (1986) Modeling of two-dimensional random field by parametric Cepstrum. IEEE Transactions on Information Theory 32, 743–750.Google Scholar
Stute, W. (1997) Nonparametric model checks for regression. Annals of Statistics 25, 613–641.Google Scholar
Whittle, P. (1954) On stationary processes in the plane. Biometrika 41, 434–449.Google Scholar
Yajima, Y. & Matsuda, Y. (2011) Asymptotic properties of the LSE of a spatial regression in both weakly and strongly dependent stationary random fields. Preprint. University of Tokyo.Google Scholar
Zhu, J., Huang, H.C., & Reyes, P.E. (2010) On selection of spatial linear models for lattice data. Journal of the Royal Statistical Society, Series B 72, 389–402.Google Scholar