Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T02:19:04.690Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMULTANEOUSLY MODELING CONDITIONAL HETEROSKEDASTICITY AND SCALE CHANGE

Published online by Cambridge University Press:  08 June 2004

Yuanhua Feng
Yuanhua Feng
Affiliation:
University of Konstanz
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes a semiparametric approach by introducing a smooth scale function into the standard generalized autoregressive conditional heteroskedastic (GARCH) model so that conditional heteroskedasticity (CH) and scale change in financial returns can be modeled simultaneously. An estimation procedure combining kernel estimation of the scale function and maximum likelihood estimation of the GARCH parameters is proposed. Asymptotic properties of the estimators are investigated in detail. 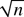It is shown that asymptotically normal, -consistent parameter estimation is available. A data-driven algorithm is developed for practical implementation. Finite sample performance of the proposal is studied through simulation. The proposal is applied to model CH and scale change in the daily S&P 500 and DAX 100 returns. It is shown that both series have simultaneously significant scale change and CH.We are very grateful to the co-editor and two referees for their helpful comments and suggestions, which led to a substantial improvement of this paper. The paper was finished under the advice of Professor Jan Beran, Department of Mathematics and Statistics, University of Konstanz, Germany, and was financially supported by the Center of Finance and Econometrics (CoFE), University of Konstanz. We thank colleagues in CoFE, especially Professor Winfried Pohlmeier, for their interesting questions at a talk of the author. It was these questions that motivated the author to write this paper. Our special thanks go to Dr. Erik Lüders, Department of Finance and Insurance, Laval University, and Stern School of Business, New York University, for his helpful suggestions.

Type
Research Article
Information
Econometric Theory , Volume 20 , Issue 3 , June 2004 , pp. 563 - 596
Copyright
© 2004 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Altman, N.S. (1990) Kernel smoothing with correlated errors. Journal of the American Statistical Association 85, 749–759.Google Scholar
Basrak, B., R.A. Davis, & T. Mikosch (2002) Regular variation of GARCH processes. Stochastic Processes and Their Applications 99, 95–115.Google Scholar
Beran, J. (1999) SEMIFAR Models: A Semiparametric Framework for Modelling Trends, Long Range Dependence, and Nonstationarity. CoFE discussion paper 99/16, University of Konstanz.
Beran, J. & Y. Feng (2001) Local polynomial estimation with a FARIMA-GARCH error process. Bernoulli 7, 733–750.Google Scholar
Beran, J. & Y. Feng (2002a) Local polynomial fitting with long-memory, short-memory and antipersistent errors. Annals of the Institute of Statistical Mathematics 54, 291–311.Google Scholar
Beran, J. & Y. Feng (2002b) Iterative plug-in algorithms for SEMIFAR models: Definition, convergence, and asymptotic properties. Journal of Computational and Graphical Statistics 11, 690–713.Google Scholar
Beran, J. & D. Ocker (2001) Volatility of stock market indices: An analysis based on SEMIFAR models. Journal of Business and Economic Statistic 19, 103–116.Google Scholar
Bollerslev, T. (1986) Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31, 307–327.Google Scholar
Brockwell, P.J. & R.A. Davis (1991) Time Series: Theory and Methods. Springer.
Dahlhaus, R. (1997) Fitting time series models to nonstationary processes. Annals of Statistics 25, 1–37.Google Scholar
Ding, Z., C.W.J. Granger, & R.F. Engle (1993) A long memory property of stock market returns and a new model. Journal of Empirical Finance 1, 83–106.Google Scholar
Efromovich, S. (1999) Nonparametric Curve Estimation: Methods, Theory, and Applications. Springer.
Engle, R.F. (1982) Autoregressive conditional heteroskedasticity with estimation of U.K. inflation. Econometrica 50, 987–1008.Google Scholar
Fan, J. & I. Gijbels (1995) Data-driven bandwidth selection in local polynomial fitting: Variable bandwidth and spatial adaptation. Journal of the Royal Statistical Society, Series B 57, 371–394.Google Scholar
Fan, J., J. Jiang, C. Zhang, & Z. Zhou (2002) Time-dependent diffusion models for term structure dynamics and the stock price volatility. Statistica Sinica, forthcoming.Google Scholar
Feng, Y. (2002) An iterative plug-in algorithm for nonparametric modelling of seasonal time series. CoFE discussion paper 02/04, University of Konstanz.
Feng, Y. & S. Heiler (1998) Locally weighted autoregression. In R. Galata & H. Küchenhoff (eds.), Econometrics in Theory and Practice, Festschrift für Hans Schneeweiß, pp. 101–117. Physica-Verlag.
Gasser, T., A. Kneip, & W. Köhler (1991) A flexible and fast method for automatic smoothing. Journal of American Statistical Association 86, 643–652.Google Scholar
Härdle, W., H. Liang, & J. Gao (2000) Partially Linear Models. Springer.
Härdle, W., V. Spokoiny, & G. Teyssière (2000) Adaptive Estimation for a Time Inhomogeneous Stochastic-Volatility Model. Discussion paper SFB 373, Humboldt University.
Härdle, W., A.B. Tsybakov, & L. Yang (1998) Nonparametric vector autoregression. Journal of Statistical Planning and Inference 68, 221–245.Google Scholar
Hart, J.D. (1991) Kernel regression estimation with time series errors. Journal of the Royal Statistical Society, Series B 53, 173–188.Google Scholar
He, C. & T. Teräsvirta (1999a) Fourth moment structure of the GARCH(p,q) process. Econometric Theory 15, 824–846.Google Scholar
He, C. & T. Teräsvirta (1999b) Properties of autocorrelation function of squared observations for second-order GARCH processes under two sets of parameter constraints. Journal of Time Series Analysis 20, 23–30.Google Scholar
Ibragimov, I.A. & Yu.V. Linnik (1971) Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff.
Karanasos, M. (1999) The second moment and autocovariance function of the squared errors of the GARCH model. Journal of Econometrics 90, 63–76.Google Scholar
Lee, S.-W. & B.E. Hansen (1994) Asymptotic theory for the GARCH(1,1) quasi-maximum likelihood estimator. Econometric Theory 10, 29–52.Google Scholar
Ling, S. (1999) On probability properties of a double threshold ARMA conditional heteroskedasticity model. Journal of Applied Probability 36, 688–705.Google Scholar
Ling, S. & W.K. Li (1997) On fractional integrated autoregressive moving-average time series models with conditional heteroskedasticity. Journal of the American Statistical Association 92, 1184–1194.Google Scholar
Ling, S. & M. McAleer (2002) Necessary and sufficient moment conditions for the GARCH(r,s) and asymmetric power GARCH(r,s) models. Econometric Theory 18, 722–729.Google Scholar
Lumsdaine, R.L. (1996) Consistency and asymptotic normality of the quasi-maximum likelihood estimator in IGARCH(1,1) and GARCH(1,1) models. Econometrica 64, 575–596.Google Scholar
Mercurio, D. & V. Spokoiny (2002) Statistical Inference for Time-Inhomogeneous Volatility Models. Discussion paper SFB 373, Humboldt University.
Mikosch, T. & C. Stărică (2004) Change of structure in financial time series, long range dependence and the GARCH models. Review of Economics and Statistics, to appear.Google Scholar
Müller, H.G. (1988) Nonparametric Analysis of Longitudinal Data. Springer.
Ruppert, D., S.J. Sheather, & M.P. Wand (1995) An effective bandwidth selector for local least squares regression. Journal of the American Statistical Association 90, 1257–1270.Google Scholar
Ruppert, D. & M.P. Wand (1994) Multivariate locally weighted least squares regression. Annals of Statistics 22, 1346–1370.Google Scholar
Yao, Q. & B. Morgan (1999) Empirical transform estimation for indexed stochastic models. Journal of the Royal Statistical Society, Series B 61, 127–141.Google Scholar