Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Abbritti, Mirko
Carcel, Hector
Gil-Alana, Luis A.
and
Moreno, Antonio
2017.
Term Premium and Quantitative Easing in a Fractionally Cointegrated Yield Curve.
SSRN Electronic Journal ,
Johansen, Soren
and
Nielsen, Morten rregaard
2017.
Testing the CVAR in the Fractional CVAR Model.
SSRN Electronic Journal ,
Nielsen, Morten Ørregaard
and
Shibaev, Sergei S.
2018.
Forecasting Daily Political Opinion Polls Using the Fractionally Cointegrated Vector Auto-Regressive Model.
Journal of the Royal Statistical Society Series A: Statistics in Society,
Vol. 181,
Issue. 1,
p.
3.
DUAN, KUN
Mishra, Tapas
Parhi, Mamata
and
Wolfe, Simon
2018.
Value the 'Memory'!: Identifying Macroeconomic Variations in Housing Price Determination.
SSRN Electronic Journal,
Johansen, Søren
and
Nielsen, Morten Ørregaard
2018.
Testing the CVAR in the Fractional CVAR Model.
Journal of Time Series Analysis,
Vol. 39,
Issue. 6,
p.
836.
Chevillon, Guillaume
Hecq, Alain
and
Laurent, Sébastien
2018.
Generating univariate fractional integration within a large VAR(1).
Journal of Econometrics,
Vol. 204,
Issue. 1,
p.
54.
Johansen, Soren
and
Nielsen, Morten Orregaard
2018.
Nonstationary Cointegration in the Fractionally Cointegrated VAR Model.
SSRN Electronic Journal ,
Carlini, Federico
and
Santucci de Magistris, Paolo
2018.
Resuscitating the Co-Fractional Model of Granger (1986).
SSRN Electronic Journal,
Dolatabadi, Sepideh
Narayan, Paresh Kumar
Nielsen, Morten Ørregaard
and
Xu, Ke
2018.
Economic significance of commodity return forecasts from the fractionally cointegrated VAR model.
Journal of Futures Markets,
Vol. 38,
Issue. 2,
p.
219.
Johansen, Søren
and
Nielsen, Morten Ørregaard
2019.
Nonstationary Cointegration in the Fractionally Cointegrated VAR Model.
Journal of Time Series Analysis,
Vol. 40,
Issue. 4,
p.
519.
Yaya, OlaOluwa S.
Ogbonna, Ahamuefula E.
and
Olubusoye, Olusanya E.
2019.
How persistent and dynamic inter-dependent are pricing of Bitcoin to other cryptocurrencies before and after 2017/18 crash?.
Physica A: Statistical Mechanics and its Applications,
Vol. 531,
Issue. ,
p.
121732.
Kapetanios, George
Papailias, Fotis
and
Taylor, A. M. Robert
2019.
A Generalised Fractional Differencing Bootstrap for Long Memory Processes.
Journal of Time Series Analysis,
Vol. 40,
Issue. 4,
p.
467.
Hualde, Javier
and
Nielsen, Morten Ørregaard
2020.
TRUNCATED SUM OF SQUARES ESTIMATION OF FRACTIONAL TIME SERIES MODELS WITH DETERMINISTIC TRENDS.
Econometric Theory,
Vol. 36,
Issue. 4,
p.
751.
Moklyachuk, M. P.
and
Luz, M. M.
2020.
Minimax-robust estimation problems for sequences with periodically stationary increments observed with noise.
Bulletin of Taras Shevchenko National University of Kyiv. Series: Physics and Mathematics,
p.
68.
Robinson, Peter M.
and
Velasco, Carlos
2020.
ESTIMATION FOR DYNAMIC PANEL DATA WITH INDIVIDUAL EFFECTS.
Econometric Theory,
Vol. 36,
Issue. 2,
p.
185.
Stoupos, Nikolaos
and
Kiohos, Apostolos
2020.
Recent Advances and Applications in Alternative Investments.
p.
143.
Bravo Caro, José Manuel
Golpe, Antonio A.
Iglesias, Jesús
and
Vides, José Carlos
2020.
A new way of measuring the WTI – Brent spread. Globalization, shock persistence and common trends..
Energy Economics,
Vol. 85,
Issue. ,
p.
104546.
Hassler, Uwe
and
Hosseinkouchack, Mehdi
2020.
Estimating the mean under strong persistence.
Economics Letters,
Vol. 188,
Issue. ,
p.
108950.
Nielsen, Morten Ørregaard
and
Noël, Antoine L.
2021.
To infinity and beyond: Efficient computation of ARCH(∞) models.
Journal of Time Series Analysis,
Vol. 42,
Issue. 3,
p.
338.
Quineche, Ricardo
2021.
Consumption, Aggregate Wealth and Expected Stock Returns: An FCVAR Approach.
Journal of Time Series Econometrics,
Vol. 13,
Issue. 1,
p.
21.
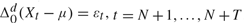 ${\rm{\Delta }}_0^d \left( {X_t - \mu } \right) = \varepsilon _t ,t = N + 1, \ldots ,N + T$, conditional on X1,..., XN. We derive an expression for the second-order bias of
${\rm{\Delta }}_0^d \left( {X_t - \mu } \right) = \varepsilon _t ,t = N + 1, \ldots ,N + T$, conditional on X1,..., XN. We derive an expression for the second-order bias of 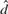 $\hat d$ as a function of the initial values, Xt, t = – N0 + 1,..., N, and we investigate the effect on the bias of setting aside the first N observations as initial values. We compare
$\hat d$ as a function of the initial values, Xt, t = – N0 + 1,..., N, and we investigate the effect on the bias of setting aside the first N observations as initial values. We compare 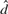 $\hat d$ with an estimator,
$\hat d$ with an estimator, 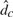 $\hat d_c $, derived similarly but by choosing μ = C. We find, both theoretically and using a data set on voting behavior, that in many cases, the estimation of the parameter μ picks up the effect of the initial values even for the choice N = 0.
$\hat d_c $, derived similarly but by choosing μ = C. We find, both theoretically and using a data set on voting behavior, that in many cases, the estimation of the parameter μ picks up the effect of the initial values even for the choice N = 0.