Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T18:13:25.332Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL BANDWIDTH SELECTION IN NONLINEAR COINTEGRATING REGRESSION

Published online by Cambridge University Press:  14 December 2020

Qiying Wang  and
Peter C. B. Phillips
Qiying Wang
Affiliation:
School of Mathematics and Statistics, University of Sydney
Peter C. B. Phillips*
Affiliation:
Yale University University of Auckland University of Southampton Singapore Management University
*
Address correspondence to Peter C. B. Phillips, Yale University, New Haven, CT, USA; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study optimal bandwidth selection in nonparametric cointegrating regression where the regressor is a stochastic trend process driven by short or long memory innovations. Unlike stationary regression, the optimal bandwidth is found to be a random sequence which depends on the sojourn time of the process. All random sequences 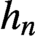$h_{n}$ that lie within a wide band of rates as the sample size 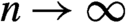$n\rightarrow \infty $ have the property that local level and local linear kernel estimates are asymptotically normal, which enables inference and conveniently corresponds to limit theory in the stationary regression case. This finding reinforces the distinctive flexibility of data-based nonparametric regression procedures for nonstationary nonparametric regression. The present results are obtained under exogenous regressor conditions, which are restrictive but which enable flexible data-based methods of practical implementation in nonparametric predictive regressions within that environment.

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 6: SPECIAL ISSUE IN HONOR OF BENEDIKT M PÖTSCHER , December 2023 , pp. 1325 - 1337
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Footnotes

The authors thank the Guest Co-Editor, Professor Ingmar Prucha, and one referee for helpful comments on the original manuscript, which have led to many improvements. Wang acknowledges research support from the Australian Research Council and Phillips acknowledges research support from the NSF under Grant No. SES 18-50860 and the Kelly Fund at the University of Auckland.

References

REFERENCES

Bandi, F.M., Corradi, V., & Wilhelm, D. (2012) Data-Driven Bandwidth Selection for Nonparametric Nonstationary Regressions. Working paper, Johns Hopkins University.CrossRefGoogle Scholar
Chan, N. & Wang, Q. (2014) Uniform convergence for non-parametric estimators with non-stationary data. Econometric Theory 30, 1110–1133.CrossRefGoogle Scholar
Chan, N. & Wang, Q. (2015) Nonlinear regression with nonstationary time series. Journal of Econometrics 185, 182–195.CrossRefGoogle Scholar
de Jong, R.M. (2004) Addendum to: Asymptotics for nonlinear transformations of integrated time series. Econometric Theory 20, 627–635.CrossRefGoogle Scholar
Duffy, J.A. (2017a) Uniformly Valid Inference in Nonparametric Predictive Regression. Working paper, University of Oxford.Google Scholar
Duffy, J.A. (2017b) Uniform convergence rates over maximal domains in structural nonparametric cointegrating regression. Econometric Theory 33, 1387–1417.CrossRefGoogle Scholar
Kasparis, I., Andreou, E., & Phillips, P.C.B. (2015) Nonparametric predictive regression. Journal of Econometrics 185, 468–494.CrossRefGoogle Scholar
Park, J.Y. & Phillips, P.C.B. (1999) Asymptotics for nonlinear transformations of integrated time series. Econometric Theory 15, 269–298.CrossRefGoogle Scholar
Park, J.Y. & Phillips, P.C.B. (2000) Nonstationary binary choice. Econometrica 68, 1249–1280.CrossRefGoogle Scholar
Park, J.Y. & Phillips, P.C.B. (2001) Nonlinear regressions with integrated time series. Econometrica 69, 117–161.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007) Limit theory for moderate deviations from a unit root. Journal of Econometrics 136, 115–130.CrossRefGoogle Scholar
Pötscher, B.M. (2004) Nonlinear functions and convergence to Brownian motion: Beyond the continuous mapping theorem. Econometric Theory 20, 1–22.CrossRefGoogle Scholar
Wang, Q. (2014) Martingale limit theorem revisited and nonlinear cointegrating regression. Econometric Theory 30, 509–535.CrossRefGoogle Scholar
Wang, Q. (2015) Limit Theorems for Nonlinear Cointegrating Regression. World Scientific.CrossRefGoogle Scholar
Wang, Q. & Phillips, P.C.B. (2009a) Asymptotic theory for local time density estimation and nonparametric cointegrating regression. Econometric Theory 25, 710–738.CrossRefGoogle Scholar
Wang, Q. & Phillips, P.C.B. (2009b) Structural nonparametric cointegrating regression. Econometrica 77, 1901–1948.Google Scholar
Wang, Q. & Phillips, P.C.B. (2011) Asymptotic theory for zero energy functionals with nonparametric regression applications. Econometric Theory 27, 235–259.CrossRefGoogle Scholar
Wang, Q. & Phillips, P.C.B. (2016) Nonparametric cointegrating regression with endogeneity and long memory. Econometric Theory 32, 359–401.CrossRefGoogle Scholar