Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-04T21:29:13.963Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ORDER OF MAGNITUDE OF SUMS OF NEGATIVE POWERS OF INTEGRATED PROCESSES

Published online by Cambridge University Press:  12 November 2012

Benedikt M. Pötscher
Benedikt M. Pötscher*
Affiliation:
University of Vienna
*
*Address correspondence to the author at Department of Statistics, University of Vienna, Universitätsstrasse 5, A-1010, Vienna, Austria; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

Upper and lower bounds on the order of magnitude of 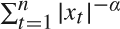$\sum\nolimits_{t = 1}^n {\lefttnq#x007C; {x_t } \righttnq#x007C;^{ - \alpha } } $, where xt is an integrated process, are obtained. Furthermore, upper bounds for the order of magnitude of the related quantity 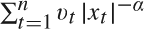$\sum\nolimits_{t = 1}^n {v_t } \lefttnq#x007C; {x_t } \righttnq#x007C;^{ - \alpha } $, where vt are random variables satisfying certain conditions, are also derived.

Type
Miscellanea
Information
Econometric Theory , Volume 29 , Issue 3 , June 2013 , pp. 642 - 658
Copyright
Copyright © Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

I thank Kalidas Jana for inquiring about the order of magnitude of some of the quantities now treated in the paper. I am indebted to Robert de Jong for comments on an early draft that have led to an improvement in Theorem 1. I am grateful to Istvan Berkes, Hannes Leeb, David Preinerstorfer, Zhan Shi, the referees, and the editor Peter Phillips for helpful comments.

References

Berkes, I. & Horvath, L. (2006) Convergence of integral functionals of stochastic processes. Econometric Theory 22, 304–322.CrossRefGoogle Scholar
Borodin, A.N. & Ibragimov, I.A. (1995) Limit theorems for functionals of random walks. Proceedings of the Steklov Institute of Mathematics 195(2).Google Scholar
Christopeit, N. (2009) Weak convergence of nonlinear transformations of integrated processes: The multivariate case. Econometric Theory 25, 1180–1207.CrossRefGoogle Scholar
Chung, K.L. (2001) A Course in Probability Theory, 3rd ed. Academic Press.Google Scholar
Chung, K.L. & Williams, R.J. (1990) Introduction to Stochastic Integration, 2nd ed. Birkhäuser.CrossRefGoogle Scholar
de Jong, R.M. (2004) Addendum to “Asymptotics for nonlinear transformations of integrated time series.” Econometric Theory 20, 627–635.CrossRefGoogle Scholar
de Jong, R.M. & Wang, C. (2005) Further results on the asymptotics for nonlinear transformations of integrated time series. Econometric Theory 21, 413–430.CrossRefGoogle Scholar
Ibragimov, R. & Phillips, P.C.B. (2008) Regression asymptotics using martingale convergence methods. Econometric Theory 24, 888–947.CrossRefGoogle Scholar
Jeganathan, P. (2004) Convergence of functionals of sums of R.V.s to local times of fractional stable motions. Annals of Probability 32, 1771–1795.CrossRefGoogle Scholar
Lai, T.L. & Wei, C.Z. (1982) Least squares estimates in stochastic regression models with applications to identification and control of dynamic systems. Annals of Statistics 10, 154–166.CrossRefGoogle Scholar
Park, J.Y. & Phillips, P.C.B. (1999) Asymptotics for nonlinear transformations of integrated time series. Econometric Theory 15, 269–298.CrossRefGoogle Scholar
Pötscher, B.M. (2004) Nonlinear functionals and convergence to Brownian motion: Beyond the continuous mapping theorem. Econometric Theory 20, 1–22.CrossRefGoogle Scholar