Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T17:54:40.247Z Has data issue: false hasContentIssue false
  • English
  • Français

NONPARAMETRIC ESTIMATION OF HOMOGENEOUS FUNCTIONS

Published online by Cambridge University Press:  06 June 2003

Gautam Tripathi  and
Woocheol Kim
Gautam Tripathi
Affiliation:
University of Wisconsin-Madison
Woocheol Kim
Affiliation:
Humboldt-Universität zu Berlin
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the regression 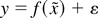, where 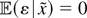and the exact functional form of f is unknown, although we do know that f is homogeneous of known degree r. Using a local linear approach, we examine two ways of nonparametrically estimating f: (i) a “direct” approach and (ii) a “projection based” approach. We show that depending upon the nature of the conditional variance 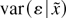, one approach may be asymptotically better than the other. Results of a small simulation experiment are presented to support our findings.We thank Don Andrews and an anonymous referee for comments that greatly improved this paper. The first author thanks Professor Wolfgang Härdle for hospitality at the Institute of Statistics and Econometrics, Humboldt University, Berlin, where part of this research was carried out. Financial support to the first author from Sonderforschungsbereich 373 (“Quantifikation und Simulation Ökonomischer Prozesse”) and the NSF via grants SES-0111917 and SES-0214081 is also gratefully acknowledged.

Type
Research Article
Information
Econometric Theory , Volume 19 , Issue 4 , August 2003 , pp. 640 - 663
Copyright
© 2003 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arrow, K., H. Chenery, B. Minhas, & R. Solow (1961) Capital-labor substitution and economic efficiency. Review of Economics and Statistics 43, 225–250.Google Scholar
Bierens, H.J. (1985) Kernel estimators of regression functions. In W.A. Barnett, J. Powell, & G. Tauchen (eds.), Nonparametric and Semiparametric Methods in Econometrics and Statistics: Proceedings of the Fifth International Symposium in Economic Theory and Econometrics, pp. 99–144. Cambridge, UK: Cambridge University Press.
Fan, J. (1992) Design adaptive nonparametric regression. Journal of the American Statistical Association 87, 998–1004.Google Scholar
Gallant, A.R. (1981) On the bias in flexible functional forms and an essentially unbiased form: The Fourier flexible form. Journal of Econometrics 15, 211–246.Google Scholar
Gozalo, P. & O. Linton (2000) Local nonlinear least squares: Using parametric information in nonparametric regression. Journal of Econometrics 99, 63–106.Google Scholar
Härdle, W. (1989) Applied Nonparametric Regression. New York: Cambridge University Press.
Härdle, W. & O. Linton (1994) Applied nonparametric methods. In R. Engle & D. McFadden (eds.), Handbook of Econometrics, vol. IV, pp. 2295–2339. Amsterdam: Elsevier Science B.V.
Härdle, W. & E. Mammen (1993) Comparing nonparametric versus parametric regression fits. Annals of Statistics 21, 1926–1947.Google Scholar
Hengartner, N.W. & O.B. Linton (1996) Nonparametric regression estimation at design poles and zeros. Canadian Journal of Statistics 24, 583–591.Google Scholar
Hildreth, C. (1954) Point estimates of ordinates of concave functions. Journal of the American Statistical Association 49, 598–619.Google Scholar
Jones, M. (1993) Do not weight for heteroscedasticity in nonparametric regression. Australian Journal of Statistics 35, 89–92.Google Scholar
Matzkin, R. (1994) Restrictions of economic theory in nonparametric methods. In R. Engle & D. McFadden (eds.), Handbook of Econometrics, vol. IV, pp. 2524–2558. Elsevier Science B.V.
McFadden, D.L. (1984) Econometric analysis of qualitative response models. In Z. Griliches & M. Intriligator (eds.), Handbook of Econometrics, vol. II, pp. 1396–1457. Amsterdam: Elsevier Science B.V.
Pagan, A. & A. Ullah (1999) Nonparametric Econometrics. New York: Cambridge University Press.
Petrongolo, B. & C.A. Pissarides (2001) Looking into the black box: A survey of the matching function. Journal of Economic Literature 39, 390–431.Google Scholar
Ruppert, D. & M. Wand (1994) Multivariate locally weighted least squares regression. Annals of Statistics 22, 1346–1370.Google Scholar
Ruud, P.A. (1997) Restricted least squares subject to monotonicity and concavity constraints. In D.M. Kreps & K.F. Wallis (eds.), Advances in Economics and Econometrics: Theory and Applications, Proceedings of the Seventh World Congress, vol. 3, pp. 166–187. Cambridge, UK: Cambridge University Press.
Ryu, H.K. (1993) Maximum entropy estimation of density and regression functions. Journal of Econometrics 56, 397–440.Google Scholar
Schuster, E.F. (1972) Joint asymptotic distribution of the estimated regression function at a finite number of distinct points. Annals of Mathematical Statistics 43, 84–88.Google Scholar
Tripathi, G. (2000) Local semiparametric efficiency bounds under shape restrictions. Econometric Theory 16, 729–739.Google Scholar
Yatchew, A. (1988) Some tests of nonparametric regression models. In W. Barnett, E. Berndt, & H. White (eds.), Dynamic Econometric Modelling: Proceedings of the Third International Symposium in Economic Theory and Econometrics, pp. 121–135. Cambridge, UK: Cambridge University Press.
Yatchew, A. (1998) Nonparametric regression techniques in economics. Journal of Economic Literature 36, 669–721.Google Scholar
Yatchew, A. & L. Bos (1997) Nonparametric least squares regression and testing in economic models. Journal of Quantitative Economics 13, 81–31.Google Scholar