Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-09T09:20:08.354Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL ASYMPTOTIC NORMALITY OF GENERAL CONDITIONALLY HETEROSKEDASTIC AND SCORE-DRIVEN TIME-SERIES MODELS

Published online by Cambridge University Press:  21 March 2022

Christian Francq Open the ORCID record for Christian Francq [Opens in a new window]  and
Jean-Michel Zakoian Open the ORCID record for Jean-Michel Zakoian [Opens in a new window]
Christian Francq
Affiliation:
ENSAE-CREST, University of Lille
Jean-Michel Zakoian*
Affiliation:
ENSAE-CREST, University of Lille
*
Address correspondence to Jean-Michel Zakoïan, CREST, 5 Avenue Henri Le Chatelier, 91120 Palaiseau, France; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper establishes the local asymptotic normality property for general conditionally heteroskedastic time series models of multiplicative form, 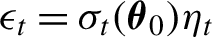$\epsilon _t=\sigma _t(\boldsymbol {\theta }_0)\eta _t$, where the volatility 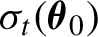$\sigma _t(\boldsymbol {\theta }_0)$ is a parametric function of 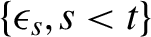$\{\epsilon _{s}, s< t\}$, and 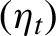$(\eta _t)$ is a sequence of i.i.d. random variables with common density 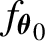$f_{\boldsymbol {\theta }_0}$. In contrast with earlier results, the finite dimensional parameter 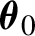$\boldsymbol {\theta }_0$ enters in both the volatility and the density specifications. To deal with nondifferentiable functions, we introduce a conditional notion of the familiar quadratic mean differentiability condition which takes into account parameter variation in both the volatility and the errors density. Our results are illustrated on two particular models: the APARCH with asymmetric Student-t distribution, and the Beta-t-GARCH model, and are extended to handle a conditional mean.

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 5 , October 2023 , pp. 1067 - 1092
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

The authors are grateful to two anonymous referees, the Co-editor, and the Editor for insightful comments, suggestions, and useful criticisms. The authors are grateful to the Agence Nationale de la Recherche (ANR), which supported this work via the Project MLforRisk (ANR-21-CE26-0007) and to the Labex ECODEC.

References

REFERENCES

Berkes, I., Horváth, L., & Kokoszka, P.S. (2003) GARCH processes: structure and estimation. Bernoulli 9, 201–227.10.3150/bj/1068128975CrossRefGoogle Scholar
Billingsley, P. (1961) The Lindeberg-Levy theorem for martingales. Proceedings of the American Mathematical Society 12, 788–792.Google Scholar
Billingsley, P. (1999) Convergence of Probability Measures , 2nd ed. John Wiley.10.1002/9780470316962CrossRefGoogle Scholar
Blasques, F., Koopman, S.J., & Lucas, A. (2014) Maximum Likelihood Estimation for Score-Driven Models. TI 2014-029/III Tinbergen Institute Discussion Paper.Google Scholar
Creal, D., Koopman, S.J., & Lucas, A. (2008) A General Framework for Observation Driven Time-Varying Parameter Models. TI 08-108/4 Tinbergen Institute Discussion paper.CrossRefGoogle Scholar
Creal, D., Koopman, S.J., & Lucas, A. (2013) Generalized autoregressive score models with applications. Journal of Applied Econometrics 28, 777–795.10.1002/jae.1279CrossRefGoogle Scholar
Drost, F.C. & Klaassen, C.A.J. (1997) Efficient estimation in semiparametric GARCH models. Journal of Econometrics 81, 193–221.10.1016/S0304-4076(97)00042-0CrossRefGoogle Scholar
Drost, F.C., Klaassen, C.A.J., & Werker, B.J.M. (1997) Adaptive estimation in time-series models. Annals of Statistics 25, 786–817.CrossRefGoogle Scholar
Francq, C. & Zakoïan, J.M. (2004) Maximum likelihood estimation of pure GARCH and ARMA-GARCH processes. Bernoulli 10, 605–637.CrossRefGoogle Scholar
Garel, B. and Hallin, M. (1995) Local asymptotic normality of multivariate ARMA processes with a linear trend. Annals of the Institute of Statistical Mathematics 47, 551–579.CrossRefGoogle Scholar
Hallin, M., Taniguchi, M., Serroukh, A., & Choy, K. (1999) Local asymptotic normality for regression models with long-memory disturbance. Annals of Statistics 27, 2054–2080.Google Scholar
Hamadeh, T. & Zakoïan, J.M. (2011) Asymptotic properties of LS and QML estimators for a class of nonlinear GARCH Processes. Journal of Statistical Planning and Inference 141, 488–507.10.1016/j.jspi.2010.06.026CrossRefGoogle Scholar
Harvey, A. (2013) Dynamic Models for Volatility and Heavy Tails . Cambridge University Press.CrossRefGoogle Scholar
Harvey, A.C. & Chakravarty, T. (2008) Beta-t-(E)GARCH. University of Cambridge, Faculty of Economics. Working paper CWPE 08340.Google Scholar
Jeganathan, P. (1995) Some aspects of asymptotic theory with applications to time series models. Econometric Theory 11, 818–887.10.1017/S0266466600009907CrossRefGoogle Scholar
Koul, H.L. & Schick, A. (1996) Adaptive estimation in a random coefficient autoregressive model. Annals of Statistics 24, 1025–1052.CrossRefGoogle Scholar
Kreiss, J.P. (1987) On adaptive estimation in stationary ARMA processes. Annals of Statistics 15, 112–133.CrossRefGoogle Scholar
Lee, S. & Taniguchi, M. (2005) Asymptotic theory for ARCH-SM models: LAN and residual empirical processes. Statistica Sinica 15, 215–234.Google Scholar
Lehmann, E.L. & Romano, J.P. (2006) Testing Statistical Hypotheses , 3rd ed. Springer-Verlag.Google Scholar
Liese, F. & Miescke, K.J. (2008) Statistical Decision Theory . Springer.Google Scholar
Lind, B. & Roussas, G. (1972) A remark on quadratic mean differentiability. Annals of Mathematical Statistics 43, 1030–1034.10.1214/aoms/1177692570CrossRefGoogle Scholar
Ling, S. & McAleer, M. (2003) On adaptative estimation in nonstationary ARMA models with GARCH errors. Annals of Statistics 31, 642–674.CrossRefGoogle Scholar
Linton, O. (1993) Adaptive estimation in ARCH models. Econometric Theory 9, 539–569.CrossRefGoogle Scholar
Robinson, P.M. & Zaffaroni, P. (2006) Pseudo-maximum likelihood estimation of ARCH(1) models. Annals of Statistic 34, 1049–1074.Google Scholar
Royer, J. (2022) Conditional Asymmetry in Power ARCH( $\infty$ ) Models. Journal of Econometrics, in press, https://doi.org/10.1016/j.jeconom.2021.10.013.CrossRefGoogle Scholar
Straumann, D. & Mikosch, T. (2006) Quasi-maximum-likelihood estimation in conditionally heteroscedastic time series: a stochastic recurrence equations approach. Annals of Statistics 34, 2449–2495.CrossRefGoogle Scholar
Swensen, A.R. (1985) The asymptotic distribution of the likelihood ratio for autoregressive time series with a regression trend. Journal of Multivariate Analysis 16, 54–70.CrossRefGoogle Scholar
van der Vaart, A.W. (1998) Asymptotic Statistics . Cambridge University Press.CrossRefGoogle Scholar
Zhu, D. & Galbraith, J.W. (2010) A generalized asymmetric Student- $t$ distribution with application to financial econometrics. Journal of Econometrics 157, 297–305.10.1016/j.jeconom.2010.01.013CrossRefGoogle Scholar