Published online by Cambridge University Press: 05 December 2016
We study the properties of the integrated score estimator (ISE), which is the Laplace version of Manski’s maximum score estimator (MMSE). The ISE belongs to a class of estimators whose basic asymptotic properties were studied in Jun, Pinkse, and Wan (2015, Journal of Econometrics 187(1), 201–216). Here, we establish that the MMSE, or more precisely 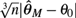 $$\root 3 \of n |\hat \theta _M - \theta _0 |$$, (locally first order) stochastically dominates the ISE under the conditions necessary for the MMSE to attain its
$$\root 3 \of n |\hat \theta _M - \theta _0 |$$, (locally first order) stochastically dominates the ISE under the conditions necessary for the MMSE to attain its 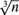 $\root 3 \of n $ convergence rate and that the ISE has the same convergence rate as Horowitz’s smoothed maximum score estimator (SMSE) under somewhat weaker conditions. An implication of the stochastic dominance result is that the confidence intervals of the MMSE are for any given coverage rate wider than those of the ISE, provided that the input parameter αn is not chosen too large. Further, we introduce an inference procedure that is not only rate adaptive as established in Jun et al. (2015), but also uniform in the choice of αn. We propose three different first order bias elimination procedures and we discuss the choice of input parameters. We develop a computational algorithm for the ISE based on the Gibbs sampler and we examine implementational issues in detail. We argue in favor of normalizing the norm of the parameter vector as opposed to fixing one of the coefficients. Finally, we evaluate the computational efficiency of the ISE and the performance of the ISE and the proposed inference procedure in an extensive Monte Carlo study.
$\root 3 \of n $ convergence rate and that the ISE has the same convergence rate as Horowitz’s smoothed maximum score estimator (SMSE) under somewhat weaker conditions. An implication of the stochastic dominance result is that the confidence intervals of the MMSE are for any given coverage rate wider than those of the ISE, provided that the input parameter αn is not chosen too large. Further, we introduce an inference procedure that is not only rate adaptive as established in Jun et al. (2015), but also uniform in the choice of αn. We propose three different first order bias elimination procedures and we discuss the choice of input parameters. We develop a computational algorithm for the ISE based on the Gibbs sampler and we examine implementational issues in detail. We argue in favor of normalizing the norm of the parameter vector as opposed to fixing one of the coefficients. Finally, we evaluate the computational efficiency of the ISE and the performance of the ISE and the proposed inference procedure in an extensive Monte Carlo study.
This paper is based on research supported by NSF grant SES–0922127. We thank the Human Capital Foundation (www.hcfoundation.ru), especially Andrey P. Vavilov, for their support of CAPCP (http://capcp.psu.edu) at the Pennsylvania State University. We thank Don Andrews, Miguel Delgado, Jeremy Fox, Bo Honoré, Joel Horowitz, Roger Koenker, Arthur Lewbel, Runze Li, Oliver Linton, Peter Robinson, Neil Wallace, Haiqing Xu, Vicky Zinde–Walsh, six anonymous referees, and numerous departmental seminar and conference participants for helpful suggestions.