Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T18:47:20.904Z Has data issue: false hasContentIssue false
  • English
  • Français

HOW LARGE IS THE JUMP DISCONTINUITY IN THE DIFFUSION COEFFICIENT OF A TIME-HOMOGENEOUS DIFFUSION?

Published online by Cambridge University Press:  03 June 2022

Christian Y. Robert
Christian Y. Robert*
Affiliation:
ENSAE and Université de Lyon
*
Address correspondence to Christian Y. Robert, Institut de Science Financière et d’Assurances, Université de Lyon, Université Lyon 1, 50 Avenue Tony Garnier, F-69007 Lyon, France; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider high-frequency observations from a one-dimensional time-homogeneous diffusion process Y. We assume that the diffusion coefficient 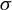$\sigma $ is continuously differentiable in y, but with a jump discontinuity at some level y, say 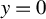$y=0$. We first study sign-constrained kernel estimators of functions of the left and right limits of 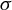$\sigma $ at 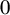$0$. These functions intricately depend on both limits. We propose a method to extricate these functions by searching for bandwidths where the kernel estimators are stable by iteration. We finally provide an estimator of the discontinuity jump size. We prove its convergence in probability and discuss its rate of convergence. A Monte Carlo study shows the finite sample properties of this estimator.

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 4 , August 2023 , pp. 848 - 880
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

The author acknowledges a considerable debt of gratitude to the Co-Editor (Professor Viktor Todorov) and to two reviewers for very fruitful comments and remarks that led to a great improvement of the first version of the paper. The author also thanks the Editor (Professor Peter C.B. Phillips) for all his help in finalizing the manuscript.

References

REFERENCES

Ait-Sahalia, Y. & Jacod, J. (2014) High-Frequency Financial Econometrics . Princeton University Press.Google Scholar
Applebaum, D. (2009) Lévy Processes and Stochastic Calculus . Cambridge University Press.CrossRefGoogle Scholar
Appuhamillage, T., Bokil, V., Thomann, E., Waymire, E., & Wood, B. (2011a) Occupation and local times for skew Brownian motion with applications to dispersion across an interface. The Annals of Applied Probability 21, 183–214.Google Scholar
Appuhamillage, T., Bokil, V., Thomann, E., Waymire, E., & Wood, B. (2011b) Corrections: Occupation and local times for skew Brownian motion with applications to dispersion across an interface. The Annals of Applied Probability 21, 2050–2051.Google Scholar
Bandi, F.M. & Nguyen, T.H. (2003) On the functional estimation of jump–diffusion models. Journal of Econometrics 116, 293–328.CrossRefGoogle Scholar
Bandi, F.M. & Phillips, P.C.B. (2003) Fully nonparametric estimation of scalar diffusion models. Econometrica 71, 241–283.CrossRefGoogle Scholar
Bibinger, M. & Winkelmann, L. (2018) Common price and volatility jumps in noisy high-frequency data. Electronic Journal of Statistics 12, 2018–2073.CrossRefGoogle Scholar
Cantrell, R. & Cosner, C. (1999) Diffusion models for population dynamics incorporating individual behavior at boundaries: Applications to refuge design. Theoretical Population Biology 55, 189–207.CrossRefGoogle ScholarPubMed
Decamps, M., Goovaerts, M., & Schoutens, W. (2006) Self exciting threshold interest rates models. International Journal of Theoretical and Applied Finance 09, 1093–1122.CrossRefGoogle Scholar
Florens-Zmirou, D. (1993) On estimating the diffusion coefficient from discrete observations. Journal of Applied Probability 30, 790–804.CrossRefGoogle Scholar
Gairat, A. & Shcherbakov, V. (2016) Density of skew Brownian motion and its functionals with application in finance. Mathematical Finance 27, 1069–1088.CrossRefGoogle Scholar
Jacod, J. (1998) Rates of convergence to the local time of a diffusion. Annales de l’Institut Henri Poincare (B) Probability and Statistics 34, 505–544.CrossRefGoogle Scholar
Jacod, J. & Todorov, V. (2010) Do price and volatility jump together? The Annals of Applied Probability 20, 1425–1469.CrossRefGoogle Scholar
Jiang, G.J. & Knight, J.L. (1997) A nonparametric approach to the estimation of diffusion processes, with an application to a short-term interest rate model. Econometric Theory 13, 615–645.CrossRefGoogle Scholar
Johannes, M. (2004) The statistical and economic role of jumps in continuous-time interest rate models. The Journal of Finance 59, 227–260.CrossRefGoogle Scholar
Karatzas, I. & Shreve, S.E. (2000) Brownian Motion and Stochastic Calculus , 2nd Edition. Springer.Google Scholar
Keilson, J. & Wellner, J.A. (1978) Oscillating Brownian motion. Journal of Applied Probability 15, 300–310.CrossRefGoogle Scholar
LaBolle, E.M., Quastel, J., Fogg, G.E., & Gravner, J. (2000) Diffusion processes in composite porous media and their numerical integration by random walks: Generalized stochastic differential equations with discontinuous coefficients. Water Resources Research 36, 651–662.CrossRefGoogle Scholar
LeGall, J.F. (1984) One dimensional stochastic differential equations involving the local times of the unknown process. In Truman, A. & Williams, D. (eds.) Stochastic Analysis and Applications , Lecture Notes in Mathematics, pp. 51–82. Springer.CrossRefGoogle Scholar
Lejay, A. (2006) On the constructions of the skew Brownian motion. Probability Surveys 3, 413–466.CrossRefGoogle Scholar
Lejay, A., Mordecki, E., & Torres, S. (2013) Is a Brownian motion skew? Scandinavian Journal of Statistics 41, 346–364.CrossRefGoogle Scholar
Lejay, A., Mordecki, E., & Torres, S. (2019) Two consistent estimators for the skew Brownian motion. ESAIM: Probability and Statistics 23, 567–583.CrossRefGoogle Scholar
Lejay, A. & Pigato, P. (2018) Statistical estimation of the oscillating Brownian motion. Bernoulli 24, 3568–3602.CrossRefGoogle Scholar
Li, J., Todorov, V., & Tauchen, G. (2017) Jump regressions. Econometrica 85, 173–195.CrossRefGoogle Scholar
Mancini, C. & Renò, R. (2011) Threshold estimation of Markov models with jumps and interest rate modeling. Journal of Econometrics 160, 77–92.CrossRefGoogle Scholar
Mazzonetto, S. (2021) Rates of convergence to the local time of oscillating and skew Brownian motions. Preprint, arXiv:1912.04858.Google Scholar
Nakao, S. (1972) On the pathwise uniqueness of solutions of one-dimensional stochastic differential equations. Osaka Journal of Mathematics 9, 513–518.Google Scholar
Pigato, P. (2019) Extreme at-the-money skew in a local volatility model. Finance and Stochastics 23, 827–859.CrossRefGoogle Scholar
Protter, P. (2005) Stochastic Integration and Differential Equation , 2nd Edition. Springer.CrossRefGoogle Scholar
Renò, R. (2008) Nonparametric estimation of the diffusion coefficient of stochastic volatility models. Econometric Theory 24, 1174–1206.CrossRefGoogle Scholar
Renyi, A. (1963) On stable sequences of events. Sankhya: The Indian Journal of Statistics, Series A (1961–2002) 25, 293–302.Google Scholar
Rossello, D. (2012) Arbitrage in skew Brownian motion models. Insurance: Mathematics and Economics 50, 50–56.Google Scholar
Stanton, R. (1997) A nonparametric model of term structure dynamics and the market price of interest rate risk. The Journal of Finance 52, 1973–2002.CrossRefGoogle Scholar
Todorov, V. & Tauchen, G. (2011) Volatility jumps. Journal of Business & Economic Statistics 29, 356–371.CrossRefGoogle Scholar
Walsh, J.B. (1978) A diffusion with a discontinuous local time. In Temps locaux , Société mathématique de France, vol. 52–53. Astérisque.Google Scholar
Supplementary material: PDF

Robert supplementary material

Robert supplementary material
Download Robert supplementary material(PDF)
PDF 341.4 KB