Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T05:58:27.102Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATION OF UNIT ROOT SPATIAL DYNAMIC PANEL DATA MODELS

Published online by Cambridge University Press:  17 February 2010

Jihai Yu  and
Lung-fei Lee
Jihai Yu
Affiliation:
University of Kentucky
Lung-fei Lee*
Affiliation:
Ohio State University
*
*Address correspondence to Lung-fei Lee, Department of Economics, Ohio State University, Columbus, OH 43210, USA; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

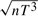This paper examines the asymptotics of the QMLE for unit root dynamic panel data models with spatial effect and fixed effects. We consider a unit root dynamic panel data model with spatially correlated disturbances and a unit root spatial dynamic panel data model. For both models the estimate of the dynamic coefficient is consistent and the estimates of other parameters are 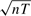consistent, and all of them are asymptotically normal. For the latter model the sum of the contemporaneous spatial effect and dynamic spatial effect converges at 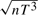rate. We also propose a bias-correction procedure so that the asymptotic biases of those estimates are eliminated as long as n/T3 → 0.

Type
ARTICLES
Information
Econometric Theory , Volume 26 , Issue 5 , October 2010 , pp. 1332 - 1362
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, T.W. & Hsiao, C. (1982) Formulation and estimation of dynamic models using panel data. Journal of Econometrics 18, 47–82.CrossRefGoogle Scholar
Baltagi, B.H., Song, S.H., Jung, B.C., & Koh, W. (2007) Testing for serial correlation, spatial autocorrelation and random effects using panel data. Journal of Econometrics 140, 5–51.Google Scholar
Baltagi, B.H., Song, S.H., & Koh, W. (2003) Testing panel data regression models with spatial error correlation. Journal of Econometrics 117, 123–150.CrossRefGoogle Scholar
Choi, I. (2006) Nonstationary panels. In Mills, T.C. & Patterson, K. (eds.), Palgrave Handbook of Econometrics, vol. 1, Ch. 13, Econometric Theory, pp. 511–539. Palgrave Macmillan.Google Scholar
Hahn, J. & Kuersteiner, G. (2002) Asymptotically unbiased inference for a dynamic panel model with fixed effects when both n and T are large. Econometrica 70, 1639–1657.CrossRefGoogle Scholar
Kao, C. & Chiang, M.H. (2000) On the estimation and inference of a cointegrated regression in panel data. In Baltagi, B.H. (ed.), Advances in Econometrics 15, pp. 179–222. JAI.Google Scholar
Kapoor, M., Kelejian, H.H., & Prucha, I.R. (2007) Panel data models with spatially correlated error components. Journal of Econometrics 140, 97–130.CrossRefGoogle Scholar
Kelejian, H.H. & Prucha, I.R. (1998) A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbance. Journal of Real Estate Finance and Economics 17:1, 99–121.CrossRefGoogle Scholar
Kelejian, H.H. & Prucha, I.R. (2001) On the asymptotic distribution of the Moran I test statistic with applications. Journal of Econometrics 104, 219–257.CrossRefGoogle Scholar
Keller, W. & Shiue, C.H. (2007) The origin of spatial interaction. Journal of Econometrics 140, 304–332Google Scholar
Korniotis, G.M. (2005) A Dynamic Panel Estimator with Both Fixed and Spatial Effects. Working paper, University of Notre Dame.Google Scholar
Lee, L.F. (2004) Asymptotic distributions of quasi-maximum likelihood estimators for spatial econometric models. Econometrica 72, 1899–1925.Google Scholar
Lee, L.F. (2007) GMM and 2SLS estimation of mixed regressive, spatial autoregressive models. Journal of Econometrics 137, 489–514.Google Scholar
Moon, H.R. & Perron, B. (2004) Testing for a unit root in panels with dynamic factors. Journal of Econometrics 122, 81–126.CrossRefGoogle Scholar
Pedroni, P. (2000) Fully modified OLS for heterogeneous cointegrated panels and the case of purchasing power parity. In Baltagi, B.H. (ed.), Advances in Econometrics 15, pp. 93–130. JAI.Google Scholar
Phillips, P.C.B. & Moon, H. (1999) Linear regression limit theory for nonstationary panel data. Econometrica 67, 1057–1112.CrossRefGoogle Scholar
Yu, J., de Jong, R., & Lee, L.F. (2007) Quasi-Maximum Likelihood Estimators for Spatial Dynamic Panel Data with Fixed Effects when Both n and T Are Large: A Nonstationary Case. Working paper, Ohio State University.Google Scholar
Yu, J., de Jong, R., & Lee, L.F. (2008) Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large. Journal of Econometrics 146, 118–134.Google Scholar
Yu, J. & Lee, L.F. (2009) Convergence: A Spatial Dynamic Panel Data Approach. Working paper, Ohio State University.Google Scholar