Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T18:25:01.605Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATION OF THE LONG-RUN AVERAGE RELATIONSHIP IN NONSTATIONARY PANEL TIME SERIES

Published online by Cambridge University Press:  01 December 2004

Yixiao Sun
Yixiao Sun
Affiliation:
University of California, San Diego
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes a new class of estimators of the long-run average relationship in nonstationary panel time series. The estimators are based on the long-run average variance estimate using bandwidth equal to T. The new estimators include the pooled least squares estimator and the fixed effects estimator as special cases. It is shown that the new estimators are consistent and asymptotically normal under both the sequential limit, wherein T → ∞ followed by n → ∞, and the joint limit where T,n → ∞ simultaneously. The rate condition for the joint limit to hold is relaxed to 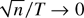, which is less restrictive than the rate condition n/T → 0, as imposed by Phillips and Moon (1999, Econometrica 67, 1057–1111). By exponentiating existing kernels, this paper introduces a new approach to generating kernels and shows that these exponentiated kernels can deliver more efficient estimates of the long-run average coefficient.I am grateful to Bruce Hansen, Peter Phillips, Zhijie Xiao, and three anonymous referees for constructive comments and suggestions. All errors are mine alone.

Type
Research Article
Information
Econometric Theory , Volume 20 , Issue 6 , December 2004 , pp. 1227 - 1260
Copyright
© 2004 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, D.W.K. (1991) Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59, 817–854.Google Scholar
Andrews, D.W.K. (2003) Cross-Section Regression with Common Shocks. Cowles Foundation Discussion paper 1428, Yale University.
Baltagi, B.H. & C. Kao (2000) Nonstationary panels, panel cointegration, and dynamic panels: A survey. Advances in Econometrics 15, 7–51.Google Scholar
Billingsley, P. (1999) Convergence of Probability Measures. Wiley.
Conley, T.G. (1999) GMM estimation with cross sectional dependence. Journal of Econometrics 92, 1–45.Google Scholar
de Jong, R.M. & J. Davidson (2000) Consistency of kernel estimators of heteroskedastic and autocorrelated covariance matrices. Econometrica 68, 407–424.Google Scholar
Engle, R.F. & C.W.J. Granger (1987) Cointegration and error correction: Representation, estimation and testing. Econometrica 55, 251–276.Google Scholar
Hannan, E.J. (1970) Multiple Time Series. Wiley.
Hansen, B.E. (1992) Consistent covariance matrix estimation for dependent heterogenous processes. Econometrica 60, 967–972.Google Scholar
Jansson, M. (2004) The error of rejection probability in simple autocorrelation robust tests. Econometrica 72, 937–946.Google Scholar
Kao, C. (1999) Spurious regression and residual-based tests for cointegration in panel data. Journal of Econometrics 90, 1–44.Google Scholar
Kiefer, N.M. & T.J. Vogelsang (2002a) Heteroskedasticity-autocorrelation robust testing using bandwidth equal to sample size. Econometric Theory 18, 1350–1366.Google Scholar
Kiefer, N.M. & T.J. Vogelsang (2002b) Heteroskedasticity-autocorrelation robust standard errors using the Bartlett kernel without truncation. Econometrica 70, 2093–2095.Google Scholar
Kiefer, N.M. & T.J. Vogelsang (2003) A New Asymptotic Theory for Heteroskedasticity-Autocorrelation Robust Tests. Working paper, Department of Economics, Cornell University.
Magnus, J.R. & H. Neudecker (1979) The commutation matrix: Some properties and applications. Annals of Statistics 7, 381–394.Google Scholar
Makela, T. (2002) Long Run Covariance Based Inference in Nonstationary Panels with Large Cross Section. Working paper, Department of Economics, Yale University.
Nabeya, S. & K. Tanaka (1988) Asymptotic theory of a test for the consistency of regression coefficients against the random walk alternative. Annals of Statistics 16, 218–235.Google Scholar
Newey, W.K. & K.D. West (1987) A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55, 703–708.Google Scholar
Parzen, E. (1957) On the consistent estimates of the spectrum of a stationary time series. Annals of Mathematical Statistics 28, 329–348.Google Scholar
Pedroni, P. (1995) Panel Cointegration: Asymptotic and Finite Sample Properties of Pooled Time Series Tests, with an Application to the PPP Hypothesis. Indiana University Working Papers in Economics 95–013.
Phillips, P.C.B. & H.R. Moon (1999) Linear regression limit theory for nonstationary panel data. Econometrica 67, 1057–1111.Google Scholar
Phillips, P.C.B. & H.R. Moon (2000) Nonstationary panel data analysis: An overview of some recent developments. Econometric Reviews 19(3), 263–286.Google Scholar
Phillips, P.C.B. & V. Solo (1992) Asymptotics for linear processes. Annals of Statistics 20, 971–1001.Google Scholar
Phillips, P.C.B. & D. Sul (2003) Dynamic panel estimation and homogeneity testing under cross sectional dependence. Econometrics Journal 6, 217–259.Google Scholar
Phillips, P.C.B., Y. Sun, & S. Jin (2003a) Consistent HAC Estimation and Robust Regression Testing Using Sharp Origin Kernels with No Truncation. Cowles Foundation Discussion paper 1407; available at http://cowles.econ.yale.edu/P/cd/d14a/d1407.pdf.
Phillips, P.C.B., Y. Sun, & S. Jin (2003b) Long Run Variance Estimation Using Steep Origin Kernels without Truncation. Cowles Foundation Discussion paper 1437; available at http://cowles.econ.yale.edu/P/cd/d14a/d1437.pdf.
Shorack, G.R. & J.A. Weller (1986) Empirical Processes with Applications to Statistics. Wiley.
Sun, Y. (2004) A convergent t-statistic in spurious regressions. Econometric Theory 20, 943–962.Google Scholar
Sun, Y. (2003) Estimation of the Long-Run Average Relationship in Nonstationary Panel Time Series. Department of Economics Working paper 2003-06, University of California, San Diego.
White, H. (1980) A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48, 817–838.Google Scholar