Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T18:26:39.175Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATION AND INFERENCE FOR MOMENTS OF RATIOS WITH ROBUSTNESS AGAINST LARGE TRIMMING BIAS

Published online by Cambridge University Press:  23 February 2021

Yuya Sasaki  and
Takuya Ura
Yuya Sasaki
Affiliation:
Vanderbilt University
Takuya Ura*
Affiliation:
University of California, Davis
*
Address correspondence to Takuya Ura, Department of Economics, University of California Davis, Davis, California, USA; email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Researchers often trim observations with small values of the denominator A when they estimate moments of the form 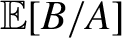$\mathbb {E}[B/A]$ . Large trimming is common in practice to reduce variance, but it incurs a large bias. This paper provides a novel method of correcting the large trimming bias. If a researcher is willing to assume that the joint distribution between A and B is smooth, then the trimming bias may be estimated well. Along with the proposed bias correction method, we also develop an inference method. Practical advantages of the proposed method are demonstrated through simulation studies, where the data generating process entails a heavy-tailed distribution of 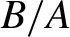$B/A$ . Applying the proposed method to the Compustat database, we analyze the history of external financial dependence of U.S. manufacturing firms for years 2000–2010.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 1 , February 2022 , pp. 66 - 112
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

First arXiv date: 4 September 2017 (arXiv:1709.00981). We benefited from useful comments by Peter C. B. Phillips (editor), Arthur Lewbel (co-editor), anonymous referees, numerous researchers, seminar participants at Australian National University, University of Bristol, University of British Columbia, Chinese University of Hong Kong, Duke University, Emory University, Fudan University, Hong Kong University of Science and Technology, University of Melbourne, Monash University, Northwestern University, University of Sydney, University of California Davis, University of California San Diego, University of New South Wales, and University of Technology Sydney, and conference participants at 2018 Asian Meeting of the Econometric Society, 2018 Cemmap Advances in Econometrics, 2018 China Meeting of the Econometric Society, 2019 Asian Meeting of the Econometric Society, 2018 International Association for Applied Econometrics Annual Conference, and New York Camp Econometrics XIII. All remaining errors are ours.

References

REFERENCES

Andrews, D.W. (1991) Asymptotic normality of series estimators for nonparametric and semiparametric regression models. Econometrica 59, 307–345.CrossRefGoogle Scholar
Andrews, D.W. & Schafgans, M.M.A. (1998) Semiparametric estimation of the intercept of a sample selection model. Review of Economic Studies 65, 497–517.CrossRefGoogle Scholar
Antoine, B. & Renault, E. (2009) Efficient GMM with nearly-weak instruments. Econometrics Journal, 12, S135–S171.CrossRefGoogle Scholar
Antoine, B. & Renault, E. (2012) Efficient minimum distance estimation with multiple rates of convergence. Journal of Econometrics 170, 350–367.CrossRefGoogle Scholar
Belloni, A., Chernozhukov, V., Chetverikov, D., & Kato, K. (2015) Some new asymptotic theory for least squares series: pointwise and uniform results. Journal of Econometrics 186, 345–366.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M.D., & Titiunik, R. (2014) Robust nonparametric confidence intervals for regression-discontinuity designs. Econometrica, 82, 2295–2326.CrossRefGoogle Scholar
Cattaneo, M.D. & Farrell, M.H. (2013) Optimal convergence rates, Bahadur representation, and asymptotic normality of partitioning estimators. Journal of Econometrics, 174, 127–143.CrossRefGoogle Scholar
Chaudhuri, S. & Hill, J.B. (2016a) Heavy Tail Robust Estimation and Inference for Average Treatment Effects. Working paper.Google Scholar
Chaudhuri, S. & Hill, J.B. (2016b) Supplemental Appendix for “Robust Estimation for Average Treatment Effects” Part I. Working paper.Google Scholar
Chen, X. (2007) Large sample sieve estimation of semi-nonparametric models. In Heckman, J.J. & Leamer, E.E. (eds.), Handbook of Econometrics, vol. 6, 5549–5632. Elsevier.CrossRefGoogle Scholar
Chen, X. & Christensen, T.M. (2015) Optimal uniform convergence rates and asymptotic normality for series estimators under weak dependence and weak conditions. Journal of Econometrics 188, 447–465.CrossRefGoogle Scholar
Chen, X. & Liao, Z. (2014) Sieve M inference on irregular parameters. Journal of Econometrics 182, 70–86.CrossRefGoogle Scholar
Chen, X. & Pouzo, D. (2015) Sieve Wald and QLR inferences on semi/nonparametric conditional moment models. Econometrica 83, 1013–1079.CrossRefGoogle Scholar
Chernozhukov, V., Chetverikov, D., & Kato, K. (2014) Gaussian approximation of suprema of empirical processes. Annals of Statistics 42, 1564–1597.CrossRefGoogle Scholar
Crump, R.K., Hotz, V.J., Imbens, G.W., & Mitnik, O.A. (2009) Dealing with limited overlap in estimation of average treatment effects. Biometrika 96, 187–199.CrossRefGoogle Scholar
Csörgő, S., Haeusler, E., & Mason, D.M. (1988) The asymptotic distribution of trimmed sums. Annals of Probability, 16, 672–699.CrossRefGoogle Scholar
de Jong, R.M. (2002) A note on “Convergence rates and asymptotic normality for series estimators”: uniform convergence rates. Journal of Econometrics 111, 1–9.CrossRefGoogle Scholar
Dunbar, G., Lewbel, A., & Pendakur, K. (2017) Identification of Random Resource Shares in Collective Households Without Preference Similarity Restrictions. Working paper.Google Scholar
Eastwood, B.J. & Gallant, A.R. (1991) Adaptive rules for seminonparametric estimators that achieve asymptotic normality. Econometric Theory 7, 307–340.CrossRefGoogle Scholar
Escanciano, J.C. (2019) Semiparametric Identification and Fisher Information. Working paper.Google Scholar
Escanciano, J.C., Jacho-Chávez, D.T., & Lewbel, A. (2014) Uniform convergence of weighted sums of non and semiparametric residuals for estimation and testing. Journal of Econometrics 178, 426–443.CrossRefGoogle Scholar
Escanciano, J.C., Jacho-Chávez, D.T., & Lewbel, A. (2016) Identification and estimation of semiparametric two-step models. Quantitative Economics 7, 561–589.CrossRefGoogle Scholar
Fiorio, C.V., Hajivassiliou, V.A., and Phillips, P.C.B. (2010) Bimodal t-ratios: the impact of thick tails on inference. The Econometrics Journal 13, 271–289.CrossRefGoogle Scholar
Gallant, A.R. & Souza, G. (1991) On the asymptotic normality of Fourier flexible form estimates. Journal of Econometrics 50, 329–353.CrossRefGoogle Scholar
Graham, B.S. & Powell, J.L. (2012) Identification and estimation of average partial effects in "irregular" correlated random coefficient panel data models. Econometrica 80, 2105–2152.Google Scholar
Griffin, P.S. & Pruitt, W.E. (1987) The central limit problem for trimmed sums. Mathematical Proceedings of the Cambridge Philosophical Society 102, 329–349.CrossRefGoogle Scholar
Griffin, P.S. & Pruitt, W.E. (1989) Asymptotic normality and subsequential limits of trimmed sums. Annals of Probability 17, 1186–1219.CrossRefGoogle Scholar
Hansen, B.E. (2015) A Unified Asymptotic Distribution Theory for Parametric and Non-parametric Least Squares. Working paper.Google Scholar
Heiler, P. & Kazak, E. (2020) Valid inference for treatment effect parameters under irregular identification and many extreme propensity scores. Journal of Econometrics forthcoming.Google Scholar
Hill, J.B. & Renault, E. (2010) Generalized Method of Moments with Tail Trimming. Working paper.CrossRefGoogle Scholar
Hong, H., Leung, M.P., & Li, J. (2020) Inference on finite-population treatment effects under limited overlap. The Econometrics Journal 23, 32–47.CrossRefGoogle Scholar
Horvitz, D.G. & Thompson, D.J. (1952) A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association 47, 663–685.CrossRefGoogle Scholar
Huang, J.Z. (2003) Local asymptotics for polynomial spline regression. Annals of Statistics 31, 1600–1635.CrossRefGoogle Scholar
Khan, S. & Nekipelov, D. (2015) On Uniform Inference in Nonlinear Models with Endogeneity. Working paper.Google Scholar
Khan, S. & Tamer, E. (2010) Irregular identification, support conditions, and inverse weight estimation. Econometrica 78, 2021–2042.Google Scholar
Lewbel, A. (1997) Semiparametric estimation of location and other discrete choice moments. Econometric Theory 13, 32–51.CrossRefGoogle Scholar
Lewbel, A. (1998) Semiparametric latent variable model estimation with endogenous or mismeasured regressors. Econometrica 66, 105–121.CrossRefGoogle Scholar
Lewbel, A. (2000) Semiparametric qualitative response model estimation with unknown heteroscedasticity or instrumental variables. Journal of Econometrics 97, 145 – 177.CrossRefGoogle Scholar
Lewbel, A. (2014) An overview of the special regressor method. In Racine, J., Su, L., and Ullah, A. (eds.), The Oxford Handbook of Applied Nonparametric and Semiparametric Econometrics and Statistics, vol. 2, Oxford University Press.Google Scholar
Logan, B.F., Mallows, C., Rice, S., & Shepp, L.A. (1973) Limit distributions of self-normalized sums. Annals of Probability 1, 788–809.CrossRefGoogle Scholar
Ma, X. & Wang, J. (2020) Robust inference using inverse probability weighting. Journal of the American Statistical Association forthcoming.CrossRefGoogle Scholar
Newey, W.K. (1997) Convergence rates and asymptotic normality for series estimators. Journal of Econometrics 79, 147–168.CrossRefGoogle Scholar
Peña, V.H., Lai, T.L, & Shao, Q.-M. (2008) Self-Normalized Processes: Limit Theory and Statistical Applications, Springer Science & Business Media.Google Scholar
Peng, L. (2001) Estimating the mean of a heavy tailed distribution. Statistics & Probability Letters 52, 255–264.CrossRefGoogle Scholar
Peng, L. (2004) Empirical-likelihood-based confidence interval for the mean with a heavy-tailed distribution. Annals of Statistics 32, 1192–1214.CrossRefGoogle Scholar
Peng, L. & Qi, Y. (2017) Inference for Heavy-Tailed Data: Applications in Insurance and Finance, Academic Press.Google Scholar
Rajan, R.G. & Zingales, L. (1998) Financial dependence and growth. American Economic Review 88, 559–586.Google Scholar
Romano, J.P. & Wolf, M. (1999) Subsampling inference for the mean in the heavy-tailed case. Metrika 50, 55–69.CrossRefGoogle Scholar
Rosenbaum, P.R. & Rubin, D.B (1983) The central role of the propensity score in observational studies for causal effects. Biometrika 70, 41–55.CrossRefGoogle Scholar
Rothe, C. (2017) Robust confidence intervals for average treatment effects under limited overlap. Econometrica 85, 645–660.CrossRefGoogle Scholar
van de Geer, S. (1990) Estimating a regression function. Annals of Statistics 18, 907–924.Google Scholar
van de Geer, S. (2002) M-estimation using penalties or sieves. Journal of Statistical Planning and Inference 108, 55–69.CrossRefGoogle Scholar
Yang, S. & Ding, P. (2018) Asymptotic inference of causal effects with observational studies trimmed by the estimated propensity scores. Biometrika 105, 487–493.CrossRefGoogle Scholar
Yang, T.T. (2014) Asymptotic Trimming and Rate Adaptive Inference for Endogenous Selection Estimates. Working paper.Google Scholar